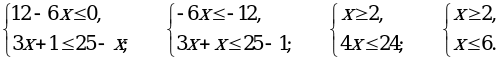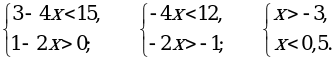Урок алгебры Дата:___06.04.2016____ Класс__8___
Тема урока: Решение систем неравенств с одной переменной
Цели урока:
| Учебные – формировать умения решения систем неравенств с одной переменной; умения планировать и контролировать ход своих действий при систем неравенств с одной переменной; повторить решение линейных неравенств; решения систем неравенств с одной переменной; закрепить умение решать системы неравенств с одной переменной;
|
| Развивающие – развивать логическое мышление, умение анализировать, обобщать; продолжить формирование математической речи, памяти, познавательной активности; развитие речи в ходе устных ответов и объяснений решений систем неравенств; развитие математической речи; коррекция речи учащихся в ходе обсуждения систем неравенств с одной переменной. Развивать коммуникативные способности учащихся (умение работать в парах, обучаться в сотрудничестве, вести монолог и диалог); Развивать умение наблюдать и систематизировать, добывать знания; логическое и теоретическое мышление; Совершенствовать вычислительные навыки. |
| Воспитательные - приучать к умению выслушивать других и умению общаться; продолжить воспитание у учащихся доброжелательности друг к другу; прививать чувство патриотизма. Работать над повышением грамотности устной и письменной речи учащихся; Воспитывать математическую культуру, интерес к предмету через разнообразие видов работы на уроке. |
Необходимо знать: алгоритм решения систем неравенств.
Необходимо уметь:
| - решать линейные неравенства и системы; - графически изображать множество их решений, а также записывать решения в виде числового промежутка; - производить отбор решений по заданному условию. |
Оборудование урока: доска, smartboard, опорный конспект, раздаточный материал
Тип урока: применения знаний и умений
Формы организации учебной деятельности: - фронтальная – коллективная - индивидуальная.
Методы: объяснительно – иллюстративный.
ПЛАН УРОКА
| Блоки | Этапы урока | Время |
| 1 | организационный момент проверка домашнего задания мотивация, совместная с учащимися постановка цели актуализация опорных знаний | 8 мин. |
| 2 | Основная часть: формирование умений и навыков осознание, осмысление первичное закрепление и применение нового материала работа в парах, работа в группах с применением само и взаимопроверки | 15 мин. |
| 3 | Активная физкультминутка вместе с учителем | 2 мин. |
| 4 | Работа по индивидуально – ориентированному плану плану | 13 |
| 5 | | 7 мин. |
ХОД УРОКА
I. Организационный момент.
Подтянулись, усмехнулись, гостям нашим улыбнулись! И начинаем работать с удовольствием и интересом.
II. Проверка домашнего задания.
Правильность выполнения.
Знание теоретического материала.
III. Актуализация опорных знаний.
Сегодня мы продолжаем с вами работать с системами неравенств. Наша цель продолжить знакомство с понятием системы неравенств с одной переменной, с алгоритмом её решения.
«Математика учит преодолевать трудности и исправлять собственные ошибки».
Задача: Автомобиль по горной дороге за 7 часов проезжает больше 210 км, а по шоссе за 5 часов – не более 400 км. В каких пределах может изменяться его скорость?
Составление системы неравенств по условию задачи.
Постановка проблем: требуется найти такие значения х, при которых верны оба неравенства, т.е. найти общее решение этих неравенств. В таких случаях говорят, что надо решить систему неравенств, и используют следующую запись
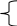 7х 210,
7х 210,
5х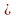 400.
400.
- Как вы думаете, что называется решением системы неравенств?
(Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы)
- Что значит « Решить систему неравенств»?
(Решить систему неравенств– значит найти все её решения или доказать, что решений нет)
- Что надо сделать, чтобы ответить на вопрос « является ли заданное число
решением системы неравенств?»
(Подставить это число в оба неравенства системы, если получатся верные неравенства, то заданное число является решением системы неравенств, если получатся неверные неравенства, то заданное число не является решение системы неравенств)
Решить самостоятельно систему в задаче на движение автомобиля и ответить на вопрос задачи.
Сформулировать алгоритм решения систем неравенств
Обобщаем теоретический материал, используя элементы технологии критического мышления (ВСЕ ПОЗНАЕТСЯ В СРАВНЕНИИ + методика МОЗГОВОГО ШТУРМА)
IV. Формирование умений и навыков.
4 учащихся (Кунгурова Соня, Гаврилюк Люда, Фирсенко Влада, Семикова Яна), которые опережают изучение программного материала, работают по индивидуально-ориентированному плану, остальные работают с учителем.
(Работа по плану, написанному на доске и одновременная актуализация
опорных знаний)
Вопросы к учащимся (и снова повторяем все вместе):
Что называется решением неравенства?
А как вы думаете, что называется решением системы неравенств?
Является ли число 5 решением данной системы? число 10?
Вывод (дают ребята, при затруднении помогает учитель).
Что значит решить неравенство?
А что значит решить систему неравенств?
Вывод
На какие свойства мы опираемся при решении неравенств?
Итак, как решаются системы неравенств с одной переменной?
Вывод:
а) решаем каждое из неравенств, записывая их одновременно под знаком системы
б) изображаем решение каждого неравенства на числовой прямой
в) находим пересечение (общее решение)
г) записываем ответ в виде числового промежутка или записи «решений нет»
Далее решается система записанная на доске и ещё раз проговаривается каждый пункт алгоритма решения.
С помощью системы неравенств удобно решать двойные неравенства.
-2≤ 2х+4≤6, но мы будем отрабатывать одновременный двусторонний алгоритм решения двойных неравенств.
3. Ответ-« образец» (даёт учитель).
4. Работа в парах (отработка теории).
5. Работа в группах (методика ВОЗ-взаимообмен заданиями)
Учащиеся распределяются учителем по две парты.
Работу в группах помогают контролировать 4 учащихся, которые идут с опережением и
учитель.
Каждый из 4 учащихся получает карточку, в которой 2 однотипных задания.
Оба задания ребёнок выполняет самостоятельно и сдаёт учителю. Затем ребята обмениваются карточками, проделывая аналогичную работу.
Карточка №1.
Решите систему неравенств:
а) { -2х≥ -4 б) { -2х≤8
3х≥21 6х≤18
Карточка №2
Решите двойное неравенство:
а) -3
Карточка №3:
Решите систему неравенств:
а){ 2х-16-2х
3х-2 х-4 4-2х
Карточка №4:
Решите систему неравенств:
а) {58-7х3х-2 б) { 25-6х
22х-131+4х
Карточка №5
Решите систему неравенств:
а) {7х+3≥5(х-4)+1 б) {5(х-2)-х≥2
4х+1≤43-3(7+х) 1+3(х+1)≤25
Карточка №6
Решите систему неравенств:
а) {х/3+х/4
1-х/60 2х-х/3≥1
В это время слабо мотивированные учащиеся (2 человека – Левочкин Роман и Капрова Аня) работают индивидуально, выполняют работу по образцу.
Физкультминутка.
Выполняем движения, используя помощника из интернета.
VI. Работа по ИОПу (индивидуально-ориентированному плану).
Каждый учащийся работает по своему плану. По необходимости получает консультацию учителя или товарища.
Дополнительные задачи:
задания сформулированы таким образом, что требуется не только найти решение системы, но проверить выполнение каких-либо дополнительных условий.
1. № 822 (б, г).
Р е ш е н и е
б) 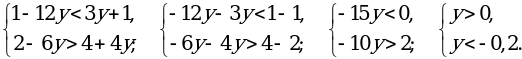
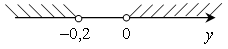 ;
; 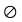 .
.
г) 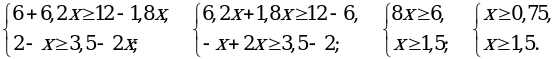
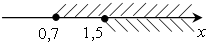 ; [1,5; +∞).
; [1,5; +∞).
О т в е т: б) нет решений; г) [1,5; +∞).
2. № 883 (б, г), № 884 (б).
Р е ш е н и е
№ 883.
б) Допустимы те значения переменной, при которых подкоренные выражения неотрицательны:
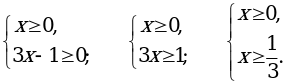
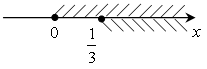 ;
; 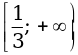 .
.
г) 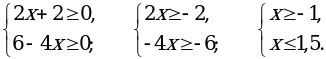
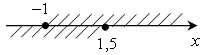 ; [–1; 1,5].
; [–1; 1,5].
О т в е т: б) 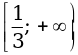 ; г) [–1; 1,5].
; г) [–1; 1,5].
№ 884.
б) В область определения функции y = 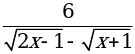 входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
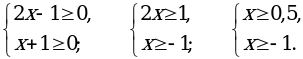

Знаменатель равен нулю, если:
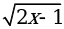 =
=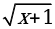 ;
;
2х – 1 = х + 1;
2х – х = 1 + 1;
х = 2.
Значит, из области определения функции необходимо исключить х = 2.
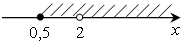 ; [0,5; 2)
; [0,5; 2) 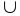 (2; +∞).
(2; +∞).
О т в е т: [0,5; 2) 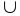 (2; +∞).
(2; +∞).
3. № 886 (б, г).
Р е ш е н и е
б) 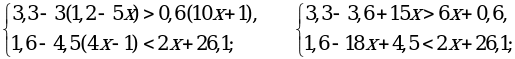
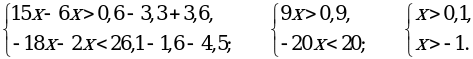
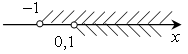 ; (0,1; +∞).
; (0,1; +∞).
г) 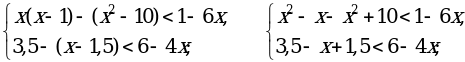
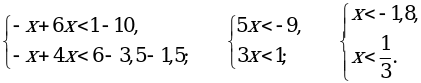
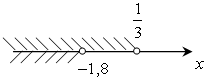 ; (–∞; –1,8).
; (–∞; –1,8).
О т в е т: б) (0,1; +∞); г) (–∞; –1,8).
4. № 887 (б, г).
Р е ш е н и е
б) 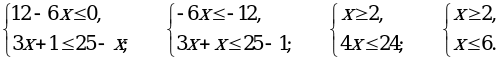
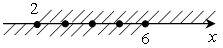 ; [2; 6].
; [2; 6].
Целыми решениями являются: 2; 3; 4; 5; 6.
г) 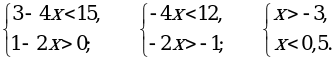
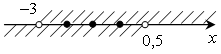
Целыми решениями являются: –2; –1; 0.
О т в е т: б) 2; 3; 4; 5; 6; г) –2; –1; 0.
VII. РЕФЛЕКСИЯ
Продолжите предложение:
Сегодня на уроке мне понравилось …
Сегодня на уроке я узнал …
Сегодня на уроке мне было сложно…
Я хотел, чтобы на следующем уроке …
VIII. Подведение итогов и обобщение изученного материала
Что является решением системы неравенств с одной переменной?
Что значит решить систему неравенств с одной переменной?
Рассказать алгоритм решения систем неравенств с одной переменой.
IX. Домашнее задание1. §35, выучить правила
2. выучить алгоритм, записанный в тетради
3. №873
4. по желанию №876.
8







 7х 210,
7х 210, 400.
400.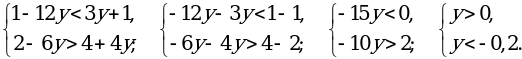
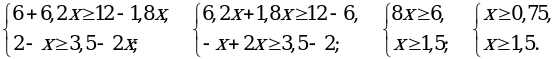
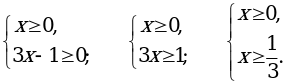
 ;
; 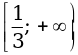 .
.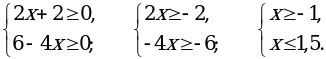
 ; [–1; 1,5].
; [–1; 1,5].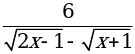 входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.
входят те значения х, для которых подкоренные выражения неотрицательны и знаменатель дроби не обращается в нуль.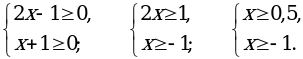

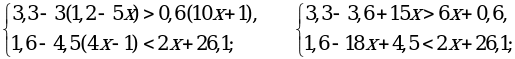
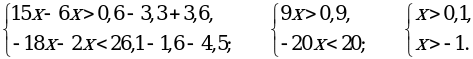
 ; (0,1; +∞).
; (0,1; +∞).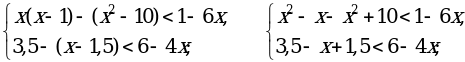
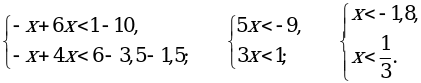
 ; (–∞; –1,8).
; (–∞; –1,8).