Тема. Тригонометрические уравнения и методы их решения
План занятия:
-
Простейшие тригонометрические уравнения
-
Методы решения тригонометрических уравнений с примерами
-
Самостоятельная работа
Простейшие тригонометрические уравнения
-
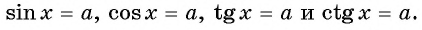 при 0a|
при 0a|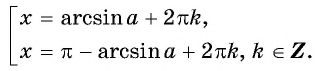
При 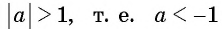 или
или 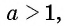 уравнение
уравнение 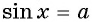 не имеет корней, так как множеством значений функции
не имеет корней, так как множеством значений функции
-
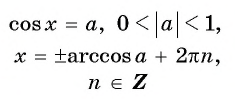
При 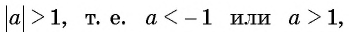 уравнение
уравнение 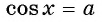 не имеет корней, так как множеством значений функции
не имеет корней, так как множеством значений функции 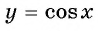 является промежуток
является промежуток 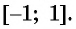
-
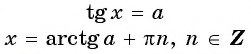 4.
4. 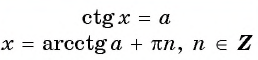
Частные случаи
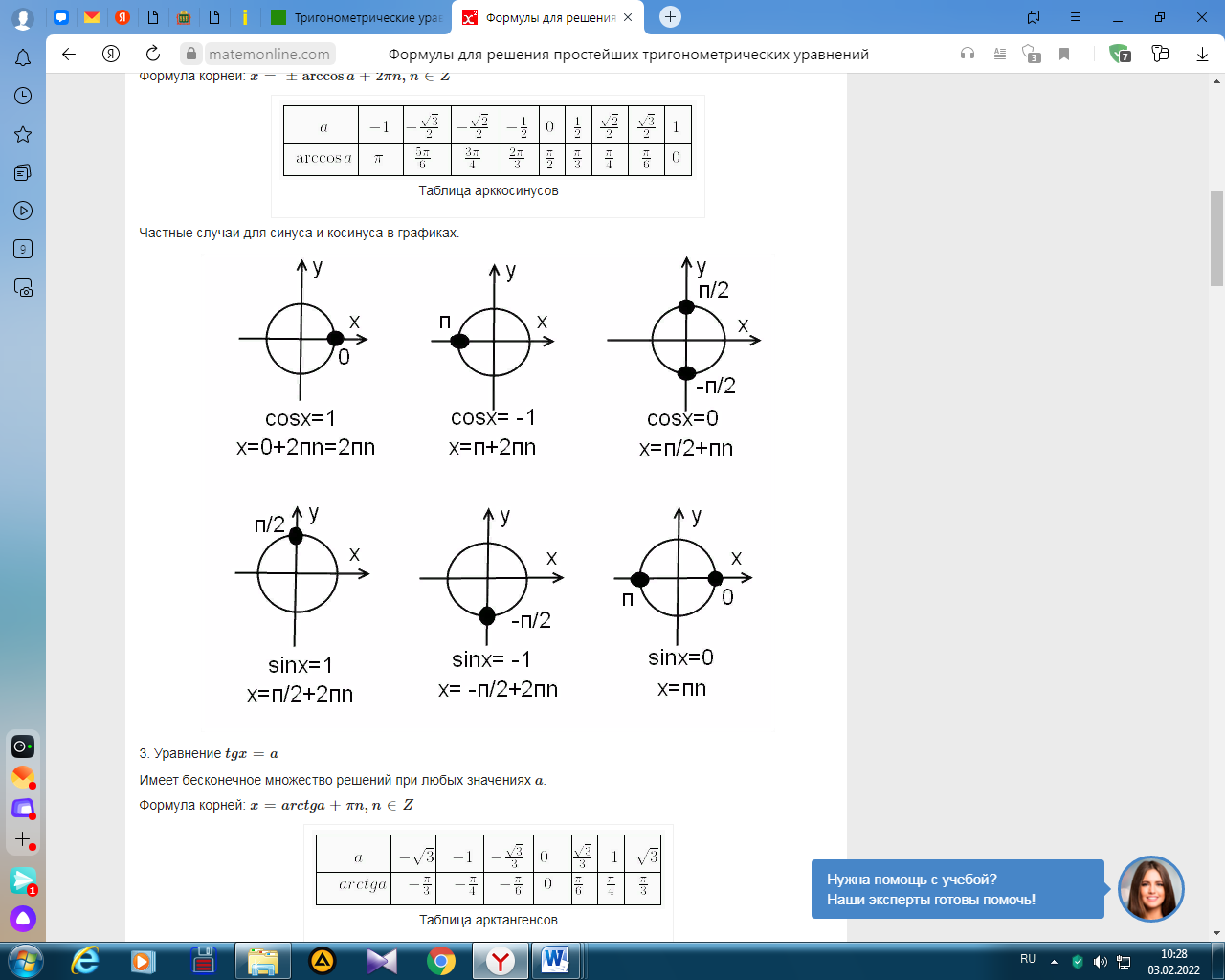
Методы решения тригонометрических уравнений
1.Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.
Сформулируем алгоритм решения уравнений методом введения новой переменной.
1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.
2. Обозначить полученную функцию переменной t .
3. Записать и решить полученное алгебраическое уравнение.
4. Сделать обратную замену.
5. Решить простейшее тригонометрическое уравнение.
Пример 1.
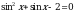
Введем замену: 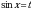 , тогда получаем уравнение
, тогда получаем уравнение 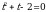 .
.
Решим его: 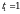 ,
, 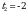 .
.
Возвращаем замену переменных:
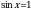 , решение этого уравнения имеет вид:
, решение этого уравнения имеет вид: 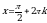 ,
, 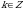 .
.
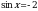 , это уравнение не имеет корней, так как правая часть должна принадлежать отрезку
, это уравнение не имеет корней, так как правая часть должна принадлежать отрезку 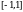 . А -2 не входит в этот отрезок.
. А -2 не входит в этот отрезок.
Ответ: 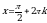 ,
, 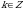 .
.
Пример 2.
Решим уравнение
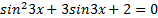
Решение:
Заметим, что левая часть уравнения представляет собой выражение, которое зависит от 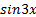 , поэтому в качестве новой переменной мы можем выбрать
, поэтому в качестве новой переменной мы можем выбрать 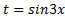 .
.
После введения новой переменной мы получим уравнение:
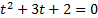
Решим его:
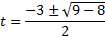 ,
, 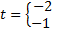
Первое из полученных простейших уравнений 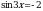 решений не имеет.
решений не имеет.
Решим второе уравнение: 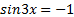 .
.
Решение этого простейшего уравнения имеет вид 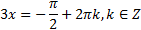 .
.
То есть  .
.
Ответ:  .
.
2-й Метод решения тригонометрических уравнений 1-го и 2-го порядка
Однородными уравнениями первого и второго порядка называются уравнения вида:
 соответственно (а ≠ 0, b ≠ 0, с ≠ 0 ).
соответственно (а ≠ 0, b ≠ 0, с ≠ 0 ).
При решении однородных уравнений почленно (каждое слагаемое) делят обе части уравнения на cosx для (1) уравнения и на cos2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.
Пример 3.
Рассмотрим уравнении: 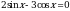 - 1-го порядка
- 1-го порядка
Это уравнение имеет разные функции sin и cos, поэтому мы можем поделить все уравнение или на sinх или на cosх
Разделим уравнение на sinx, тогда:
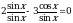
2-3ctgx=0
Перенесем число 2 в правую часть с противоположным знаком:
-3ctgx=-2
Поделим обе части уравнения на -3:

Решим полученное уравнение: 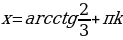 ,
, 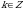 .
.
Пример 4.
Решить уравнение:
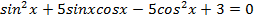
Решение:
Сначала умножим 3 на тригонометрическую единицу, то есть на выражение
(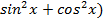 . Мы получим:
. Мы получим:
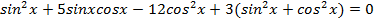
Теперь преобразуем полученное уравнение к однородному виду, раскрыв скобки:
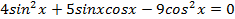
Разделим полученное уравнение на cos2x каждое слагаемое, в итоге получим tgx
Теперь решим полученное однородное уравнение:
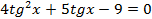
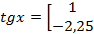 .
.
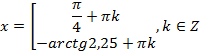 .
.
Ответ: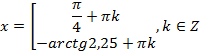 .
.
Самостоятельная работа
-
Переписать всю лекцию вместе с примерами, разобрать решение каждого примера. Прислать фото. Не переписывать только первый пункт – Простейшие тригонометрические уравнения. Они есть у вас в тетрадях
-
Решить следующие уравнения и прислать фото
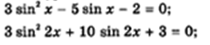
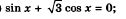
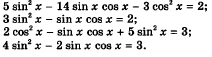







 4.
4. 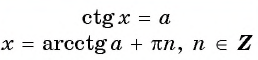

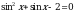
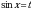 , тогда получаем уравнение
, тогда получаем уравнение 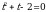 .
.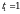 ,
, 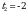 .
.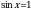 , решение этого уравнения имеет вид:
, решение этого уравнения имеет вид: 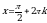 ,
, 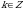 .
.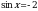 , это уравнение не имеет корней, так как правая часть должна принадлежать отрезку
, это уравнение не имеет корней, так как правая часть должна принадлежать отрезку 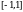 . А -2 не входит в этот отрезок.
. А -2 не входит в этот отрезок.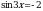 решений не имеет.
решений не имеет.  соответственно (а ≠ 0, b ≠ 0, с ≠ 0 ).
соответственно (а ≠ 0, b ≠ 0, с ≠ 0 ). 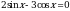 - 1-го порядка
- 1-го порядка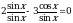

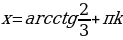 ,
, 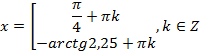 .
.


















