-
В горизонтально расположенной трубке постоянного сечения, запаянной с одного конца, помещён столбик ртути длиной 7,5 см, который отделяет воздух в трубке от атмосферы. Трубку расположили вертикально, запаянным концом вниз. На сколько градусов следует нагреть воздух в трубке, чтобы объём, занимаемый воздухом, стал прежним? Температура воздуха в лаборатории 300 К, а атмосферное давление составляет 750 мм рт. ст..
| Дано: | Решение: |
| Т1 = 300 К, lрт = 7,5 см, р0 = 750 мм рт.ст. Найти: ΔТ
| Уравнение Клапейрона для воздуха в трубке 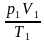 = = 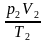 . По условию объем воздуха в горизонтальной и вертикальной трубке V1 = V2, температура воздуха в трубке, расположенной вертикально T2 = T1 + ΔТ, столбик ртути в горизонтальной трубке в равновесии, поэтому давление воздуха в трубке p1 = p0. . По условию объем воздуха в горизонтальной и вертикальной трубке V1 = V2, температура воздуха в трубке, расположенной вертикально T2 = T1 + ΔТ, столбик ртути в горизонтальной трубке в равновесии, поэтому давление воздуха в трубке p1 = p0. Так как столбик ртути в вертикально расположенной трубке покоится, то давление воздуха p2 = p0 + pрт. Подставим значения макропараметров воздуха в уравнение Клапейрона 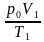 = = 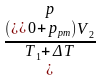 . Выразим ΔТ. . Выразим ΔТ. р0 (T1 + ΔТ) = (p0 + pрт) T1, р0 T1 + р0ΔТ = p0 T1 + pрт T1, ΔТ = 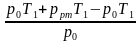 , ΔТ = , ΔТ = 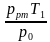 = = 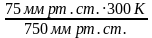 = 30 К. = 30 К. Ответ: на 30 К. |
-
В калориметре находятся в тепловом равновесии 50 г воды и 5 г льда. Какой должна быть минимальная масса болта, имеющего удельную теплоёмкость 500 Дж/(кг ⋅ К) и температуру 339 К, чтобы после опускания его в калориметр весь лёд растаял? Тепловыми потерями пренебречь.
| Дано: | Решение: |
| m1 = 50 г, m2 = 5 г, Т 3= 339 К, c 3= 500 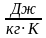 , , λ = 330000 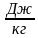 Найти: m3 | Определим количество теплоты, необходимое для плавления льда Q2 = λ∙ m2. Рассчитаем количество теплоты, которое выделит болт при охлаждении Q1 = c 3 ∙ m3 (Т 3 - Т), где Т - температура теплового равновесия воды и льда, Т = 273 К. По условию Q2 = Q1, λ∙ m2 = c 3 ∙ m3 (Т 3 - Т). Выразим массу болта. m3 = 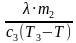 , m3 = , m3 = 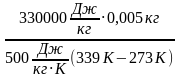 = 0,05 кг = 50 г. = 0,05 кг = 50 г. Ответ: 50 г. |
-
Установите соответствие между процессами, в которых участвует 1 моль одноатомного идеального газа, и физическими величинами (ΔU – изменение внутренней энергии; А – работа газа), которые их характеризуют. К каждой позиции первого столбца подберите соответствующую позицию
из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами. |
| | | ПРОЦЕССЫ | ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | | А) | адиабатное расширение | | Б) | изотермическое сжатие |
| | 1) | ΔU = 0; A 0 | | 2) | ΔU = 0; A | | 3) | ΔU A 0 | | 4) | ΔU 0; A |
|
|
Решение. 1. Адиабатный процесс протекает без теплообмена с окружающей средой Q = 0. Первый закон термодинамики для адиабатного процесса ΔU = - А. Газ расширяется, объем увеличивается, он совершает положительную работу А 0, из первого закона термодинамики следует, что его внутренняя энергия уменьшается ΔU
2. Изотермический процесс протекает при постоянной температуре, следовательно, внутренняя энергия газа не изменяется U =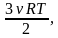 ΔU = 0. Первый закон термодинамики для изотермического процесса Q = А. Газ сжимается, объем газа уменьшается, значит A Для Б) верен вариант 2
ΔU = 0. Первый закон термодинамики для изотермического процесса Q = А. Газ сжимается, объем газа уменьшается, значит A Для Б) верен вариант 2
Ответ: 32.
-
Тепловая машина с максимально возможным КПД имеет в качестве нагревателя открытый сверху резервуар с кипящей водой, а в качестве холодильника – сосуд со льдом при 0 °С. Атмосферное давление равно 105 Па. Какая масса льда растает при совершении машиной работы 1 МДж? Ответ в кг округлите до десятых.
| Дано: | Решение: |
| T1 = 373 К, T2 = 273 К, p = 105 Па, А = 1 МДж, λ = 3,3 ∙ 105 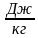 Найти: mл | КПД идеальной машины: η=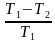 или η = или η =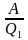 , Q1 = Q2 + A, количество теплоты, отданное холодильнику Q2 = λmл. , Q1 = Q2 + A, количество теплоты, отданное холодильнику Q2 = λmл. 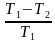 = =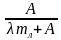 , , 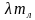 ( (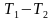 ) ) 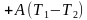 = =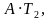 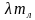 ( (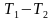 ) = ) = 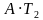 , , 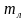 = =  . . 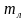 = ≈ 8,3 кг. = ≈ 8,3 кг.
Ответ: ≈ 8,3 кг. |
-
На рисунке изображена диаграмма четырёх последовательных изменений состояния 2 моль идеального газа. В каком процессе работа газа имеет положительное значение и максимальна по величине, а в каком работа внешних сил положительна и минимальна по величине?
Установите соответствие между этими процессами и номерами процессов на диаграмме.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| | | ПРОЦЕСС | | НОМЕР ПРОЦЕССА | | А) | работа газа положительна и максимальна | | Б) | работа внешних сил положительна и минимальна |
| |
|
|
Решение. Работа газа и над газом численно равна площади фигуры под графиком зависимости p(V). Газ совершает положительную работу, если объем газа увеличивается, внешние силы совершают положительную работу, если объем газа уменьшается.
Ответ: 14.
-
При переходе 2 моль идеального газа из состояния 1 в состояние 2 давление газа
| | 1) | сначала увеличивается, потом уменьшается |
| | 2) | не изменяется |
| | 3) | уменьшается |
| | 4) | увеличивается |
Решение. Мысленно через точки 1 и 2 проведем изобары ( = const,
= const,  = const). Чем ниже расположена изобара (угол наклона к оси оТ меньше), тем большее ей соответствует давление.
= const). Чем ниже расположена изобара (угол наклона к оси оТ меньше), тем большее ей соответствует давление.
Ответ: 4.
-
Переход вещества из жидкого состояния в твёрдое при температуре его кристаллизации сопровождается |
| | 1) | увеличением кинетической энергии теплового движения молекул вещества | | | 2) | увеличением энергии взаимодействия молекул вещества | | | 3) | уменьшением энергии взаимодействия молекул вещества | | | 4) | уменьшением кинетической энергии теплового движения молекул вещества |
|
Решение. Кинетическая энергия теплового движения молекул вещества зависит от температуры. Температура не меняется, следовательно, кинетическая энергия теплового движения молекул вещества остается неизменной. Так как при кристаллизации тепло выделяется, внутренняя энергия вещества уменьшается, значит, уменьшается энергия взаимодействия молекул вещества.
Ответ: 3.
-
В горизонтальном цилиндре с гладкими стенками под массивным поршнем с площадью S находится одноатомный идеальный газ. Поршень соединён с основанием цилиндра пружиной с жёсткостью k. В начальном состоянии расстояние между поршнем и основанием цилиндра равно L, а давление газа в цилиндре равно внешнему атмосферному давлению р0 (см. рисунок). Какое количество теплоты Q передано затем газу, если в результате поршень медленно переместился вправо на расстояние b?
Решение.
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной. В процессе медленного движения поршня его ускорение считаем ничтожно малым. Поэтому сумма приложенных к поршню сил при его движении равна нулю.
В проекциях на горизонтальную ось х получаем:
 ,
,
где F0 – сила давления атмосферы на поршень, F1 – сила давления газа в цилиндре на поршень, Fупр – упругая сила, действующая на поршень со стороны пружины.
2. Из равенства давлений слева и справа от поршня в начальном состоянии и гладкости стенок следует, что в начальном состоянии пружина не деформирована. Поэтому при смещении поршня вправо от начального положения на величину х модуль упругой силы  . Тогда
. Тогда

и давление в цилиндре при смещении поршня вправо от начального положения на величину х равно  (см. график на рисунке б).
(см. график на рисунке б).
3. Из модели одноатомного идеального газа

следует:
 .
.
Внутренняя энергия газа в исходном состоянии равна  , а в конечном состоянии
, а в конечном состоянии
.
4. Из первого начала термодинамики получаем:  . Работа газа А12 при сдвиге поршня из начального в конечное состояние равна произведению величины S и площади трапеции под графиком р(х) на рис. б:
. Работа газа А12 при сдвиге поршня из начального в конечное состояние равна произведению величины S и площади трапеции под графиком р(х) на рис. б:
.
Подставляя в выражение для Q значения U1, U2 и А12, получим:
Ответ:  .
.
-
В тепловом двигателе 1 моль одноатомного разреженного газа совершает цикл 1–2–3–4–1, показанный на графике в координатах p–T, где p – давление газа, Т – абсолютная температура. Температуры в точках 2 и 4 равны и превышают температуру в точке 1 в 2 раза. Определите КПД цикла.
| Дано: | Решение: |
| T2 = T4 = 2T1, p = 105 Па, ν = 1 моль, Найти: η | Процесс 1 - 2: V1 = V2,  = = , T2 = 2T1, p2 = 2p1. , T2 = 2T1, p2 = 2p1. Процесс 2 - 3: p3 = p2 = 2p1,  = =  . . Процесс 3 - 4: V3 = V4 ,  = = . . Процесс 4 - 1: p4 = p1,  = =  , T4 = 2T1, V4 = 2V1, V3 = V4 = 2V1. , T4 = 2T1, V4 = 2V1, V3 = V4 = 2V1. 
p Построим этот цикл в координатах p(V): 
  
2 3 P2
   
   
4 P1
  
  
2V1 V1 V
Работа газа численно равна площади прямоугольника в координатах p(V): A = (p2 – p1)( V2 – V1) = p1 V1 = ν R T1. Количество теплоты, полученное газом от нагревателя: Q = Q12 + Q23. Согласно первому закону термодинамики Q12 = ΔU12 + А =  - -  , , Q23 = ΔU23 + А23 =  - -  + 2p1 (2V1 - V1). Подставляем в формулу для Q и упрощаем выражение. Используем уравнение Менделеева-Клапейрона pV = ν RT . + 2p1 (2V1 - V1). Подставляем в формулу для Q и упрощаем выражение. Используем уравнение Менделеева-Клапейрона pV = ν RT . Q =  - -  + 2p1V1 = + 2p1V1 =  (p3V3 – p1V1) + 2p1V1 = (p3V3 – p1V1) + 2p1V1 = (2p12V1 – p1V1) + 2p1V1 = (2p12V1 – p1V1) + 2p1V1 =  3p1V1 + 2p1V1 = 6,5 p1V1. 3p1V1 + 2p1V1 = 6,5 p1V1. КПД теплового двигателя: η = ∙100%, η = ∙100%, η = ∙100% ≈ 15,4%. ∙100% ≈ 15,4%. Ответ: ≈ 15,4%. |
-
Стеклянный сосуд, содержащий влажный воздух при t1 = 30 °С, плотно закрыли крышкой и нагрели до t2= 50 °С. Опираясь на законы молекулярной физики, объясните, как изменятся при этом парциальное давление водяного пара и относительная влажность воздуха в сосуде.
Решение. Объем пара постоянный V = const, из закона Шарля следует  =
= , т.к. температура пара повысилась T2 T1, то p2 p1, парциальное давление пара р увеличилось.
, т.к. температура пара повысилась T2 T1, то p2 p1, парциальное давление пара р увеличилось.
Относительная влажность воздуха в сосуде определяется по формуле φ1 = * 100%, φ1 =
* 100%, φ1 = * 100%, плотность насыщенного водяного пара увеличилась с увеличением температуры ρ02 ρ01, абсолютная влажность ρ =
* 100%, плотность насыщенного водяного пара увеличилась с увеличением температуры ρ02 ρ01, абсолютная влажность ρ =  не изменилась, т.к. масса водяного пара и объем не изменились. Следовательно, относительная влажность воздуха в сосуде уменьшилась.
не изменилась, т.к. масса водяного пара и объем не изменились. Следовательно, относительная влажность воздуха в сосуде уменьшилась.






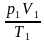 =
= 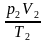 . По условию объем воздуха в горизонтальной и вертикальной трубке V1 = V2, температура воздуха в трубке, расположенной вертикально T2 = T1 + ΔТ, столбик ртути в горизонтальной трубке в равновесии, поэтому давление воздуха в трубке p1 = p0.
. По условию объем воздуха в горизонтальной и вертикальной трубке V1 = V2, температура воздуха в трубке, расположенной вертикально T2 = T1 + ΔТ, столбик ртути в горизонтальной трубке в равновесии, поэтому давление воздуха в трубке p1 = p0.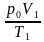 =
= 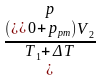 . Выразим ΔТ.
. Выразим ΔТ.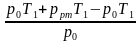 , ΔТ =
, ΔТ = 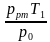 =
= 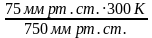 = 30 К.
= 30 К.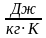 ,
,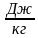
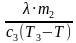 , m3 =
, m3 = 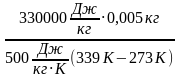 = 0,05 кг = 50 г.
= 0,05 кг = 50 г. ΔU = 0. Первый закон термодинамики для изотермического процесса Q = А. Газ сжимается, объем газа уменьшается, значит A Для Б) верен вариант 2
ΔU = 0. Первый закон термодинамики для изотермического процесса Q = А. Газ сжимается, объем газа уменьшается, значит A Для Б) верен вариант 2 или η =
или η =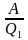 , Q1 = Q2 + A, количество теплоты, отданное холодильнику Q2 = λmл.
, Q1 = Q2 + A, количество теплоты, отданное холодильнику Q2 = λmл.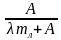 ,
, 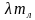 (
(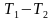 )
) 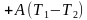 =
=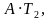
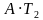 ,
, 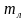 =
= 


















