Решение задач ОГЭ на сплавы и смеси

Методы решения различных типов задач «сплавы и смеси» (№ 22 ОГЭ, №11 ЕГЭ)

учитель математики Михайлова Ж.В.

При решении текстовых задач могут помочь несколько простых и общих советов:

• Прочитайте и тщательно изучите условие задачи.
• Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.
• Выбор неизвестных.
• Составление и решение «математической модели». (При составлении «математической модели» (уравнения, неравенства, системы уравнений или неравенств) еще раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый «знак» полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
• Решить полученное уравнение, систему, неравенство. (Если решение задачи не получается, то нужно еще раз прочитать и проанализировать задачу.)

Задача 1.

Два велосипедиста одновременно отправились в 153-километровый пробег. Первый ехал со скоростью на 8 км/ч больше, чем скорость второго, и прибыл к финишу на 8 часов раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

Решение. Пусть х км/ч скорость второго велосипедиста, тогда согласно условию задачи, составим таблицу:

Расстояние(км)

1 велосип.

Скорость ( км/ч)

2 велосип.

153

Время

х+8

153

(ч)

153/(х+8)

х

153/х

Зная, что второй велосипедист был в пути на 8 часов больше, чем первый, составим и решим уравнение

= 9

= -17, что не удовлетворяет условию задачи

Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту? Решение: Пусть за минуту в бак накачивается  х  литров воды.

Объем

накачать

117

За минуту

выкачать

Время

х

96

117/х

х+3

96/(х+3)

По условию задачи составим уравнение:

х≠0, х≠-3

117(х+3)-96х=5х(х+3)

117х+351-96х=5 +15х

• - 6х - 351=0

х=9 и х = -7,8( не удовлетворяет условию задачи)

Ответ: 9 литров.

Пример№1:

Определить концентрацию раствора, полученного при слиянии 150 г 30%-го и 250 г 10% го растворов какой-либо соли.

Дано:

m1=150г

m2=250г

Пусть концентрация полученного раствора х %

30 %

Х % - 10%

150 г

3

=

Х %

ω 1 =30 %

ω 2 =10 %

Найти ω 3

5

30%-х%

250 г

10 %

Отношение разностей массовых долей равно отношению масс растворов:

Х-10

Х= 17,5

3

=

30-х

5

Ответ: 17, 5%

Пример №2.

Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?

Свинец Медь

Свинец Медь

Свинец Медь

+

=

15%

65%

30%

200 г

(200 – Х) г

Х г

0,15Х + 0,65(200 – Х) = 0,3 * 200

Х = 140 (г) – первый сплав

200 – Х = 200 – 140 = 60 (г) – второй сплав

Ответ: 140г, 60г.

Таблица для решения задач имеет следующий вид

Наименование

веществ, растворов,

% содержание

вещества (доля

Масса

смесей, сплавов

раствора

Масса

содержания

вещества)

вещества

(смеси, сплава)

Задача 1 . Смешали 4 л 15%-ного раствора соли с 5 л 20%-ного соли к смеси добавили 1 л чистой воды. Какова концентрация полученной смеси?

Наименование

I раствор

веществ, смесей

% содержание

(доля) вещества

15 % = 0,15

Масса

II раствор

раствора (л)

Масса

4

20 % = 0,2

вода

вещества(л)

0%

0,15·4

Смесь

5

1

0,2·5

х % = 0,01х

0

10

0,01х·10

Уравнение для решения задачи имеет вид:

0,15·4 + 0,2·5=0,01х·10

0,1х = 1,6

х = 16

Ответ: концентрация смеси 16 %.

Задача 2. Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 %раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 %растворов кислоты было смешано?

Наименование

веществ, смесей

I раствор

% содержание (доля) вещества

II раствор

40 % = 0,4

Масса

Масса

раствора (кг)

15 % = 0,15

Вода

х

вещества (кг)

Смесь I

0,4х

у

0%

20 % = 0,2

3

0,15у

0%

х + у +3

0,2(х + у +3)

Кислота

80 % = 0,8

Смесь II

3

50 % = 0,5

0,8·3

х + у +3

0,5(х + у +3)

Для решения задачи получаем систему уравнений:

Ответ:3,4 кг 40 % кислоты и 1,6 кг 15 % кислоты.

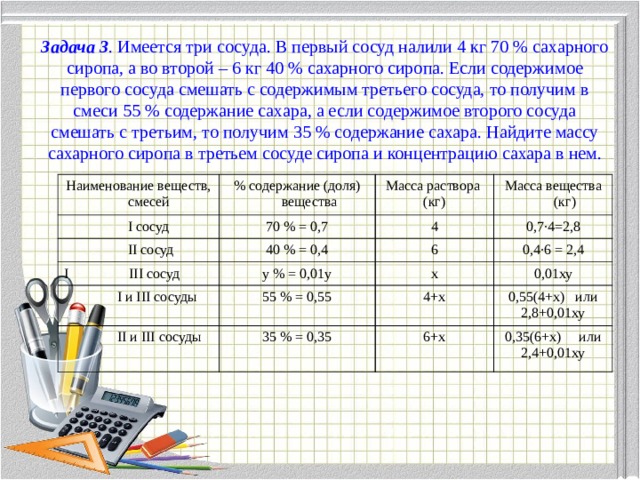
Задача 3 . Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного сиропа в третьем сосуде сиропа и концентрацию сахара в нем.

Наименование веществ, смесей

% содержание (доля) вещества

I сосуд

70 % = 0,7

II сосуд

Масса раствора

40 % = 0,4

I III сосуд

Масса вещества (кг)

(кг)

4

0,7·4=2,8

у % = 0,01у

I и III сосуды

6

0,4·6 = 2,4

х

55 % = 0,55

II и III сосуды

0,01ху

35 % = 0,35

4+х

0,55(4+х) или

6+х

2,8+0,01ху

0,35(6+х) или

2,4+0,01ху

Итак, получаем систему уравнений :

Решаем её:

Ответ :1,5 кг сахарного сиропа 15 % концентрации.

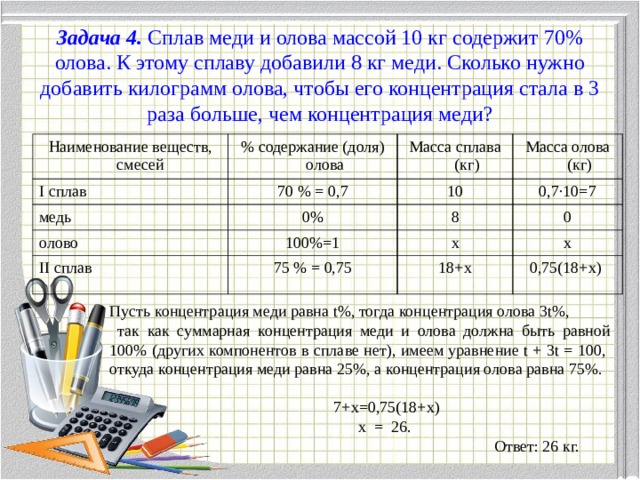
Задача 4. Сплав меди и олова массой 10 кг содержит 70% олова. К этому сплаву добавили 8 кг меди. Сколько нужно добавить килограмм олова, чтобы его концентрация стала в 3 раза больше, чем концентрация меди?

Наименование веществ, смесей

% содержание (доля) олова

I сплав

70 % = 0,7

Масса сплава (кг)

медь

олово

Масса олова (кг)

10

0%

100%=1

0,7·10=7

8

II сплав

0

х

75 % = 0,75

х

18+х

0,75(18+х)

Пусть концентрация меди равна t%, тогда концентрация олова 3t%,

так как суммарная концентрация меди и олова должна быть равной 100% (других компонентов в сплаве нет), имеем уравнение t + 3t = 100, откуда концентрация меди равна 25%, а концентрация олова равна 75%.

7+х=0,75(18+х)

  х  =  26.

Ответ: 26 кг.

Предлагаемый подход к решению текстовых задач с помощью уравнений сводится к следующему: 1.Через х обозначаем меньшую величину или то, о чём спрашивается в вопросе задачи. 2.Краткую запись оформляем в виде таблицы, схемы. 3.По условию задачи заполняем 2 столбика задачи, третий столбик нам даёт уравнение. 4.Смотрим, к какому типу относится задача (на сложение величин, на сравнение и т.п.) в зависимости от этого составляем уравнение. 5.Найдя х, смотрим, ответили мы на вопрос задачи, или нет, если нет, то решаем и находим ответ.

Спасибо за внимание!