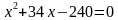Дата:
Тема: Решение задач по теме «Вписанная и описанная окружности»
Задачи: продолжить формирование навыков решения задач по теме.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.
Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.
Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.
Для любого треугольника:
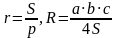
Для равностороннего треугольника.
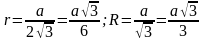
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.
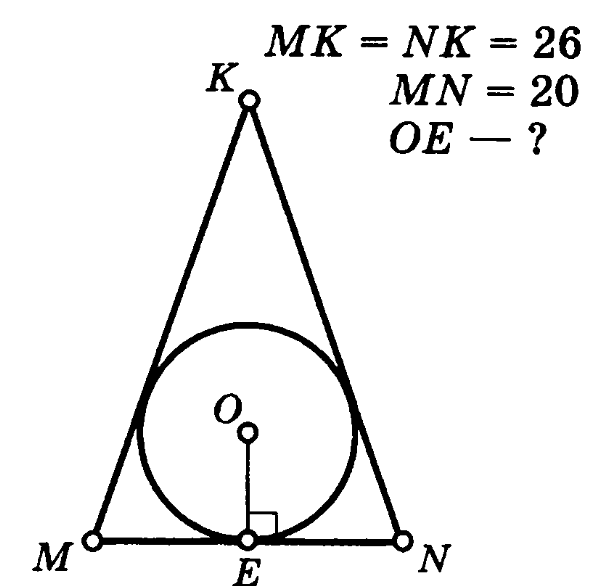
Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 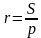 , где р – полупериметр.
, где р – полупериметр.
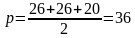
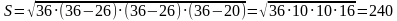
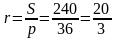
Ответ: 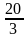 .
.
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.
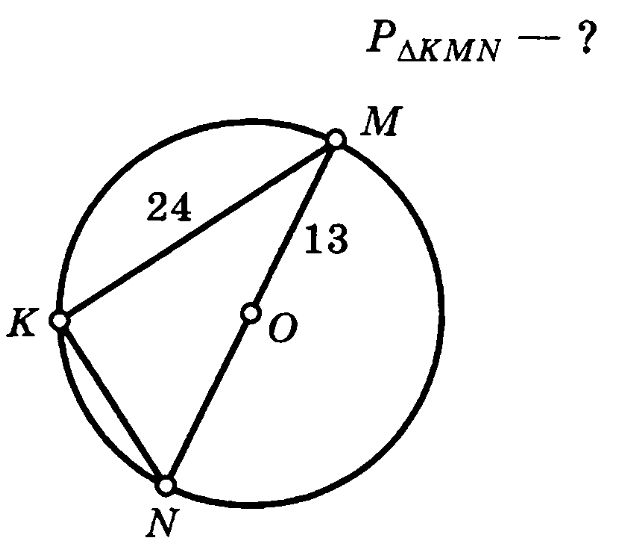
Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.
Ответ: 60.
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.
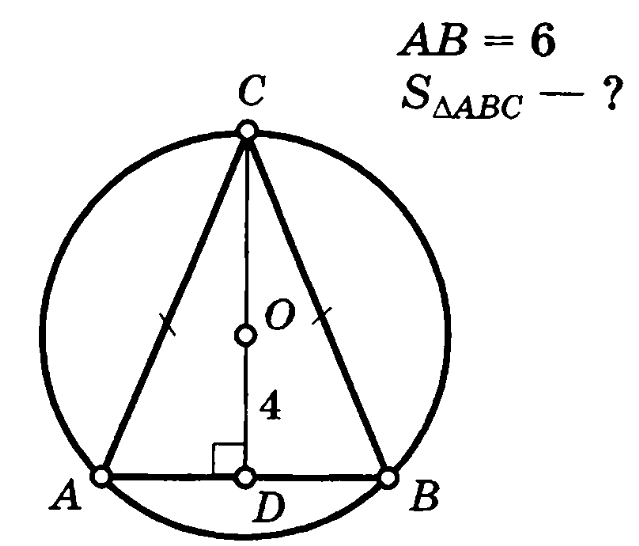
Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.
Ответ: 27.
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.
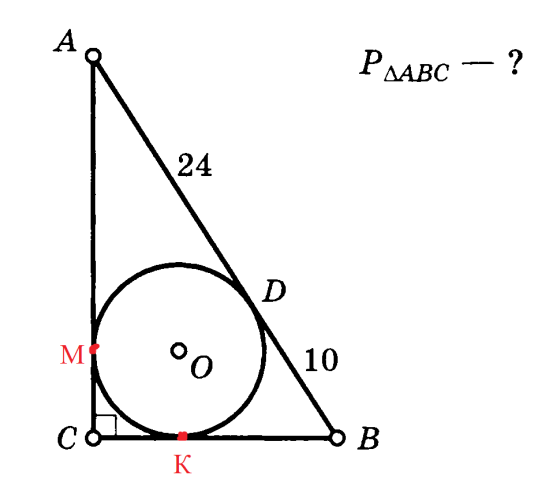
Решение (краткое). DB=DK=10, AD=AM=24.
KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.
Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.
По теореме Пифагора:
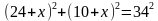
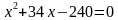
х=6
KC=CM=х=6.
РАВС=AD+DB+BK+KC+CM+MA=24+10+10+6+6+24=80.
Ответ: 80.
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание.
№1.
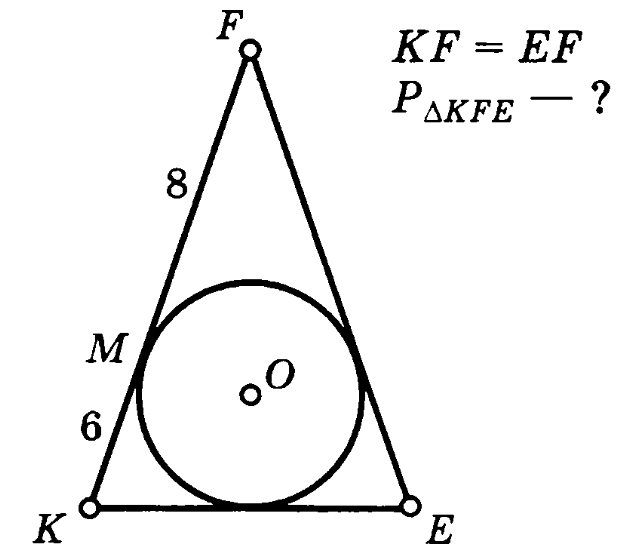





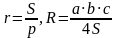
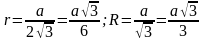

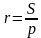 , где р – полупериметр.
, где р – полупериметр.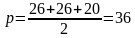
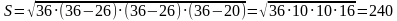
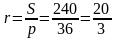
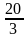 .
.