Урок геометрии в 9 классе по теме: Решение задач о вписанных и описанных многоугольниках

Урок геометрии в 9 классе №38 от 31.01.19 .

Тема урока: Решение задач по теме: вписанные и описанные многоугольники

Цели урока:

образовательная:

- Повторить и обобщить основные сведения о вписанных и описанных многоугольниках. Продолжить работу по подготовке к ОГЭ.

-Совершенствовать навыки решения задач и на применение теорем о вписанных и описанных многоугольниках , вписанных и центральных углах, а формул для радиусов вписанных и описанных окружностей треугольников.

развивающая: Развивать логическое мышление,  внимание; развивать приемы мыслительной деятельности: анализ, синтез, сравнение, обобщение, классификация; развивать математическую речь

Показать применение данной темы при решении задач с практическим содержанием., формировать критическую оценку своей деятельности , а также развивать у учащихся пространственное воображение.

воспитательная : воспитывать навыки самоконтроля, привычки к рефлексии; добиваться изменения роли ученика в учебном процессе от пассивного наблюдателя до активного исследователя. , а также привитие интереса к предмету на примерах прикладных задач.

Задачи:

• Создание атмосферы заинтересованности каждого ученика в работе.

• Стимулирование учащихся к высказываниям, использованию различных способов выполнения заданий без боязни ошибиться.

• Создание обстановки для естественного самовыражения ученика.

• Создание условий для качественной отработки уровня обязательной подготовки учащихся, а также своевременное выявление и ликвидация возможных пробелов.

 Тип урока: урок проверки и коррекции знаний, умений и навыков учащихся.

Оборудование:

1. Учебник. Геометрия 7 – 9. А.В. Погорелов

2. Карточки с вопросами

3. Циркуль, карандаш, линейка

4. Таблица со справочным материалом

1. Этапы урока:

1 этап – организационный момент.

2 этап – подготовительный.

а) актуализация знаний учащихся;

б) теоретическая самостоятельная работа для контроля усвоения теоретических знаний предыдущих уроков.

в) Устный ответ теоретического материала

г) Проверка домашней задачи..

3 этап - основной. Практическая часть.

а) решение задач по готовым чертежам;

б) Решение задач из открытого банка заданий и проверка умений учащихся применять знания в изменённых условиях.

4 этап – заключительный.

5 этап-постановка домашнего задания.

I. Организационный момент.

II.Подготовительный этап.

1..Доказательство теоремы о подобных многоугольниках

2.Математический диктант

1. В любой треугольник можно вписать окружность? (Да/Нет)

2. Центр вписанной в треугольник окружности является …

3. Вокруг любого треугольника можно описать окружность? (Да/Нет)

4. Центр окружности описанной около треугольника является …

5. Если центр вписанной и описанной окружности совпадают, то это треугольник …

6. Центр окружности, описанной около прямоугольного треугольника, совпадает с …

7. Если в трапецию можно вписать окружность, то …

8. Если вокруг трапеции можно описать окружность, то …

9. Если центр окружности, описанной около треугольника находится вне его, то этот треугольник …

10. Если центр окружности, описанной около треугольника, находится внутри его, то треугольник

3.Проверка домашней задачи. Дан квадрат, докажите, что середины его сторон являются вершинами другого квадрата. Как относятся радиусы окружностей, вписанных в эти квадраты и описанных около них?

II.Практическая часть. Работа с учащимися по теме урока.

1..Решение задач по готовому чертежу.

2.Решение задач из открытого банка заданий

Че­ты­рех­уголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 70°, угол CAD равен 49°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

За­да­ние 10 № 339828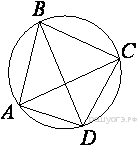

Ре­ше­ние.

Угол ABC — впи­сан­ный, опи­ра­ет­ся на дугу ADC, по­это­му ве­ли­чи­на дуги ADC равна 2 · 70° = 140°. Угол CAD — впи­сан­ный, опи­ра­ет­ся на дугу CD, по­это­му ве­ли­чи­на дуги CD равна 2 · 49° = 98°. Угол ABD — впи­сан­ный, опи­ра­ет­ся на дугу AD, по­это­му ∠ABD = ∪AD/2 = (∪ADC − ∪CD)/2 = (140° − 98°)/2 = 21°.

Ответ: 21.

46. B 6 № 316229. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABD равен 19°, угол CAD равен 35°. Най­ди­те угол ABC. Ответ дайте в гра­ду­сах.

Ре­ше­ние. угол CAD и угол CBD — впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну дугу, а зна­чит, они равны 35°. Сле­до­ва­тель­но:

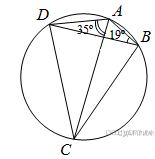
Ответ: 54

Прототип задачи №25

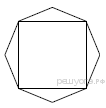Дан пра­виль­ный вось­ми­уголь­ник. До­ка­жи­те, что если его вер­ши­ны по­сле­до­ва­тель­но со­еди­нить от­рез­ка­ми через одну, то по­лу­чит­ся квад­рат.

III.Итог урока

 Устные практические задачи

1.В каком месте открытого участка треугольной формы нужно поместить фонарь, чтобы все три угла были освещены одинаково?

2. Лесная поляна имеет форму ромба. В какой точке поляны нужно находиться, чтобы одновременно услышать эхо своего возгласа от всех стен леса?

3. Считается, что громоотвод защищает от молнии все предметы, удаленные от его основания не далее его двойной высоты. Где на треугольном участке поместить громоотвод, защищающий все точки участка, чтобы высоту его сделать наименьшей?

Ответ:

 в центре окружности, описанной около треугольника. Высота громоотвода

Равна половине этого радиуса.

IV.Домашнее задание:

Повторить опорную таблицу по теме: Правильные многоугольники.

Решить задачи из банка заданий

1. 47. B 6 № 316256. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABD равен 71°, угол CAD равен 61°. Най­ди­те угол ABC. Ответ дайте в гра­ду­сах.

2. Задача 2.

В треугольнике с углам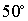и и 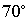 вписана окружность. Найти углы треугольника, вершинами которого являются точки касания окружности со сторонами треугольника.

Аналог задания За­да­ние 26 № 340107

3. В окруж­но­сти через се­ре­ди­ну O хорды AC про­ве­де­на хорда BD так, что дуги AB и CD равны. До­ка­жи­те, что O — се­ре­ди­на хорды BD.

За­да­ние 25 № 316360

Аналоги к заданию № 316360: 316386

Самоанализ урока геометрии в 9 классе

 Характеристика учебных возможностей учащихся

По уровню усвоения математического материала 9 класс со слабыми учебными возможностями. Из 5 учащихся 1 человек имеют 4 по предмету. Это ученик, проявляет познавательную активность, способны демонстрировать хорошие знания ранее изученного материала, свободно ими пользуются для выделения существенных признаков, обобщения, выведения новых понятий, усвоения новых знаний. У него хорошо развиты речь, логическое мышление. Постоянная потребность в повышении своего уровня развития проявляется в активном участии во внеклассных предметных мероприятиях, в поиске более сложных задач, дополнительного материала. В то же время в классе остальные дети с довольно низким уровнем обученности и слабо развитым уровнем познавательной активности. Новый материал усваивается ими только после неоднократного повторения и отработки на практике. При решении задач допускают смысловые ошибки и не всегда их находят. Речь недостаточно развита, словарный запас невелик. Самостоятельная деятельность учащихся организована с учетом их способностей и возможностей. Исходный уровень знаний, умений и навыков учащихся класса, необходимых для усвоения материала, запланированного на данный урок достаточен для достижения положительного результата.

Тема «Вписанные и описанные многоугольники» занимает важное место в курсе геометрии в связи с тем, что по логической связи курса понятие многоугольников, их свойства и признаки широко используются при изложении нового материала и решении геометрических задач в последующих разделах планиметрии и стереометрии, изучаемой в 10, 11 классах. Поэтому выработке умений и навыков применения теории, изучаемой в этой главе, следует уделить особое внимание. Изучение свойств описанных и вписанных в окружность фигур формирует пространственное представление, развивает логическое мышление и подготавливает учащихся к изучению смежных дисциплин (физика, черчение).

Урок содержит большой воспитательный потенциал, содействует формированию ответственного отношения к учению.

Данный урок приучает школьников сосредоточенно работать над решением поставленных задач, экономно расходовать время. Находясь в жёстком лимите времени, ученики должны проявить готовность и мобилизовать усилия, знания и умения на безошибочное выполнение заданий, проявить наибольшую активность в их выполнении. Задания составляются с учётом учебных возможностей учащихся.

Цели урока:

образовательная:

- Повторить и обобщить основные сведения о вписанных и описанных многоугольниках.

-Совершенствовать навыки решения задач на применение теорем о вписанных и описанных многоугольниках , вписанных и центральных углах, а формул для радиусов вписанных и описанных окружностей треугольников.

развивающая: Развивать логическое мышление,  внимание; развивать приемы мыслительной деятельности: анализ, синтез, сравнение, обобщение, классификация; развивать математическую речь

Показать применение данной темы при решении задач с практическим содержанием., формировать критическую оценку своей деятельности , а также развивать у учащихся пространственное воображение.

воспитательная :Воспитывать навыки самоконтроля, привычки к рефлексии; добиваться изменения роли ученика в учебном процессе от пассивного наблюдателя до активного исследователя. , а также. привитие интереса к предмету на примерах прикладных задач.

Задачи:

• Создание атмосферы заинтересованности каждого ученика в работе.

• Стимулирование учащихся к высказываниям, использованию различных способов выполнения заданий без боязни ошибиться.

• Создание обстановки для естественного самовыражения ученика.

• Создание условий для качественной отработки уровня обязательной подготовки учащихся, а также своевременное выявление и ликвидация возможных пробелов.

Для достижения поставленных целей использованы следующие приёмы и методы: словесные, наглядные, практические, исследовательские, проблемные (опорная таблица, задачи с готовыми чертежами, карточки для индивидуальной работы), методы устного и письменного контроля, самоконтроля, взаимоконтроля. Весь урок построен на коммуникативно -деятельностной основе.

В ходе урока проводилась работа по формированию коммуникативной компетенции (например, умению общаться устно и письменно по данной теме, грамотно отвечать на поставленные вопросы, оценивать свои и ответы своих одноклассников). Считаю, что оптимально были выбраны формы работы(фронтальная, индивидуальная, с учётом дифференциации ),рационально было распределено время на всех этапах урока. Урок был спланирован таким образом, что учащиеся на всём протяжении настраиваются на сосредоточенную и активную работу.

1. Этапы урока:

1 этап – организационный момент.

2 этап – подготовительный.

а) актуализация знаний учащихся;

б) теоретическая самостоятельная работа для контроля усвоения теоретических знаний предыдущих уроков.

в) Устный ответ теоретического материала

Г) Проверка домашней задачи..

3 этап - основной. Практическая часть.

а) решение задач по готовым чертежам;

б) Решение задач из открытого банка заданий и проверка умений учащихся применять знания в изменённых условиях.

4 этап – заключительный.

5 этап-постановка домашнего задания.

Цель организационной части — создать рабочую обстановку на уроке. 1 этап –включал в себя предварительную организацию класса, мобилизующее начало урока, мотивацию деятельности учащихся, создание психологической комфортности и подготовку учащихся к активной работе на уроке.

Основной задачей подготовительного этапа является восстановление в памяти учащихся знаний, необходимых для систематизации и обобщения изученных понятий и свойств. Выяснить уровень усвоения теоретического материала каждым учащимся.

Повторение и закрепление изученного проводилось фронтально с помощью опорной таблицы. Одновременно шла эффективная работа над развитием речи, мыслительных операций, умением корректировать свои ответы и ответы товарищей, о чем свидетельствовала деятельность учащихся.

Фронтальная работа даёт возможность включать большую часть класса в учебную деятельность. В ходе такой работы учащиеся отвечают на вопросы, дополняют и уточняют друг друга. При этом учащиеся делают общие выводы и формулировки четвертых позволяют ученикам в наиболее короткое время разобрать и уяснить учебный материал.

Также в время подготовительного этапа проводилось выяснение уровня усвоения теоретического материала каждым учащимся.

4 ученика участвовали в математическом диктанте, который был оценен на следующем уроке. В результате каждый ребенок смог себя проверить, осознать: все ли он понял, запомнил ли. Результаты: 2 ученика получили оценку «4» и 2-«3».

Цель основного этапа – активизировать осмысление знаний учащихся за счёт оперирования ими в новых ситуациях, включать учеников в репродуктивно – поисковую и частично поисковую деятельность.

Задание выполнялись письменно на доске под контролем учителя.

Заключительный этап анализ усвоения учебного материала осуществлялся с помощью наблюдения за деятельностью учащихся на уроке, на основании этого были выставлениы следующие оценки:

Т. В.- решал задачу у доски, оценка «4» , С. В. доказывал теорему о подобии правильных многоугольников оценка «4», М. Д. решала у доски задачу на доказательство оценка «4»,

Этап постановки домашнего задания организован с учётом математических способностей учащихся, закрепления знаний и умений по пройденной теме в ходе выполнения задач в классе.

Учет индивидуальных особенностей учащихся заключался в том, что учащиеся выполняют домашнее задание, соответствующее уровню их учебных возможностей, аналогичные классной работе.

• Урок цели достиг. Поставленные задачи были успешно решены. Содержание урока соответствует требованиям учебной программы по предмету.

• Все использованные на уроке методы и формы работы, а также сама организация урока сработали на достижение цели урока.

• На уроке применялась технология дифференцированного обучения. Шло обучение сразу нескольких категорий школьников: учеников, имеющих только базовый уровень знаний, учеников, умеющих выполнять задания повышенного уровня.

• В ходе работы ребята показали уровень усвоения материала, сформированность умений и навыков, были внимательны, вежливы, терпеливы по отношению друг к другу, излагали изученный материал последовательно .

• На уроке присутствовала атмосфера поиска.

Учитель математики МБОУ «Пугачевская СОШ»

________________Димитрова Л.П.

31.01.19г.