Решение задач рубрики "Наблюдайте, рисуйте, конструируйте, фантазируйте" (9 класс, Мерзляк А.Г. и др.)

Решение задач рубрики «Наблюдайте, рисуйте, конструируйте, фантазируйте»

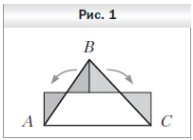
№ 877. Покажите, что любой треугольник можно разрезать на три части так, что из полученных частей можно сложить прямоугольник.

Решение: Пусть AC — наибольшая сторона треугольника ABC. Нужное разрезание показано на рисунке 1.

№ 878. В круг радиуса 1 см вписан пятиугольник. Докажите, что сумма длин его сторон и диагоналей меньше 17 см.

Доказательство: Каждая из пяти диагоналей пятиугольника не превосходит 2 см, а периметр пятиугольника меньше длины окружности, ограничивающей данный круг. Поэтому указанная сумма 10 +2 π

№ 879. Дан квадрат размером 99 х 99 клеток. Каждая клетка квадрата окрашена в чёрный или в белый цвет. Разрешается одновременно перекрасить все клетки некоторого столбца или некоторой строки в тот цвет, клеток которого в этом столбце или в этой строке до перекрашивания было больше. Всегда ли можно добиться того, чтобы все клетки квадрата стали окрашенными в один цвет?

Ответ: Да.

Решение: В данном квадрате найдутся не меньше 45 столбцов, в каждом из которых доминирует один и тот же цвет, например белый. Тогда все эти столбцы можно перекрасить в белый цвет. После этого в каждой строке найдётся по крайней мере 45 белых клеток. Все эти строки можно перекрасить в белый цвет.

№ 880. На плоскости отметили несколько точек. Некоторые из них отметили красным цветом, другие – синим. Известно, что точек каждого цвета не меньше трёх и никакие три точки одного цвета не лежат на одной прямой. Докажите, что какие-то три точки одного цвета являются вершинами треугольника, на сторонах которого может лежать не более двух точек другого цвета.

Решение: Рассмотрим все треугольники, вершины каждого из которых одного цвета. Среди этих треугольников выберем треугольник наименьшей площади. Он является искомым.

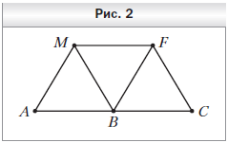
№ 881. На плоскости отметили точки А и В. С помощью одного циркуля постройте точку С такую, чтобы точка В являлась серединой отрезка АС.

Решение: Построим вершину M равностороннего треугольника AMB (рис. 2). Построим вершину F равностороннего треугольника MFB (точки A и F лежат в разных полуплоскостях относительно прямой MB). Построим вершину C равностороннего треугольника BFC (точки C и M лежат в разных полуплоскостях относительно прямой BF). Найденная таким образом точка C — искомая.

№ 882. Какое наименьшее значение может принимать радиус круга, из которого можно вырезать треугольник со сторонами 2 см, 3 см, 4 см?

Ответ: 2 см.

Решение: Радиус круга не может быть меньше, чем 2 см, так как наибольшая сторона треугольника равна 4 см. Поскольку данный треугольник тупоугольный, то вершина тупого угла принадлежит кругу, диаметром которого является наибольшая сторона.

№ 883. Можно ли из квадрата со стороной 10 см вырезать несколько кругов, сумма диаметров которых больше 5 м?

Ответ: Да.

Решение: Разобьём данный квадрат на 10 000 квадратов со стороной 1 мм. Тогда сумма диаметров всех кругов, вписанных в полученные квадраты, равна 10 м.

№ 884. Дан квадрат размером 101 х 101 клеток. Клетки квадрата раскрасили в шахматном порядке в чёрный и белый цвета так, что центральная клетка оказалась чёрной. Для каждой пары разноцветных клеток откладывают вектор, начало которого совпадает с центром чёрной клетки, а конец – с центром белой. Докажите, что сумма всех отложенных векторов равна нуль-вектору.

Доказательство: Все проведённые векторы можно разбить на пары векторов, симметричных относительно центра центральной клетки. Поэтому векторы в этих парах являются противоположными.

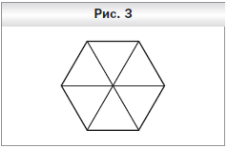
№ 885. Внутри правильного шестиугольника со стороной 1 м расположено 7 точек. Докажите, что среди них найдутся 2 точки на расстоянии не больше 1 м.

Доказательство: Разделим данный шестиугольник на шесть правильных треугольников (рис. 3). Тогда по крайней мере две из данных точек принадлежат одному из треугольников. Расстояние между этими точками не больше стороны треугольника.

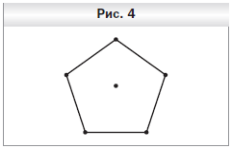
№ 886. Отметьте на плоскости 6 точек так, чтобы любые 3 из них являлись вершинами равнобедренного треугольника.

Решение: Отметим пять вершин правильного пятиугольника и его центр (рис. 4). Эти шесть отмеченных точек удовлетворяют условию задачи.