Решение задач рубрики «Наблюдайте, рисуйте, конструируйте, фантазируйте»
35. Белая плоскость произвольно забрызгана чёрной краской. Докажите, что на плоскости найдётся отрезок длиной 1 м, концы которого закрашены одним цветом.
Ответ: Рассмотрим на этой плоскости равносторонний треугольник, сторона которого равна 1 м. Тогда из трёх его вершин найдутся две вершины, окрашенные в один цвет.
8 9. Можно ли квадрат размером 10 х 10 клеток разрезать на 25 фигур, которые состоят из четырёх клеток и имеют такой вид: ?
9. Можно ли квадрат размером 10 х 10 клеток разрезать на 25 фигур, которые состоят из четырёх клеток и имеют такой вид: ?
О твет: Нельзя. Раскрасим клетки квадрата в шахматном порядке (рис. 19). Тогда квадрат будет содержать 50 белых и 50 чёрных клеток. При разрезании квадрата фигурка заданной формы содержит нечётное количество белых клеток (одну или три). Тогда 25 таких фигурок будут содержать также нечётное количество белых клеток. Получили противоречие, так как в квадрате 10 × 10, раскрашенном в шахматном порядке, количество белых клеток чётное.
твет: Нельзя. Раскрасим клетки квадрата в шахматном порядке (рис. 19). Тогда квадрат будет содержать 50 белых и 50 чёрных клеток. При разрезании квадрата фигурка заданной формы содержит нечётное количество белых клеток (одну или три). Тогда 25 таких фигурок будут содержать также нечётное количество белых клеток. Получили противоречие, так как в квадрате 10 × 10, раскрашенном в шахматном порядке, количество белых клеток чётное.
1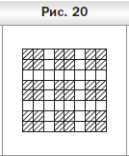 10. Учитель предложил ученику вырезать из листа картона размером 8 х 8 клеток восемь квадратов размером 2 х 2 клетки при условии не портить клетки, которые остались. Потом оказалось, что нужен ещё один такой квадрат. Всегда ли можно вырезать его из остатков листа?
10. Учитель предложил ученику вырезать из листа картона размером 8 х 8 клеток восемь квадратов размером 2 х 2 клетки при условии не портить клетки, которые остались. Потом оказалось, что нужен ещё один такой квадрат. Всегда ли можно вырезать его из остатков листа?
Ответ: Всегда можно. Раскрасим квадрат 8 × 8 так, как показано на рисунке 20. Тогда при вырезании квадратов 2 × 2 будет задето не более восьми раскрашенных квадратов. Поэтому один закрашенный квадрат гарантированно останется.
135. На плоскости отметили 1000 точек. Докажите, что существует прямая, относительно которой в каждой полуплоскости лежат по 500 точек.
Ответ: Через каждые две данные точки проведём прямую. Количество построенных прямых конечно. Следовательно, существует прямая, не параллельная ни одной из проведённых прямых. Проведём эту прямую так, чтобы данные точки лежали в одной полуплоскости относительно неё. Начнём сдвигать эту прямую параллельно самой себе в сторону отмеченных точек. При каждом положении этой прямой на ней может оказаться не более одной точки. Поэтому таким сдвигом можно добиться желаемого результата.
1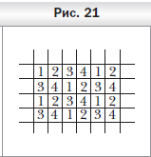 64. На бумаге в клетку выбрали произвольно 100 клеток. Докажите, что среди них можно найти не менее 25 клеток, не имеющих общих точек.
64. На бумаге в клетку выбрали произвольно 100 клеток. Докажите, что среди них можно найти не менее 25 клеток, не имеющих общих точек.
Ответ: Раскрасим лист бумаги в четыре цвета так, как показано на рисунке 21 (цвета обозначены цифрами). Тогда клетки одного цвета не имеют общих точек. Из 100 выбранных клеток найдутся, по крайней мере, 25 клеток одного цвета.
188. Расположите на плоскости восемь точек так, чтобы на серединном перпендикуляре любого отрезка с концами в этих точках лежали ровно две из этих точек.
О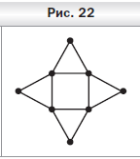 твет: На сторонах квадрата во внешнюю сторону построим равносторонние треугольники (рис. 22). Искомые точки — это вершины квадрата и вершины равносторонних треугольников, не являющиеся вершинами квадрата.
твет: На сторонах квадрата во внешнюю сторону построим равносторонние треугольники (рис. 22). Искомые точки — это вершины квадрата и вершины равносторонних треугольников, не являющиеся вершинами квадрата.
215. Пять точек принадлежат равностороннему треугольнику, сторона которого равна 1 см. докажите, что из этих точек можно выбрать две, расстояние между которыми не более 0,5 см.
О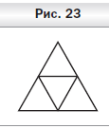 твет: Разделим равносторонний треугольник на четыре равных равносторонних треугольника, длины сторон которых равны 0,5 см (рис. 23). Тогда в один из этих треугольников попадут, по крайней мере, две из данных точек. Они и будут искомыми.
твет: Разделим равносторонний треугольник на четыре равных равносторонних треугольника, длины сторон которых равны 0,5 см (рис. 23). Тогда в один из этих треугольников попадут, по крайней мере, две из данных точек. Они и будут искомыми.
277. Многоугольник разбит диагоналями на треугольники, которые окрашены в чёрный и белый цвета так, что любые два треугольника, имеющие общую сторону, окрашены в разные цвета. Докажите, что количество чёрных треугольников не больше утроенного количества белых треугольников.
Ответ: Каждый чёрный треугольник граничит не более чем с тремя белыми треугольниками.
325. Клетки квадрата размером 100 х 100 клеток раскрашены в шахматном порядке. Квадрат разрезали на квадраты, стороны которых содержат нечётное количество клеток, и в каждом таком квадрате отметили центральную клетку. Докажите, что белых и чёрных клеток отмечено поровну.
Ответ: Для любого квадрата рассмотрим число, равное Sб − Sч, где Sб — количество белых клеток квадрата, Sч — количество чёрных клеток квадрата. Для квадрата 100 × 100 клеток Sб − Sч = 0. Для каждого квадрата, сторона которого содержит нечётное количество клеток, число Sб − Sч равно 1 (для квадрата, в котором центральная клетка белая) или −1 (для квадрата, в котором центральная клетка чёрная). Если найти сумму этих чисел для всех квадратов, на которые разрезан большой квадрат, получим 0. А это означает, что в этой сумме количество слагаемых, равных 1, и количество слагаемых, равных −1, одинаковое.
367. Можно ли квадрат разрезать на тысячеугольник и 199 пятиугольников?
Ответ: Нельзя. Каждая вершина тысячеугольника является или вершиной пятиугольника, или вершиной квадрата. Значит, общее количество вершин пятиугольников и квадрата должно быть не менее 1000. А их на самом деле
199 × 5 + 4 = 999
422. Равносторонний треугольник покрыт пятью меньшими равными между собой равносторонними треугольниками. Докажите, что для покрытия достаточно и четырёх таких треугольников.
О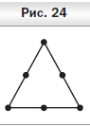 твет: Рассмотрим шесть точек, принадлежащих данному равностороннему треугольнику: три его вершины и три середины его сторон (рис. 24). Тогда, по крайней мере, одному из пяти равносторонних треугольников принадлежат две отмеченные точки. Следовательно, сторона этого треугольника не меньше половины стороны большого равностороннего треугольника. Значит, четырёх таких треугольников достаточно для покрытия.
твет: Рассмотрим шесть точек, принадлежащих данному равностороннему треугольнику: три его вершины и три середины его сторон (рис. 24). Тогда, по крайней мере, одному из пяти равносторонних треугольников принадлежат две отмеченные точки. Следовательно, сторона этого треугольника не меньше половины стороны большого равностороннего треугольника. Значит, четырёх таких треугольников достаточно для покрытия.
448. На плоскости отметили 25 точек так, что среди любых трёх из них найдутся две точки, расстояние между которыми меньше единицы. Докажите, что существует окружность единичного радиуса, которая содержит не менее 13 данных точек.
Ответ: Из данных точек выберем две, расстояние между которыми наибольшее. Проведём окружности единичного радиуса с центрами в данных точках. Каждая из оставшихся 23 точек расположена внутри одной из окружностей. Следовательно, внутри одной из окружностей содержатся, по крайней мере, 12 из 23 точек.
4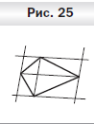 88. Как два равных выпуклых четырёхугольника разрезать на части, из которых можно составить параллелограмма?
88. Как два равных выпуклых четырёхугольника разрезать на части, из которых можно составить параллелограмма?
Ответ: Если через каждую вершину выпуклого четырёхугольника провести прямую, параллельную диагонали четырёхугольника, то точки пересечения проведённых прямых будут являться вершинами параллелограмма (рис. 25). Этот параллелограмм состоит из треугольников, на которые диагонали разрезают данные четырёхугольники.
509. На окружности отметили 999 точек синим карандашом и одну точку красным карандашом. Каких многоугольников с вершинами в отмеченных точках больше: тех, которые содержат красную точку, или тех, которые её не содержат?
Ответ: Многоугольников, содержащих красную точку, больше. Рассмотрим множество многоугольников, все вершины которых синие. Каждому такому многоугольнику соответствует, по крайней мере, один многоугольник, полученный из данного многоугольника добавлением к его вершинам красной точки. Значит, многоугольников, содержащих красную точку, не меньше, чем многоугольников, все вершины которых синие. Однако треугольник с двумя синими вершинами и одной красной не соответствует ни одному многоугольнику с синими вершинами.
528. У вписанного в окружность многоугольника выбрали вершину и провели все диагонали, которым эта вершина принадлежит. Докажите, что среди образовавшихся треугольников не более чем один является остроугольным.
Ответ: Центр окружности может лежать внутри только одного из образовавшихся треугольников. Он и будет остроугольным.
578. В квадрате со стороной 1 м произвольным образом отметили 51 точку. Докажите, что среди этих точек существует три, которые можно накрыть квадратом со стороной 20 см.
Ответ: Разобьём данный квадрат на 25 квадратов со стороной 20 см. Тогда найдётся квадрат, содержащий, по крайней мере, 3 из данных 51 точки.
6 06. Даны два круга, которые не имеют общих точек. Существует ли точка, которая не принадлежит ни одному из кругов, такая, что любая прямая, проходящая через эту точку, пересекает хотя бы один из этих кругов?
06. Даны два круга, которые не имеют общих точек. Существует ли точка, которая не принадлежит ни одному из кругов, такая, что любая прямая, проходящая через эту точку, пересекает хотя бы один из этих кругов?
Ответ: Существует. Проведём общие внешнюю и внутреннюю касательные к данным окружностям. Любая точка, лежащая внутри «криволинейного треугольника» (рис. 26), вершинами которого являются точки касания и точка пересечения касательных, удовлетворяет условию задачи.
640. Разрежьте ромб на четыре четырёхугольника так, чтобы каждый из них являлся вписанным в окружность и описанным около окружности.
О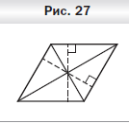 твет: Способ разрезания показан на рисунке 27 пунктирными линиями.
твет: Способ разрезания показан на рисунке 27 пунктирными линиями.
665. На окружности, радиус которой равен 1, отметили 1000 точек. Докажите, что найдётся точка, принадлежащая данной окружности, сумма расстояний от которой до отмеченных точек больше 1000.
Ответ: Обозначим точки так: M1, M2, ..., M1000. Через центр O окружности проведём диаметр AB, концам которого не принадлежит ни одна из данных точек. Известно, что сумма двух сторон треугольника больше удвоенной медианы, проведённой к третьей стороне. Тогда можно записать MiA + MiB 2MiO = 2, где i = 1, 2, ..., 1000. Тогда одна из сумм 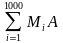 или
или 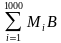 больше 1000.
больше 1000.
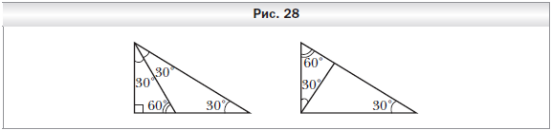
696. Каждый из двух подобных треугольников разрезали на два треугольника так, что одна из получившихся частей одного треугольника подобна одной из частей другого треугольника. Верно ли, что оставшиеся части также подобны?
Ответ: Неверно. Пример показан на рисунке 28.
720. Докажите, что в выпуклом девятиугольнике найдутся две диагонали, угол между которыми меньше 7.
Ответ: В девятиугольнике можно провести 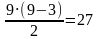 диагоналей. Выберем произвольную точку. Для каждой диагонали проведём через эту точку прямую, параллельную этой диагонали. Если какие-то две из проведённых прямых совпадут, то задача решена. Если все 27 прямых различны, то они образуют 54 угла, сумма которых равна 360°.
диагоналей. Выберем произвольную точку. Для каждой диагонали проведём через эту точку прямую, параллельную этой диагонали. Если какие-то две из проведённых прямых совпадут, то задача решена. Если все 27 прямых различны, то они образуют 54 угла, сумма которых равна 360°.
771. На плоскости даны n точек (n 3), никакие три из которых не лежат на одной прямой. Докажите, что существует треугольник с вершинами в данных точках, который не содержит ни одной из остальных (n 3) точек.
Ответ: Рассмотрим все треугольники с вершинами в данных точках. Множество таких треугольников конечно. Выберем из них треугольник наименьшей площади. Он является искомым.
805. Можно ли квадрат со стороной 1,5 см накрыть тремя квадратами со стороной 1 см?
Ответ: Нельзя. Квадрат со стороной 1 см имеет диагональ 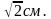 Но
Но  Следовательно, если квадрат со стороной 1 см накрывает одну вершину большого квадрата, то он не может накрыть никакую другую из трёх оставшихся вершин.
Следовательно, если квадрат со стороной 1 см накрывает одну вершину большого квадрата, то он не может накрыть никакую другую из трёх оставшихся вершин.







 9. Можно ли квадрат размером 10 х 10 клеток разрезать на 25 фигур, которые состоят из четырёх клеток и имеют такой вид: ?
9. Можно ли квадрат размером 10 х 10 клеток разрезать на 25 фигур, которые состоят из четырёх клеток и имеют такой вид: ? твет: Нельзя. Раскрасим клетки квадрата в шахматном порядке (рис. 19). Тогда квадрат будет содержать 50 белых и 50 чёрных клеток. При разрезании квадрата фигурка заданной формы содержит нечётное количество белых клеток (одну или три). Тогда 25 таких фигурок будут содержать также нечётное количество белых клеток. Получили противоречие, так как в квадрате 10 × 10, раскрашенном в шахматном порядке, количество белых клеток чётное.
твет: Нельзя. Раскрасим клетки квадрата в шахматном порядке (рис. 19). Тогда квадрат будет содержать 50 белых и 50 чёрных клеток. При разрезании квадрата фигурка заданной формы содержит нечётное количество белых клеток (одну или три). Тогда 25 таких фигурок будут содержать также нечётное количество белых клеток. Получили противоречие, так как в квадрате 10 × 10, раскрашенном в шахматном порядке, количество белых клеток чётное.  10. Учитель предложил ученику вырезать из листа картона размером 8 х 8 клеток восемь квадратов размером 2 х 2 клетки при условии не портить клетки, которые остались. Потом оказалось, что нужен ещё один такой квадрат. Всегда ли можно вырезать его из остатков листа?
10. Учитель предложил ученику вырезать из листа картона размером 8 х 8 клеток восемь квадратов размером 2 х 2 клетки при условии не портить клетки, которые остались. Потом оказалось, что нужен ещё один такой квадрат. Всегда ли можно вырезать его из остатков листа? 64. На бумаге в клетку выбрали произвольно 100 клеток. Докажите, что среди них можно найти не менее 25 клеток, не имеющих общих точек.
64. На бумаге в клетку выбрали произвольно 100 клеток. Докажите, что среди них можно найти не менее 25 клеток, не имеющих общих точек. твет: На сторонах квадрата во внешнюю сторону построим равносторонние треугольники (рис. 22). Искомые точки — это вершины квадрата и вершины равносторонних треугольников, не являющиеся вершинами квадрата.
твет: На сторонах квадрата во внешнюю сторону построим равносторонние треугольники (рис. 22). Искомые точки — это вершины квадрата и вершины равносторонних треугольников, не являющиеся вершинами квадрата.  твет: Разделим равносторонний треугольник на четыре равных равносторонних треугольника, длины сторон которых равны 0,5 см (рис. 23). Тогда в один из этих треугольников попадут, по крайней мере, две из данных точек. Они и будут искомыми.
твет: Разделим равносторонний треугольник на четыре равных равносторонних треугольника, длины сторон которых равны 0,5 см (рис. 23). Тогда в один из этих треугольников попадут, по крайней мере, две из данных точек. Они и будут искомыми.  твет: Рассмотрим шесть точек, принадлежащих данному равностороннему треугольнику: три его вершины и три середины его сторон (рис. 24). Тогда, по крайней мере, одному из пяти равносторонних треугольников принадлежат две отмеченные точки. Следовательно, сторона этого треугольника не меньше половины стороны большого равностороннего треугольника. Значит, четырёх таких треугольников достаточно для покрытия.
твет: Рассмотрим шесть точек, принадлежащих данному равностороннему треугольнику: три его вершины и три середины его сторон (рис. 24). Тогда, по крайней мере, одному из пяти равносторонних треугольников принадлежат две отмеченные точки. Следовательно, сторона этого треугольника не меньше половины стороны большого равностороннего треугольника. Значит, четырёх таких треугольников достаточно для покрытия. 88. Как два равных выпуклых четырёхугольника разрезать на части, из которых можно составить параллелограмма?
88. Как два равных выпуклых четырёхугольника разрезать на части, из которых можно составить параллелограмма? 06. Даны два круга, которые не имеют общих точек. Существует ли точка, которая не принадлежит ни одному из кругов, такая, что любая прямая, проходящая через эту точку, пересекает хотя бы один из этих кругов?
06. Даны два круга, которые не имеют общих точек. Существует ли точка, которая не принадлежит ни одному из кругов, такая, что любая прямая, проходящая через эту точку, пересекает хотя бы один из этих кругов? твет: Способ разрезания показан на рисунке 27 пунктирными линиями.
твет: Способ разрезания показан на рисунке 27 пунктирными линиями. 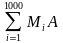 или
или 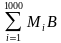 больше 1000.
больше 1000.
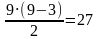 диагоналей. Выберем произвольную точку. Для каждой диагонали проведём через эту точку прямую, параллельную этой диагонали. Если какие-то две из проведённых прямых совпадут, то задача решена. Если все 27 прямых различны, то они образуют 54 угла, сумма которых равна 360°.
диагоналей. Выберем произвольную точку. Для каждой диагонали проведём через эту точку прямую, параллельную этой диагонали. Если какие-то две из проведённых прямых совпадут, то задача решена. Если все 27 прямых различны, то они образуют 54 угла, сумма которых равна 360°. 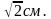 Но
Но  Следовательно, если квадрат со стороной 1 см накрывает одну вершину большого квадрата, то он не может накрыть никакую другую из трёх оставшихся вершин.
Следовательно, если квадрат со стороной 1 см накрывает одну вершину большого квадрата, то он не может накрыть никакую другую из трёх оставшихся вершин.









