Решение задач рубрики «Учимся делать нестандартные шаги»
2




 6. Даны два числа: а = 44…4 , b = 33…3 . Можно ли подобрать такие m и n, чтобы:
6. Даны два числа: а = 44…4 , b = 33…3 . Можно ли подобрать такие m и n, чтобы:
m цифр n цифр
1) число а было делителем числа b;
2) число b было делителем числа а?
Ответ: 1) нельзя; 2) можно. Решение. 1) Поскольку число b = 33…3 не имеет чётных
n цифр
делителей, то число a = 44... 4 не является делителем числа b ни при каких значениях m
m цифр
и n. 2) Запишем a =4 ⋅11...1 , b = 3⋅ 11...1 . Теперь ясно, что значение m надо искать
m цифр n цифр
среди чисел, кратных 3. Заметим, что 111 111 = 11 · 10 101. Тогда условию удовлетворяют m = 6, n = 2.
67. На сторонах квадрата записаны четыре натуральных числа. В каждой вершине квадрата записано число, равное произведению чисел, записанных на сторонах, для которых эта вершина является общей. Сумма чисел, записанных в вершинах, равна 55. Найдите сумму чисел, записанных на сторонах квадрата.
Ответ: 16.
Решение. Пусть числа, записанные на сторонах квадрата, равны a, b, c и d. Тогда в вершинах квадрата записаны числа ab, bc, cd и da. Из условия следует, что ab + bc + cd + + da = 55. Раскладывая на множители левую часть полученного равенства, получаем (a + c)(b + d) = 55. Заметим, что значение каждого из выражений (a + c) и (b + d) больше 1 и является делителем числа 55. Отсюда получаем две возможности: a + c = 5, b + d = 11 или a + c = 11, b + d = 5. В обоих случаях a + b + c + d = 16.
97. Может ли чётное число иметь нечётных делителей больше, чем чётных?
Ответ: Не может.
Решение. Каждому нечётному делителю d чётного числа можно поставить в соответствие его чётный делитель, равный 2d. Таким образом, количество чётных делителей не меньше, чем количество нечётных.
142. Два парома одновременно отплывают от противоположных берегов реки и пересекают её перпендикулярно берегам. Скорости паромов постоянные, но разные. Паромы встречаются на расстоянии 720 м от одного из берегов, после чего продолжают движение. Достигнув берегов, паромы сразу начинают двигаться обратно и через некоторое время встречаются на расстоянии 400 м от другого берега. Какова ширина реки?
Ответ: 1760 метров.
Решение. Сумма расстояний, которые паромы прошли до первой встречи, равна ширине реки, а сумма расстояний, которые они прошли к моменту второй встречи, равна утроенной ширине реки. Значит, до момента второй встречи прошло в три раза больше времени, чем до момента первой встречи. Следовательно, если к моменту первой встречи один из паромов прошёл 720 метров, то к моменту второй встречи он прошёл 2160 метров, что на 400 метров превышает ширину реки.
175. Вася и Петя по очереди заменяют в уравнении х4 + *х3 + *х2 + *х + * = 0 один знак * на некоторое число. Первым замену делает Вася. Петя хочет получить уравнение, которое имеет корень. Может ли Вася ему помешать?
Ответ: Не может.
Решение. Своим последним ходом Пете достаточно заменить оставшийся знак * таким числом, чтобы сумма коэффициентов полученного многочлена была равной нулю. В этом случае корнем многочлена является число 1.
204. На доске написаны многочлены х + 2 и 2х + 1. Разрешается записать сумму, разность или произведение любых двух из уже написанных многочленов. Может ли на доске появиться многочлен 2х3 + х + 5?
Ответ: Не может.
Решение. Заметим, что при x = 1 значения многочленов x + 2 и 2x + 1 кратны 3. Таким же свойством обладает любой многочлен, который можно получить с помощью указанных в условии операций. Остаётся заметить, что значение многочлена 2x3 + x + 5 при x = 1 равно 8.
230. Существует ли натуральное число, которое при умножении на 2 становится квадратом натурального числа, а при умножении на 3 – кубом натурального числа?
Ответ: Существует.
Решение. Существует бесконечно много чисел, удовлетворяющих условию задачи. Например, подходит любое число вида 26k + 3 · 36m + 2, где k ∈ N, m ∈ N.
273. В некотором доме живут только супружеские пары с маленькими детьми, причём у каждого мальчика есть сестра и мальчиков больше, чем девочек. Может ли взрослых быть больше, чем детей?
Ответ: Не может.
Решение. Из условия следует, что в каждой семье есть дочь. Поэтому дочерей не меньше, чем матерей. Мальчиков в доме больше, чем девочек. Это означает, что сыновей в доме больше, чем отцов. Таким образом, детей в доме больше, чем взрослых.
311. По окончании теннисного турнира, который проводился по олимпийской системе (проигравший выбывает), оказалось, что только 32 участника выиграли больше встреч, чем проиграли. Сколько теннисистов принимало участие в турнире?
Ответ: 128 теннисистов.
Решение. Выиграли больше встреч, чем проиграли, те и только те теннисисты, которые одержали не менее двух побед. По условию есть 32 таких теннисиста. Во втором туре они выиграли матчи у 32 соперников. Таким образом, в первом туре победу одержали 64 теннисиста, а участие в турнире принимали 128 теннисистов.
349. Каждый их трёх учеников написал 100 разных слов. После этого слова, которые встретились не менее двух раз, вычеркнули. В результате у одного ученика осталось 45 слов, у второго – 68, а у третьего – 78. Докажите, что по крайней мере одно слово записали все трое.
Решение. У первого ученика вычеркнуто 55 слов, у второго − 32 слова, у третьего − 22 слова. Если предположить, что каждое слово было записано не более двух раз, то общее количество слов, вычеркнутых любыми двумя учениками, не меньше количества слов, вычеркнутых третьим учеником. Поскольку 55 32 + 22, то по крайней мере одно слово было записано всеми учениками.
376. Натуральные числа x, y, z таковы, что значения выражений x + y, y + z, x + z – простые числа. Докажите, что среди чисел x, y, z есть по крайней мере два числа, равные 1.
Решение. Заметим, что сумма трёх данных простых чисел является чётным числом. Действительно, (x + y) + (y + z) + (z + x) = 2(x + y + z). Это означает, что по крайней мере одно из этих чисел чётное, а значит, равно 2. Остаётся заметить, что сумма двух натуральных чисел равна 2 лишь при условии, когда каждое из этих чисел равно 1.
421. Найдите все трёхзначные натуральные числа n такие, что сумма цифр числа n в 11 раз меньше самого числа n.
Ответ: 198.
Решение. Пусть  – искомое трёхзначное число. Тогда можно записать 100x + 10y + z = = 11(x + y + z). Отсюда 89x = y + 10z. Таким образом, значение выражения y + 10z кратно числу 89. Кроме того, поскольку x, y и z − цифры, то y + 10z y + 10z = 89, x = 1. Очевидно, что при z = 9 имеем y + 10z 89, а при z ≤ 7 имеем y + 10z z = 8, y = 9.
– искомое трёхзначное число. Тогда можно записать 100x + 10y + z = = 11(x + y + z). Отсюда 89x = y + 10z. Таким образом, значение выражения y + 10z кратно числу 89. Кроме того, поскольку x, y и z − цифры, то y + 10z y + 10z = 89, x = 1. Очевидно, что при z = 9 имеем y + 10z 89, а при z ≤ 7 имеем y + 10z z = 8, y = 9.
437. Петя и Коля ежедневно записывают по одному числу. В первый день каждый из мальчиков записал число 1. В каждый последующий день Петя записывает число 1, а Коля – число, равное сумме чисел, записанных мальчиками за предыдущие дни. Может ли в какой-то день Коля записать число, оканчивающееся на 101?
Ответ: Не может.
Решение. В первый, второй и третий дни Коля запишет числа 1, 2 и 5 соответственно. Заметим, что начиная с третьего дня все числа, записанные Колей, являются нечётными. Действительно, если в некоторый день, начиная со второго, Коля записал число x, то на следующий день он запишет число 2x + 1.
Предположим, что в некоторый день Коля записал число, заканчивающееся на 101. Тогда в предыдущий день им было записано число, заканчивающееся на 50, а такое число является чётным. Получили противоречие.
467. Попарно различные числа a, b, c удовлетворяют условию a2(b + c) = b2(c + a). Докажите, что a2(b + c) = b2(a + b).
Решение. Рассмотрим разность a2(b + c) − b2(c + a), равную нулю. Имеем:
a2b + a2c − b2c − b2a = ab(a − b) + c(a2 − b2) = (a − b)(ab + c(a + b)) = (a − b)(ab + ac + bc). Поскольку a − b ≠ 0, то ab + ac + bc = 0.
Теперь достаточно доказать, что разность a2(b + c) − c2(a + b) равна 0. Имеем:
a2(b + c) − c2(a + b) = a2b + a2c − c2a − c2b = ac(a − c) + b(a2 − c2) = (a − c)(ac + b(a + c)) = = (a − c)(ac + ab + bc) = 0.
495. В роте 100 солдат. Каждую ночь на дежурство выходят три солдата. Можно ли так организовать дежурство, чтобы через некоторое время каждый солдат побывал на дежурстве с каждым из остальных солдат ровно один раз?
Ответ: Нельзя.
Решение. Выберем одного из солдат роты. Чтобы для этого солдата организовать дежурство так, как сказано в условии, надо всех остальных солдат объединить в пары. А это невозможно, поскольку их 99.
523. На доске записаны 102 последовательных натуральных числа. Можно ли разбить их на две группы так, чтобы сумма чисел в каждой группе была простым числом (в каждой группе должно быть не менее двух чисел)?
Ответ: Нельзя.
Решение. Пусть n, n + 1, n + 2, …, n + 100, n + 101 − данные 102 последовательных натуральных чисел. Покажем, что сумма этих чисел является числом нечётным. Для этого не обязательно использовать формулу суммы n первых членов арифметической прогрессии (на этом этапе обучения она ещё не знакома учащимся). Достаточно представить сумму n + (n + 1) + (n + 2) + … + (n + 100) + (n + 101) в виде 51 нечётного слагаемого. Имеем:
n + (n + 1) + (n + 2) + … + (n + 100) + (n + 101) = (n + (n + 1)) + ((n + 2) + n + 3) + … + ((n + +100) + (n + 101)) = (2n + 1) + (2n + 5) + … + (2n + 201). Если предположить, что указанное в условии разбиение на две группы возможно, то сумма чисел в одной из групп является чётным числом, а значит, равна 2. Однако число 2 нельзя представить в виде суммы двух различных натуральных чисел. Получили противоречие.
580. Известно, что в некотором классе без двоек учатся не менее 95,5 % и не более 96,5 % учеников этого класса. Какое наименьшее количество учеников может быть в этом классе?
Ответ: 23 ученика.
Решение. Обозначим через n и m соответственно количество учеников класса и количество двоечников. Поскольку количество двоечников не превышает 4,5 %, то можно записать 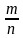 ⋅ 100 ≤
⋅ 100 ≤ 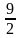 . Кроме того, известно, что количество двоечников составляет не менее 3,5 %. Это позволяет утверждать, что в классе есть по крайней мере один двоечник. А значит, m ≥ 1. Получили
. Кроме того, известно, что количество двоечников составляет не менее 3,5 %. Это позволяет утверждать, что в классе есть по крайней мере один двоечник. А значит, m ≥ 1. Получили  ≥
≥  . Отсюда n ≥
. Отсюда n ≥  . С учётом того, что n − натуральное число, получаем n ≥ 23. Остаётся заметить, что класс, состоящий из 23 учеников, из которых один двоечник, удовлетворяет условию.
. С учётом того, что n − натуральное число, получаем n ≥ 23. Остаётся заметить, что класс, состоящий из 23 учеников, из которых один двоечник, удовлетворяет условию.
615. Натуральные числа от 1 до 37 записаны в строку так, что сумма любых первых нескольких чисел делится нацело на следующее за ними число. Какое число записано на третьем месте, если на первом месте записано число 37, а на втором – 1?
Ответ: 2.
Решение. Сумма всех натуральных чисел от 1 до 37 равна 37 · 19. Ясно, что эта сумма кратна последнему из записанных чисел. Поскольку числа 37 и 1 записаны на первом и втором местах соответственно, то последнее записанное число − 19. На третьем месте записано число, которое является делителем числа 37 + 1 = 38 и не превосходит 37. Таких делителей три: 1, 2 и 19. Поскольку числа 1 и 19 записаны на втором и тридцать седьмом местах соответственно, то на третьем месте записано число 2.
655. Печатный автомат получает на входе карточку с числами (a; b) и выдаёт на выходе карточку с числами  Можно ли с помощью этого автомата из карточки с числами (0,25; 1000) получить карточку с числами (1,25; 250)?
Можно ли с помощью этого автомата из карточки с числами (0,25; 1000) получить карточку с числами (1,25; 250)?
Ответ: Нельзя.
Решение. Заметим, что  . Это означает, что произведение двух чисел, записанных на любой из полученных карточек, равно 0,25 · 1000 = 250. Поскольку 1,25 · 250 ≠ 250, то карточку (1,25; 250) получить нельзя.
. Это означает, что произведение двух чисел, записанных на любой из полученных карточек, равно 0,25 · 1000 = 250. Поскольку 1,25 · 250 ≠ 250, то карточку (1,25; 250) получить нельзя.
704. Докажите, что из 101 кубика, которые окрашены в произвольные цвета, можно выбрать или 11 кубиков одного цвета, или 11 кубиков разных цветов.
Решение. Если для окраски кубиков использовано не менее 11 цветов, то найдутся 11 кубиков разного цвета. Пусть для окраски использовали не более 10 цветов. Теперь, если предположить, что количество кубиков каждого из цветов не более 10, то общее количество кубиков не превосходит 100. Получаем противоречие.
750. Вася задумал три цифры: x, y, z. Петя называет три числа: a, b и c. Вася сообщает Пете значение выражения ax + by + cz. Какие числа должен назвать Петя, чтобы по полученной информации определить, какие цифры задумал Вася?
Ответ: a = 100, b = 10, c = 1. Решение. Если в качестве a, b и c назвать соответственно числа 100, 10 и 1, то значение выражения ax + by + cz будет равно числу  , цифры которого совпадают с теми, что задумал Вася.
, цифры которого совпадают с теми, что задумал Вася.
774. Рассматриваются все прямоугольники, длины сторон которых – натуральные числа. Каких прямоугольников больше: с периметром 1000 или с периметром 1002?
Ответ: Одинаковое количество.
Решение. Длина наименьшей стороны прямоугольника с периметром 1000 может быть любым натуральным числом от 1 до 250. Такие же значения может принимать длина наименьшей стороны прямоугольника с периметром 1002. Таким образом, между множеством прямоугольников с периметром 1000 и множеством прямоугольников с периметром 1002 можно установить взаимно однозначное соответствие.
801. На экране монитора компьютера записано число 1. Ежесекундно компьютер прибавляет к числу, находящемуся на экране, сумму его цифр. Может ли через некоторое время на экране появиться число 123 456 789?
Ответ: Не может.
Решение. Обозначим S(n) сумму цифр натурального числа n. Поскольку числа n и S(n) имеют одинаковые остатки при делении на 3, то сумма n + S(n) кратна числу 3 в том и только в том случае, когда число n кратно числу 3. Сказанное означает, что на экране монитора не может появиться число, кратное 3, а число 123 456 789 кратно 3. На самом деле на экране монитора будут чередоваться числа, дающие при делении на 3 остаток 1, и числа, дающие при делении на 3 остаток 2.
838. на тарелке лежат 9 кусочков сыра разной массы. Докажите, что можно один из кусочков сыра разрезать на две части так, что полученные 10 кусочков можно будет разложить на две тарелки и при этом масса сыра на каждой из них будет одинаковой.
Решение. Упорядочим кусочки по возрастанию массы: m1 m2 m9. На одну тарелку положим кусочки с массами m1, m3, m5, m7, а на другую − с массами m2, m4, m6, m8. Тогда m1 + m3 + m5 + m7 m2 + m4 + m6 + m8. Поскольку m3 + m5 + m7 + m9 m2 + m4 + m6 + m8, то тем более m1 + m3 + m5 + m7 + m9 m2 + m4 + m6 + m8. Тогда понятно, что m9 (m2 + m4 + +m6 + m8) − (m1 + m3 + m5 + m7). Следовательно, если обозначить d = (m2 + m4 + m6 + m8) − − (m1 + m3 + m5 + m7), то кусочек с массой, равной m9, можно разрезать на две части, удовлетворяющие условию, таким образом: 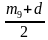 и
и 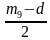 .
.








 – искомое трёхзначное число. Тогда можно записать 100x + 10y + z = = 11(x + y + z). Отсюда 89x = y + 10z. Таким образом, значение выражения y + 10z кратно числу 89. Кроме того, поскольку x, y и z − цифры, то y + 10z y + 10z = 89, x = 1. Очевидно, что при z = 9 имеем y + 10z 89, а при z ≤ 7 имеем y + 10z z = 8, y = 9.
– искомое трёхзначное число. Тогда можно записать 100x + 10y + z = = 11(x + y + z). Отсюда 89x = y + 10z. Таким образом, значение выражения y + 10z кратно числу 89. Кроме того, поскольку x, y и z − цифры, то y + 10z y + 10z = 89, x = 1. Очевидно, что при z = 9 имеем y + 10z 89, а при z ≤ 7 имеем y + 10z z = 8, y = 9. 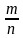 ⋅ 100 ≤
⋅ 100 ≤ 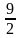 . Кроме того, известно, что количество двоечников составляет не менее 3,5 %. Это позволяет утверждать, что в классе есть по крайней мере один двоечник. А значит, m ≥ 1. Получили
. Кроме того, известно, что количество двоечников составляет не менее 3,5 %. Это позволяет утверждать, что в классе есть по крайней мере один двоечник. А значит, m ≥ 1. Получили  ≥
≥  . Отсюда n ≥
. Отсюда n ≥  . С учётом того, что n − натуральное число, получаем n ≥ 23. Остаётся заметить, что класс, состоящий из 23 учеников, из которых один двоечник, удовлетворяет условию.
. С учётом того, что n − натуральное число, получаем n ≥ 23. Остаётся заметить, что класс, состоящий из 23 учеников, из которых один двоечник, удовлетворяет условию.  Можно ли с помощью этого автомата из карточки с числами (0,25; 1000) получить карточку с числами (1,25; 250)?
Можно ли с помощью этого автомата из карточки с числами (0,25; 1000) получить карточку с числами (1,25; 250)? . Это означает, что произведение двух чисел, записанных на любой из полученных карточек, равно 0,25 · 1000 = 250. Поскольку 1,25 · 250 ≠ 250, то карточку (1,25; 250) получить нельзя.
. Это означает, что произведение двух чисел, записанных на любой из полученных карточек, равно 0,25 · 1000 = 250. Поскольку 1,25 · 250 ≠ 250, то карточку (1,25; 250) получить нельзя. 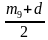 и
и 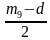 .
.
















