Решение задач рубрики «Учимся делать нестандартные шаги»
35. Все натуральные числа от 1 до 1000 включительно разбиты на две группы: чётные и нечётные. В какой из групп сумма всех цифр, используемых для записи чисел, больше и на сколько?
Ответ. Сумма цифр всех нечётных чисел на 499 больше суммы цифр всех чётных чисел. Решение. Разобьём данные числа на 500 таких пар: (2; 3), (4; 5), …, (998; 999), (1; 1000). В каждой паре, кроме последней, сумма цифр нечётного числа на 1 больше суммы цифр чётного числа.
93. Докажите, что для нечётных чисел a, b, c, d, e, f не может выполняться равенство 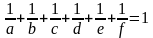 .
.
Решение. Сложим дроби, стоящие в левой части равенства. Получим дробь с нечётным знаменателем и числителем, равным сумме шести нечётных слагаемых. Отношение чётного числа к нечётному не может равняться единице.
169. Трёхзначное число n таково, что числа n − 6, n − 7 и n − 8 кратны числам 7, 8 и 9 соответственно. Найдите число n.
Ответ. 503.
Решение. Из условия следует, что число n + 1 делится нацело на 7, 8 и 9. Следовательно, оно делится на 504.
253. Натуральное число n имеет ровно 100 различных натуральных делителей (включая 1 и n). Найдите их произведение.
Ответ. n50.
Решение. Все делители данного числа можно разбить на 50 таких пар: 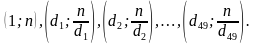 Произведение чисел в каждой паре равно n.
Произведение чисел в каждой паре равно n.
306. Для окраски одной грани кубика требуется 10 с. За какое наименьшее время 6 человек могут покрасить 101 кубик? (Два человека не могут одновременно красить один кубик.)
Ответ. 1010 с.
Решение. Если каждый человек будет красить все 6 граней кубика, то 5 последних кубиков будут красить 5 человек, и тогда работа будет выполнена за 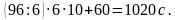 . Ясно, что наименьшее время будет затрачено в том случае, если удастся организовать работу так, что все работники будут задействованы от начала до конца. Это можно сделать, например, так. Первые 90 кубиков окрашиваются каждым человеком полностью, а затем в то время, когда 5 человек окрашивают по кубику полностью, шестой человек красит по одной грани каждого из 6 оставшихся кубиков, и, наконец, все шестеро красят по 5 граней у 6 кубиков. В этом случае на покраску будет затрачено
. Ясно, что наименьшее время будет затрачено в том случае, если удастся организовать работу так, что все работники будут задействованы от начала до конца. Это можно сделать, например, так. Первые 90 кубиков окрашиваются каждым человеком полностью, а затем в то время, когда 5 человек окрашивают по кубику полностью, шестой человек красит по одной грани каждого из 6 оставшихся кубиков, и, наконец, все шестеро красят по 5 граней у 6 кубиков. В этом случае на покраску будет затрачено 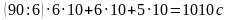 .
.
398. На доске записано число 1001. Двое играют в такую игру. За один ход нужно стереть записанное на доске число, а вместо него записать разность этого числа и любого его делителя. Ходы игроки делают поочерёдно. Проигрывает тот игрок, после хода которого на доске будет записано число 0. Кто из игроков может обеспечить себе выигрыш?
Ответ. Выигрывает второй игрок.
Решение. Если на доске написано нечётное число, то оно имеет только нечётные делители. Тогда после хода первого игрока на доске появится чётное число. Задача второго игрока состоит в том, чтобы после его хода на доске всегда оказывалось нечётное число. Для этого ему надо на своём ходе вычитать из чётного числа делитель, равный 1.
482. Существуют ли 100 таких натуральных чисел, что любая сумма нескольких из них не является квадратом натурального числа?
Ответ. Существует. Это числа 103, 105, 107, …, 10201.
Решение. Сумма любых этих чисел — это число, десятичная запись которого оканчивается на нечётное количество нулей. А такое число не является точным квадратом.
554. Каждая школа района делегировала трёх своих учеников для участия в олимпиаде. Андрей, Пётр и Елена представляли лицей «Лидер». Перед началом олимпиады всех участников выстроили в шеренгу и последовательно выдали номера участников. Андрей заметил, что после него в шеренге стоит столько же участников, сколько до него. Кроме того, Пётр и Елена оказались стоящими после Андрея и получили номера участников 19 и 28 соответственно. Сколько школ в этом районе?
Ответ. 11 школ.
Решение. Поскольку Андрей стоит в середине шеренги, то количество участников олимпиады нечётно. Номер Андрея не превосходит 18, следовательно, количество участников не больше 35. Елена имеет номер 28, следовательно, количество участников не меньше 29. Очевидно, что количество всех участников кратно трём. Таким образом, количество участников олимпиады равно 33. Тогда школ в районе 11.
605. Существуют ли такие натуральные x и y, что x4 − y4 = x3 + y3?
Ответ. Не существует.
Решение. Очевидно, что x y. Разделим обе части равенства на x + y ≠ 0. Получаем (x − y)(x2 + y2) = x2 − xy + y2. Сделаем замену:
x − y = а, а 1, xy = b, b 0. Получаем a(a2 + 2b) = a2 + b. Имеем: a3 + 2аb = a2 + b. Отсюда a2(a − 1) + b(2a − 1) = 0. В левой части последнего равенства первое слагаемое неотрицательно, а второе положительно. Поэтому это равенство противоречиво.
664. Решите уравнение 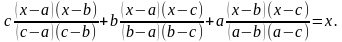
Решение. Имеем: 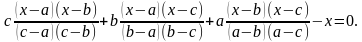 Очевидно, что a ≠ b, b ≠ c, c ≠ a. Отметим, что выражение f (x), записанное в левой части доказываемого равенства, тождественно равно или нулевому многочлену, или многочлену, степень которого не превышает 2. Предположим, что многочлен f (x) ненулевой. Легко проверить, что f (a) = f (b) = f (c) = 0. Тогда ненулевой многочлен f (x) степени не выше 2 имеет три различных корня. Следовательно, многочлен f (x) тождественно равен нулю.
Очевидно, что a ≠ b, b ≠ c, c ≠ a. Отметим, что выражение f (x), записанное в левой части доказываемого равенства, тождественно равно или нулевому многочлену, или многочлену, степень которого не превышает 2. Предположим, что многочлен f (x) ненулевой. Легко проверить, что f (a) = f (b) = f (c) = 0. Тогда ненулевой многочлен f (x) степени не выше 2 имеет три различных корня. Следовательно, многочлен f (x) тождественно равен нулю.
712. Рассматриваются квадратичные функции y = x2 + px + q, для которых p + q = 5. Докажите, что параболы, являющиеся графиками этих функций, пересекаются в одной точке.
Решение. Все эти параболы проходят через точку с координатами (1; 6).
816. Найдите все пары (х; у), удовлетворяющие уравнению 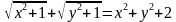 .
.
Ответ. (0; 0).
Решение. Имеем: 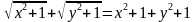 . Если а 1, то
. Если а 1, то 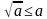 . Следовательно, левая часть данного уравнения не превосходит правой. Равенство возможно лишь при x = y = 0.
. Следовательно, левая часть данного уравнения не превосходит правой. Равенство возможно лишь при x = y = 0.
895. На плоскости расположено 100 точек. Известно, что через каждые четыре из них проходит график некоторой квадратичной функции. Докажите, что все 100 точек лежат на графике одной квадратичной функции.
Решение. Поскольку уравнение второй степени имеет не более двух корней, то графики двух квадратичных функций могут иметь не более двух общих точек. Пусть график квадратичной функции проходит через четыре из данных точек А, В, С, D и этому графику не принадлежит одна из оставшихся точек. Обозначим её D1. Тогда через точки А, В, С и D1 проходит график квадратичной функции. Получили, что два графика квадратичных функций имеют три общие точки А, В и С.
926. Глеб задумал 5 цифр: x1, x2, x3, x4, x5. Игорь отгадывает их. Ему разрешено задавать вопросы вида: «Чему равна сумма a1x1 + a2x2 + a3x3 + a4x4 + a5x5?», где a1, a2, a3, a4, a5 — некоторые натуральные числа. За какое наименьшее число вопросов Игорь может отгадать задуманные Глебом цифры?
Ответ. За один вопрос.
Решение. В качестве чисел a1, a2, a3, a4, a5 Игорь должен выбрать соответственно следующие числа: 104, 103, 102, 101, 100.







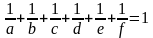 .
. 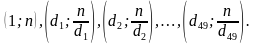 Произведение чисел в каждой паре равно n.
Произведение чисел в каждой паре равно n. 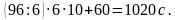 . Ясно, что наименьшее время будет затрачено в том случае, если удастся организовать работу так, что все работники будут задействованы от начала до конца. Это можно сделать, например, так. Первые 90 кубиков окрашиваются каждым человеком полностью, а затем в то время, когда 5 человек окрашивают по кубику полностью, шестой человек красит по одной грани каждого из 6 оставшихся кубиков, и, наконец, все шестеро красят по 5 граней у 6 кубиков. В этом случае на покраску будет затрачено
. Ясно, что наименьшее время будет затрачено в том случае, если удастся организовать работу так, что все работники будут задействованы от начала до конца. Это можно сделать, например, так. Первые 90 кубиков окрашиваются каждым человеком полностью, а затем в то время, когда 5 человек окрашивают по кубику полностью, шестой человек красит по одной грани каждого из 6 оставшихся кубиков, и, наконец, все шестеро красят по 5 граней у 6 кубиков. В этом случае на покраску будет затрачено 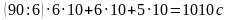 .
. 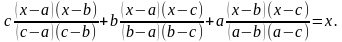
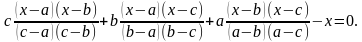 Очевидно, что a ≠ b, b ≠ c, c ≠ a. Отметим, что выражение f (x), записанное в левой части доказываемого равенства, тождественно равно или нулевому многочлену, или многочлену, степень которого не превышает 2. Предположим, что многочлен f (x) ненулевой. Легко проверить, что f (a) = f (b) = f (c) = 0. Тогда ненулевой многочлен f (x) степени не выше 2 имеет три различных корня. Следовательно, многочлен f (x) тождественно равен нулю.
Очевидно, что a ≠ b, b ≠ c, c ≠ a. Отметим, что выражение f (x), записанное в левой части доказываемого равенства, тождественно равно или нулевому многочлену, или многочлену, степень которого не превышает 2. Предположим, что многочлен f (x) ненулевой. Легко проверить, что f (a) = f (b) = f (c) = 0. Тогда ненулевой многочлен f (x) степени не выше 2 имеет три различных корня. Следовательно, многочлен f (x) тождественно равен нулю. 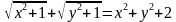 .
. 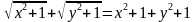 . Если а 1, то
. Если а 1, то 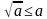 . Следовательно, левая часть данного уравнения не превосходит правой. Равенство возможно лишь при x = y = 0.
. Следовательно, левая часть данного уравнения не превосходит правой. Равенство возможно лишь при x = y = 0. 









