Решение задач рубрики «Учимся делать нестандартные шаги»
32. Дано 12 натуральных чисел. Докажите, что из них всегда можно выбрать два, разность которых делится нацело на 11.
Доказательство: Поскольку существует 11 остатков при делении на 11 (они образуют множество {0, 1, 2, ..., 10}), то по принципу Дирихле среди 12 натуральных чисел найдутся два, имеющие одинаковые остатки при делении на 11. Разность этих чисел делится нацело на 11.
78. Сколько существует шестизначных чисел, в записи которых есть хотя бы одна чётная цифра?
Ответ: 9 ⋅ 105 − 56. Количество всех шестизначных чисел равно 9 ⋅ 105. Количество всех шестизначных чисел, в записи которых все цифры нечётные, равно 56. Следовательно, искомое число равно 9 ⋅ 105 − 56.
131. Найдите все натуральные значения n, при которых значение каждого из выражений n – 2, n + 24, n + 26 является простым числом.
Ответ: 5. Рассмотрим попарные разности данных выражений.
Имеем:
(n + 26) − (n − 2) = 28;
(n + 26) − (n + 24) = 22;
(n + 24) − (n − 2) = 26.
Среди полученных разностей нет числа, кратного 3. Это означает, что при любом натуральном n значения данных выражений имеют разные остатки при делении на 3. Таким образом, одно из указанных значений кратно 3. Тогда значения выражений n − 2, n + 24, n + 26 могут быть простыми числами, если одно из них равно 3. Ясно, что возможен лишь случай, когда n − 2 = 3. Отсюда n = 5. Проверка показывает, что при n = 5 значения выражений n + 24 и n + 26 — простые числа.
151. На доске написаны числа 1, 2, 3, …, 10. За один шаг разрешается, выбрав два числа, к каждому из них прибавить 5 или из каждого вычесть 1. Можно ли с помощью этих операций добиться того, чтобы все числа, записанные на доске, оказались равными?
Ответ: нельзя. Сумма записанных на доске чисел равна 1 + 2 + 3 + ... + + 10 = 55 – число нечётное. Теперь следует заметить, что после каждой операции сумма записанных на доске чисел увеличивается на 10 или уменьшается на 2. И в том и в другом случае вновь полученная сумма чисел имеет ту же чётность, что и сумма чисел, записанных до выполнения операции. Таким образом, в любой момент сумма чисел, записанных на доске, – число нечётное. Если предположить, что в некоторый момент все 10 записанных на доске чисел оказались равными, то их сумма будет числом чётным. Получаем противоречие.
203. В некотором городе с любой станции метро можно проехать на любую другую станцию (возможно, с пересадками). Докажите, что существует станция, которую можно закрыть (без права проезда через неё), и при этом с любой из оставшихся станций можно будет проехать на любую другую.
Доказательство: Рассмотрим произвольную станцию A и наиболее удалённую от неё (по количеству остановок) станцию B. Тогда маршрут максимальной длины, начинающийся в станции A, закончится на станции B, и дальше пассажир не поедет. Значит, в случае закрытия станции B связь между станцией A и любой другой станцией сохранится. При этом связь между любыми другими станциями C и D также сохранится, потому что между ними можно проехать по маршруту C — A — D.
260. Трамвайные билеты имеют номера от 000000 до 999999. Номер называют «счастливым», если сумма трёх его первых цифр равна сумме трёх последних. Докажите, что количество «счастливых» билетов чётно.
Доказательство: Заметим, что если билет с номером abcdef «счастливый», то билет с номером 999999 − abcdef тоже «счастливый». Таким образом, все «счастливые» билеты можно разбить на пары. Также следует заметить, что номера билетов в паре совпадать не могут, поскольку их соответствующие цифры имеют разную чётность.
291. Сколькими способами можно поставить на шахматную доску белую и чёрную ладьи так, чтобы они не били друг друга?
Ответ: 64 ⋅ 49. Для белой ладьи можно выбрать любую из 64 клеток доски. После каждого такого выбора остаётся 7 ⋅ 7 = 49 клеток, которые может занять чёрная ладья. Таким образом, искомое количество способов равно 64 ⋅ 49.
305. Вокруг звезды вращается несколько планет, расстояния между которыми не изменяются и являются попарно разными. На каждой планете находится астроном, который изучает ближайшую планету. Докажите, что существуют две планеты, на которых астрономы изучают друг друга.
Решение: Поскольку все расстояния между планетами попарно различны и количество этих расстояний конечно, то найдутся две планеты, расстояние между которыми меньше, чем расстояние между любыми двумя другими. Астрономы, находящиеся на этих планетах, наблюдают друг друга.
354. Саша и Вася записывают 30-значное число, используя только цифры 1; 2; 3; 4; 5. Первую цифру пишет Саша, вторую – Вася и т.д. Вася хочет получить число, кратное 9. Сможет ли Саша ему помешать?
Ответ: Не сможет. Вася может придерживаться следующей стратегии: если Саша при своём ходе записывает некоторую цифру a, то Вася записывает цифру 6 − a. Тогда сумма цифр полученного 30-значного числа будет равной 15 ⋅ 6 = 90, а следовательно, это число будет кратно 9.
391. В волейбольном турнире, проходившем в один круг (то есть каждая команда сыграла с каждой один раз), 20 % всех команд не выиграли ни одной игры. Сколько команд участвовало в этом турнире? (Примечание. В волейболе «ничьих» не бывает, обязательно одна команда выигрывает, а другая проигрывает.)
Ответ: 5 команд. Существует не более одной команды, проигравшей все матчи. Если одна команда составляет 20 % количества всех команд, то в турнире участвовало 5 команд.
4 32. В каждой клетке доски размером 5 х 5 клеток сидит жук. В некоторый момент все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?
32. В каждой клетке доски размером 5 х 5 клеток сидит жук. В некоторый момент все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?
Ответ: Обязательно. Раскрасим доску в два цвета так, как показано на рисунке 3. Заметим, что каждый жук переползает в клетку другого цвета, чем та, в которой он находился первоначально. Тогда 12 жуков, находящихся в белых клетках, не смогут занять 13 чёрных клеток. Таким образом, после переползания жуков по крайней мере одна чёрная клетка окажется пустой.
475. Из листа картона вырезали несколько равных равносторонних треугольников. В вершинах каждого написали цифры 1, 2, 3. Потом эти треугольники сложили в стопку. Может ли получиться так, что сумма чисел вдоль каждого ребра стопки будет равна 55?
Ответ: Не может. Если предположить, что сумма чисел, записанных вдоль каждого ребра стопки, равна 55, то сумма всех записанных чисел равна 55 ⋅ 3 = 165 – число нечётное. При этом сумма чисел, записанных в вершинах каждого треугольника, равна 6. Тогда сумма всех записанных чисел равна 6n, где n – количество треугольников. Поскольку 6n – число чётное, то получаем противоречие.
498. В турнире, организованном по олимпийской системе (проигравший выбывает), участвовали n теннисистов. Какое количество матчей надо провести, чтобы определить победителя турнира?
Ответ: n − 1. В каждом матче выбывает один участник. Для того чтобы выбыл n − 1 участник, следует провести n − 1 матч.
532. Для перевозки груза выделили 4-, 7- и 8-тонные грузовики. Каждый автомобиль должен сделать только одну ходку. Сколько требуется грузовиков каждого вида для перевозки 44 т груза?
Ответ: 2 четырёхтонных грузовика, 4 семитонных, 1 восьмитонный. Обозначим количества четырёхтонных, семитонных и восьмитонных грузовиков соответственно x, y, z. Получаем 4x + 7y + 8z = 44. Отсюда 7y = 4(11 − x − 2z). Из последнего уравнения следует, что y – натуральное число, кратное 4. Кроме того, 7y y Таким образом, y = 4. Подставляя найденное значение y в исходное уравнение, получим
7x + 28 + 8z = 44. Отсюда x + 2z = 4. Теперь ясно, что x – чётное число, меньшее 4. Тогда x = 2, z = 1.
566. Меню состоит из 101 блюда. Докажите, что количество способов выбора обеда из нечётного количества блюд равно количеству способов выбора обеда из чётного количества блюд при условии, что заказать все блюда из меню нельзя.
Доказательство: Выбирая обед из n блюд, мы тем самым выбираем и обед, состоящий из оставшихся 101 − n блюд. Поскольку числа n и 101 − n имеют разную чётность, то все возможные выборы можно разбить на пары вида (n; 101 − n).
623. Известно, что натуральные числа m и n 10m + n делится нацело на 11. Докажите, что значение выражения (10m + n)(10n + m) делится нацело на 121.
Доказательство: Поскольку значение выражения 10m + n кратно 11 по условию, то достаточно доказать, что значение выражения 10n + m также кратно 11. Этот факт следует из того, что значение выражения (10m + n) + (10n + m) кратно 11. Действительно,
(10m + n) + (10n + m) = 11(m + n).
674. Можно ли натуральные числа от 1 до 32 разбить на три группы так, чтобы произведения чисел каждой группы были равны?
Ответ: Нельзя. Если предположить, что указанное разбиение возможно, то значение выражения 1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ 31 ⋅ 32 = 32! – куб натурального числа. Тогда степень каждого простого множителя, входящего в каноническое разложение числа 32!, кратна 3. Однако это не так. Например, простой множитель 31 входит в это разложение в первой степени.
706. Есть 100 кучек по 100 монет. Одна из кучек состоит из фальшивых монет, каждая из которых на 1 г легче настоящей. Масса настоящей монеты составляет 10 г. Какое наименьшее количество взвешиваний на пружинных весах со стрелкой надо сделать, чтобы найти кучку из фальшивых монет?
Ответ: Одно. Пронумеруем кучки монет натуральными числами от 1 до 100. Возьмём из каждой кучки количество монет, равное номеру этой кучки. Если кучка с фальшивыми монетами имеет номер n, то масса всех выбранных монет равна (1 + 2 + ... + 100) − n.
752. Пусть x1, x2, ..., x25 – некоторый набор натуральных чисел, а набор y1, y2, ..., y25 получен из него в результате перестановки некоторых чисел. Докажите, что значение выражения (x1 − y1) (x2 − y2)...(x25 − y25) является чётным числом.
Доказательство: В наборе x1, x2, ..., x25 найдутся либо 13 чётных чисел, либо 13 нечётных чисел. Таким же свойством обладает набор y1, y2, ..., y25. Это означает, что компоненты по крайней мере в одной из пар (x1; y1), (x2; y2), ..., (x25; y25) имеют одинаковую чётность, а из этого следует, что данное произведение — число чётное.
788. Натуральные числа х и у таковы, что 34х = 43у. Докажите, что число х + у составное.
Доказательство Имеем: 43х + 43у = 77х. Отсюда 43(х + у) = 77х. Поскольку число 43 простое, то число х + у делится нацело и на 7, и на 11. Следовательно, число х + у – составное.
820. Докажите, что в любом 60-значном числе, десятичная запись которого не содержит нулей, можно зачеркнуть несколько цифр так, что полученное в результате этого число будет делиться нацело на 1001.
Доказательство: Любое натуральное число, записанное шестью одинаковыми цифрами, делится нацело на 1 001. Остаётся заметить, что по принципу Дирихле в записи любого 60-значного числа найдутся шесть одинаковых цифр. Отметим, что условие задачи избыточно. Можно утверждать, что указанным свойством обладает любое 46-значное число, запись которого не содержит нулей.
848. Из квадратного листа бумаги в клетку, содержащего целое количество клеток, вырезали по линиям квадрат, содержащий целое количество клеток, так, что осталась 71 клетка. Сколько клеток содержал исходный лист бумаги?
Ответ: 1 296. Обозначим через m и n длины сторон листа бумаги и вырезанного квадрата соответственно. Тогда можно записать m2 − n2 = 71. Таким образом, значения выражений (m − n) и (m + n) — натуральные делители числа 71. Поскольку 0 m − n m + n и 71 – простое число, то существует единственная возможность: m − n = 1, m + n = 71. Складывая полученные равенства, получаем: 2m = 72; m = 36.
908. Есть два печатных автомата. Первый по карточке с числами (a; b; c) выдаёт карточку с числами  а второй по карточке с числами (a; b; c) – карточку с числами
а второй по карточке с числами (a; b; c) – карточку с числами  Можно ли с помощью этих автоматов из карточки (2,8; −1,7; 16) получить карточку (1,73; 2; 0,4)?
Можно ли с помощью этих автоматов из карточки (2,8; −1,7; 16) получить карточку (1,73; 2; 0,4)?
Ответ: Нельзя. Заметим, что после любой из двух описанных операций сумма чисел, записанных на карточке, не изменится. Действительно,  = a + b + c;
= a + b + c;
(2a − b) + (2b − c) + (2c − a) = a + b + c. Поскольку 2,8 + (−1,7) + 16 ≠ 1,73 + 2 + 0,4, то из карточки (2,8; −1,7; 16) получить карточку (1,73; 2; 0,4) нельзя.
949. Сравните значения выражений 
Ответ: (1 ⋅ 2 ⋅ 3 ⋅ ... ⋅ 999 ⋅ 1 000)2 1 0001 000.
Запишем очевидные неравенства:
1 ⋅ 1 000 ≥ 1 000;
2 ⋅ 999 1 000;
3 ⋅ 998 1 000;
...
998 ⋅ 3 1 000;
999 ⋅ 2 1 000;
1 000 ⋅ 1 ≥ 1 000.
Умножив почленно левые и правые части, получим (1 ⋅ 2 ⋅ 3 ⋅...⋅ 999 ⋅ 1 000)2 1 0001 000.
1006. Сумма 100 разных натуральных чисел равна 5051. Найдите эти числа.
Ответ: 1, 2, 3, ..., 99, 101. Наименьшая сумма, которая состоит из ста разных натуральных слагаемых, равна 1 + 2 + 3 + ... + 99 + 100 = 5 050. Увеличение на 1 в левой части суммы любого слагаемого, отличного от 100, влечёт необходимость увеличить по крайней мере ещё одно из слагаемых (в противном случае в сумме найдутся равные слагаемые). В таком случае сумма будет не меньше 5 052. Таким образом, существует единственный набор, удовлетворяющий условию: 1, 2, 3, ..., 98, 99, 101.
1033. Десятичная запись одного пятизначного числа состоит только из цифр 2 и 3, а другого пятизначного числа – только из цифр 3 и 4. Может ли запись произведения этих чисел состоять только из цифр 2 и 4?
Ответ: Не может. Наименьшее число, которое может быть получено в результате умножения двух чисел указанного вида, равно 22 222 ⋅ 33 333 = 740 725 926, а наибольшее – 33 333 ⋅ 44 444 = 1 481 451 852. Остаётся заметить, что в натуральном ряде между числами 740 725 926 и 1 481 451 852 нет ни одного числа, запись которого состоит из цифр 2 и 4.
1046. Найдите все целые числа x и y, при которых выполняется равенство x + y = xy .
Ответ: x = 0, y = 0 или x = 2, y = 2. Преобразуем данное уравнение. Имеем: x (y − 1) − y = 0; x (y − 1) − (y − 1) = 1; (x − 1)( y − 1) = 1. Теперь ясно, что значения выражений (x − 1) и
(y − 1) – делители числа 1.
Таким образом, существуют две возможности: 1) 
В первом случае получаем x = 2, y = 2, во втором – x = 0, y = 0.
1077. Клетки таблицы размером 101 х 101 заполнены числами так, что произведение чисел в каждом столбце является отрицательным. Может ли оказаться, что количество строк, произведение чисел в которых положительно, равно 51?
Ответ: Не может. Поскольку произведение чисел в каждом из 101 столбцов – число отрицательное, то отрицательным является произведение всех чисел таблицы (как произведение нечётного количества отрицательных множителей). Если предположить, что произведение чисел в каждой из 51 строки – положительное число, а в каждой из оставшихся 50 строк – отрицательное, то получим, что произведение всех чисел таблицы – число положительное. Таким образом, приходим к противоречию.
1138. Докажите, что квадрат натурального числа имеет нечётное количество делителей.
Доказательство: Очевидно, что число 1 указанным свойством обладает. Пусть d – делитель числа n2 (n ∈ N, n ≠ 1), отличный от n. Тогда число  – также делитель числа n2, отличный от n. Таким образом, все делители числа n2, отличные от n, можно объединить в пары вида
– также делитель числа n2, отличный от n. Таким образом, все делители числа n2, отличные от n, можно объединить в пары вида 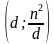 , где компоненты в каждой паре – неравные числа.
, где компоненты в каждой паре – неравные числа.







 32. В каждой клетке доски размером 5 х 5 клеток сидит жук. В некоторый момент все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка?
32. В каждой клетке доски размером 5 х 5 клеток сидит жук. В некоторый момент все жуки переползают на соседние (по горизонтали или вертикали) клетки. Обязательно ли при этом останется пустая клетка? а второй по карточке с числами (a; b; c) – карточку с числами
а второй по карточке с числами (a; b; c) – карточку с числами  Можно ли с помощью этих автоматов из карточки (2,8; −1,7; 16) получить карточку (1,73; 2; 0,4)?
Можно ли с помощью этих автоматов из карточки (2,8; −1,7; 16) получить карточку (1,73; 2; 0,4)? = a + b + c;
= a + b + c; 

 – также делитель числа n2, отличный от n. Таким образом, все делители числа n2, отличные от n, можно объединить в пары вида
– также делитель числа n2, отличный от n. Таким образом, все делители числа n2, отличные от n, можно объединить в пары вида 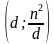 , где компоненты в каждой паре – неравные числа.
, где компоненты в каждой паре – неравные числа.









