Тип 1 № 179
Вычислите: (53 − 27 – 14) : (41 − 29).
2. Тип 2 № 236
Вычислите:
Ответ:
3. Тип 3 № 475
Доярка перелила 18 л молока из ведра в два бидона. В первом бидоне оказалось всего молока. Сколько литров молока во втором бидоне?
4. Тип 4 № 476
Вычислите: 2,1 ⋅ 2,7 + 6,43.
5. Тип 5 № 345

На рисунке изображены гитара и скрипка. Длина скрипки составляет 55 см. Определите примерную длину гитары в метрах (с точностью до десятых). Считайте, что фотографии выполнены с одинакового расстояния при одном и том же увеличении.
6. Тип 6 № 155
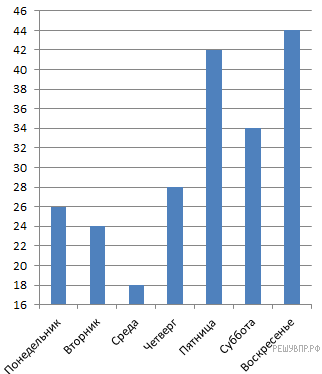 На диаграмме представлены данные о количестве посетителей литературного клуба за неделю. По вертикали указано количество посетителей. Назовите среднее количество посетителей за один день в выходные дни.
На диаграмме представлены данные о количестве посетителей литературного клуба за неделю. По вертикали указано количество посетителей. Назовите среднее количество посетителей за один день в выходные дни.
7. Тип 7 № 266
Найдите отрицательное решение уравнения
8. Тип 8 № 135
На координатной прямой отмечены точки A, B и C.
Установите соответствие между точками и их координатами.
| ТОЧКИ | КООРДИНАТЫ |
| A | 1) |
| B | 2) |
| C | 3) |
|
| 4) |
|
| 5) |
В таблице под каждой буквой укажите номер соответствующей координаты без пробелов, запятых или других дополнительных символов.
Ответ:
9. Тип 9 № 56
Вычислите: Запишите решение и ответ.
10. Тип 10 № 293
Вера складывает фигурки из бумаги. Всего у нее получилось 66 фигурок, из которых 27 лошадей, а остальные — голуби.
Выберите верные утверждения и запишите в ответе их номера без пробелов, запятых или других дополнительных символов.
1) Вера сложила одинаковое количество лошадей и голубей.
2) Вера сложила не менее 40 голубей.
3) Вера преимущественно складывала бумажных голубей.
4) У Веры получилось голубей на 12 больше, чем лошадей.
11. Тип 11 № 375
Николай в апреле весил 100 кг. В мае он сбросил 10 кг., а в июне он стал весить еще на 30% меньше, по сравнению с маем. Определите, сколько процентов от апрельского веса составляет вес Николая в июне.
12. Тип 12 № 110
На рис. 1 изображены два круга. Они разбивают плоскость на четыре части. На свободном поле справа, обозначенном как рис. 2, нарисуйте два круга так, чтобы они разбивали плоскость на три части.

13. Тип 13 № 396
Доказать, что из любых трёх целых чисел можно найти два, сумма которых чётна.









 На диаграмме представлены данные о количестве посетителей литературного клуба за неделю. По вертикали указано количество посетителей. Назовите среднее количество посетителей за один день в выходные дни.
На диаграмме представлены данные о количестве посетителей литературного клуба за неделю. По вертикали указано количество посетителей. Назовите среднее количество посетителей за один день в выходные дни.





















