Тип 1 № 170
Вычислите: 37 – 29 + 159 − 86.
2. Тип 2 № 233
Вычислите:
Ответ:


3. Тип 3 № 313
В книге 320 страниц. Петя прочитал книги. Сколько ему страниц осталось прочитать?
4. Тип 4 № 35
Вычислите:
5. Тип 5 № 347

На рисунке изображена картина в рамке. Длина картины вместе с рамкой составляет 90 см, а ширина вместе с рамкой 40 см. Определите примерную площадь полотна без рамки в квардратных метрах (с точностью до десятых).
6. Тип 6 № 144
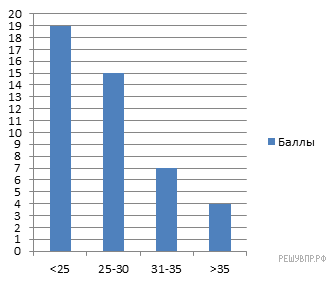 На диаграмме показаны баллы, которые набрали участники олимпиады по начертательной геометрии. По вертикальной оси указано число участников. Сколько человек принимало участие в олимпиаде?
На диаграмме показаны баллы, которые набрали участники олимпиады по начертательной геометрии. По вертикальной оси указано число участников. Сколько человек принимало участие в олимпиаде?
7. Тип 7 № 245
Найдите значение выражения при
8. Тип 8 № 133
На координатной прямой отмечены точки A, B и C.
Установите соответствие между точками и их координатами.
| ТОЧКИ | КООРДИНАТЫ |
| A | 1) |
| B | 2) |
| C | 3) |
|
| 4) |
|
| 5) |
В таблице под каждой буквой укажите номер соответствующей координаты без пробелов, запятых или других дополнительных символов.
Ответ:
9. Тип 9 № 66
Вычислите: Запишите решение и ответ.
10. Тип 10 № 272
В рыбном прилавке на витрине лежат подряд 4 карпа, 3 окуня, 2 лосося и 5 селедок.
Выберите верные утверждения и запишите в ответе их номера без пробелов, запятых или других дополнительных символов.
1) Лососей ровно в 2 раза меньше, чем селедок.
2) Карпы лежат между окунями и селедкой.
3) Больше всего в прилавке продается селедки.
4) Придя в магазин, покупатель сможет приобрести 2 набора, состоящих из 2 карпов и 1 лосося
11. Тип 11 № 360
На конец воскресенья в магазине было 220 шкафов. В понедельник было продано 40 шкафов. Определите, сколько стало шкафов в магазине, если во вторник их количество пополнилось в размере 40% от оставшихся после продажи в понедельник 40 шкафов.
12. Тип 12 № 117
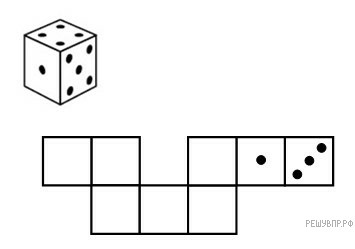
Игральный кубик прокатили по столу. На рисунке изображён след кубика. Отметьте на рисунке место, в котором грань с шестью точками соприкасалась со столом. Считайте, что сумма чисел на противоположных сторонах кубика равна 7.
13. Тип 13 № 398
Даны шесть чисел: 1, 2, 3, 4, 5, 6. Разрешается к любым двум из них прибавлять 1. Можно ли все числа сделать равными?










 На диаграмме показаны баллы, которые набрали участники олимпиады по начертательной геометрии. По вертикальной оси указано число участников. Сколько человек принимало участие в олимпиаде?
На диаграмме показаны баллы, которые набрали участники олимпиады по начертательной геометрии. По вертикальной оси указано число участников. Сколько человек принимало участие в олимпиаде?





















