Россия, Муравленко
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 07.09.2025 18:17
Кодинцева Анжелика Александровна
учитель математики
440
106 999 
Местоположение
Специализация
Результаты ОГЭ по математике
Категория:
Математика
02.03.2023 19:21
Просмотр содержимого документа
«Результаты ОГЭ по математике»
Аналитическая справка
по результатам основного государственного экзамена по математике
учащихся 9–ых классов г.Муравленко
(2020-2021 учебный год)
Характеристика структуры и содержания КИМ, особенности
Назначение контрольных измерительных материалов (КИМ) — основной государственный экзамен (ОГЭ) представляет собой форму государственной итоговой аттестации, проводимой в целях определения соответствия результатов освоения обучающимися основных образовательных программ основного общего образования требованиям федерального государственного образовательного стандарта. Для указанных целей используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы. ОГЭ проводится в соответствии с Федеральным законом от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации» и Порядком проведения государственной итоговой аттестации по образовательным программам основного общего образования, утверждённым приказом Минпросвещения России и Рособрнадзора от 07.11.2018 № 189/1513.
Документы, определяющие содержание экзаменационной работы:
содержание КИМ определяется на основе федерального государственного образовательного стандарта основного общего образования (приказ Минобрнауки России от 17.12.2010 № 1897) с учётом Примерной основной образовательной программы основного общего образования (одобрена решением Федерального учебно-методического объединения по общему образованию (протокол от 8.04.2015 № 1/15)).
В КИМ обеспечена преемственность проверяемого содержания с федеральным компонентом государственного образовательного стандарта основного общего образования по математике (приказ Минобразования
России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования»).
Структура экзаменационной работы в 9 – х классах:
Структура КИМ ОГЭ отвечает цели построения системы дифференцированного обучения математике в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования, и
одновременного создания условий, способствующих получению частью обучающихся подготовки повышенного уровня, достаточной для активного использования математики во время дальнейшего обучения.
КИМ разработаны с учётом положения о том, что результатом освоения основной образовательной программы основного общего образования должна стать математическая компетентность выпускников, т.е. они должны: овладеть специфическими для математики знаниями и видами деятельности; научиться преобразованию знания и его применению в учебных и внеучебных ситуациях; сформировать качества, присущие математическому мышлению, а также овладеть математической терминологией, ключевыми понятиями, методами и приёмами.
В экзаменационной модели используется система оценивания заданий с развёрнутым ответом, основанная на следующих принципах.
1. Возможны различные способы и записи развёрнутого решения.
Главное требование – решение должно быть математически грамотным из него должен быть понятен ход рассуждений экзаменуемого. В остальном (метод, форма записи) решение может быть произвольным. Полнота и обоснованность рассуждений оцениваются независимо от выбранного метода
решения. При этом оценивается продвижение выпускника в решении задачи, а не недочёты по сравнению с «эталонным» решением.
2. При решении задачи можно использовать без доказательств и ссылок математические факты, содержащиеся в учебниках и учебных пособиях, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования. Тексты заданий предлагаемой модели экзаменационной работы в целом соответствуют формулировкам, принятым в учебниках и учебных пособиях, включённым в Федеральный перечень учебников, рекомендуемых Министерством просвещения РФ к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего образования.
Работа содержит 25 заданий и состоит из двух частей. Часть 1 содержит 19 заданий с кратким ответом; часть 2 – 6 заданий с развёрнутым ответом.
При проверке базовой математической компетентности экзаменуемые должны продемонстрировать владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их
свойств, приёмов решения задач и проч.), умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять
математические знания в простейших практических ситуациях.
Задания части 2 направлены на проверку владения материалом на повышенном и высоком уровнях. Их назначение – дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее
подготовленных обучающихся, составляющих потенциальный контингент профильных классов. Эта часть содержит задания повышенного и высокого уровней сложности из различных разделов математики. Все задания требуют записи решений и ответа. Задания расположены по нарастанию трудности: от относительно простых до сложных, предполагающих свободное владение материалом и высокий уровень математической культуры.
Распределение заданий по частям экзаменационной работы:
| № | Часть работы | Тип заданий | Количество заданий | Максимальный первичный балл |
| 1 | Часть 1 | С кратким ответом в виде одной цифры, которая соответствует номеру правильного ответа | 2 | 2 |
| 2 | Часть 1 | С кратким ответом в виде числа, последовательности цифр | 17 | 17 |
| 3 | Часть 2 | С развернутым ответом | 6 | 12 |
|
|
|
| 25 | 31 |
Распределение заданий КИМ ОГЭ по содержанию, проверяемым умениям и способам деятельности
Часть 1. В этой части экзаменационной работы содержатся задания по всем ключевым разделам математики, отражённым в кодификаторе элементов содержания (КЭС).
Часть 2. Задания части 2 направлены на проверку таких качеств математической подготовки выпускников, как:
уверенное владение формально-оперативным алгебраическим аппаратом;
умение решить комплексную задачу, включающую в себя знания из разных тем курса алгебры;
умение решить планиметрическую задачу, применяя различные теоретические знания курса геометрии;
умение математически грамотно и ясно записать решение, приводя при этом необходимые пояснения и обоснования;
владение широким спектром приёмов и способов рассуждений
Общие сведения об участниках экзамена
Проведение в 2020-2021 учебном году ОГЭ по математике для обучающихся 9-х классов, освоивших образовательные программы основного общего образования осуществлялось на основании единого расписания (утверждено Приказом Министерства просвещения Российской Федерации, Федеральной службы по надзору в сфере образования и науки от 12.04.2021 № 162/471 "Об утверждении единого расписания и продолжительности проведения основного государственного экзамена по каждому учебному предмету, требований к использованию средств обучения и воспитания при его проведении в 2021 году" (зарегистрирован 23.04.2021 № 63222).
В основном государственном экзамене в 2021 году приняли участие 318 выпускников г.Муравленко. 99,7% выпускников муниципального образования г. Муравленко успешно преодолели минимальный тестовый порог.
Общие результаты выполнения экзаменационной работы по ОО и классам
|
| качество | успеваемость | «2» | «3» | «4» | «5» | кол-во | Педагог |
| МБОУ «Школа №1 им. В.И.Муравленко» |
|
|
|
|
|
|
|
|
| 9А | 66,7% | 100,0% | 0 | 8 | 15 | 1 | 24 | Мерзлякова И.И. |
| 9Б | 43,5% | 100,0% | 0 | 13 | 8 | 2 | 23 | Осипова Е.В. |
| 9В | 55,0% | 100,0% | 0 | 9 | 11 | 0 | 20 | Осипова Е.В. |
| 9Г | 8,3% | 100,0% | 0 | 11 | 1 | 0 | 12 | Нагорняк Е.П. |
|
| 48,1% | 100% | 0(0%) | 41(51,9%) | 35(44,3%) | 3(3,8%) | 79 | Средний балл по предмету – 3,5 |
| МБОУ «Школа №2» |
|
|
|
|
|
|
|
|
| 9А | 40,9% | 100,0% | 0 | 13 | 7 | 2 | 22 | Зикирин К.М. |
| 9Б | 13,6% | 95,5% | 1 | 18 | 3 | 0 | 22 | Зикирин К.М. |
|
| 27,2% | 97,7% | 1(2,3%) | 31(70,4%) | 10(22,7%) | 2(4,5%) | 44 | Средний балл по предмету – 3,29 |
| МБОУ «Школа №3 им. Покрышкина» |
|
|
|
|
| |
|
|
| 9А | 56,3% | 100,0% | 0 | 7 | 6 | 3 | 16 | Тимощук Л.Э. |
| 9Б | 47,1% | 100,0% | 0 | 9 | 8 | 0 | 17 | Куликова И.А. |
|
| 51,5% | 100% | 0(0%) | 16(48,4%) | 14(42,4%) | 3(9,1%) | 33 | Средний балл по предмету – 3,6 |
| МБОУ «Школа №4» |
|
|
|
|
|
|
|
|
| 9А | 63,6% | 100,0% | 0 | 8 | 12 | 2 | 22 | Кодинцева А.А. |
| 9Б | 71,4% | 100,0% | 0 | 4 | 10 | 0 | 14 | Осипенко Н.В. |
| 9В | 77,3% | 100,0% | 0 | 5 | 14 | 3 | 22 | Заиченко Н.Н. |
| 9Г | 54,5% | 100,0% | 0 | 10 | 6 | 6 | 22 | Кодинцева А.А. |
|
| 66,25 | 100% | 0(0%) | 27(33,75%) | 42(52,5%) | 11(13,75%) | 80 | Средний балл по предмету – 3,8 |
| МБОУ «Школа №5» |
|
|
|
|
|
|
|
|
| 9А | 45,5% | 100,0% | 0 | 12 | 9 | 1 | 22 |
|
| 9Б | 47,4% | 100,0% | 0 | 10 | 8 | 1 | 19 |
|
| 9В | 26,3% | 100,0% | 0 | 14 | 5 | 0 | 19 |
|
| 9Г | 59,1% | 100,0% | 0 | 9 | 7 | 6 | 22 |
|
|
| 45% | 100% | 0 | 45(54,8%) | 29(35,3%) | 8(9,7%) | 82 | Средний балл по предмету – 3,55 |
| ИТОГО |
|
| 1 | 160(50,3%) | 130(40,8%) | 27(8,4%) | 318 | Средний балл по предмету – 3,57 |
Исходя из данных таблицы, можно констатировать следующее:
- отметку неудовлетворительно» получили 1 девятиклассник (МБОУ «Школа №2»), что составляет 0,03% от общего количества участников ОГЭ по математике;
- наибольшее количество девятиклассников, 160 человек, получили отметку «удовлетворительно», что составляет 50,3% из них наибольшее количество в МБОУ «Школа №2» - 70,4%);
- отметку «хорошо» получили 130 человек - это 40,9% участников( наилучшие результаты показала МБОУ «Школа №4» - 52,5%);
- отметку «отлично» получили 27 девятиклассников, что составляет 8,5% от общего количества участников процедуры из них наилучший результат в МБОУ «Школа №4» - 13,75%).
Средняя оценка по предмету «Математика» - 3,57 (наивысший средний балл -3,8(МБОУ «Школа №4», наименьший средний балл – 3,29 в МБОУ «Школа №2»).
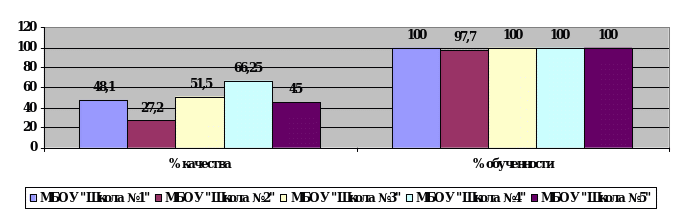Исходя из данных диаграммы, можно констатировать следующее:
-процент качества выполнения работы по математике варьируется от 27,2% (МБОУ «Школа №2») до 66,25% (МБОУ «Школа №4»); процент обученности от 97,7% (МБОУ «Школа №2» до 100% (МБОУ «Школа №1 им. В.И.Муравленко», МБОУ «Школа №3 им. Покрышкина», МБОУ «Школа №4», МБОУ «Школа №5»).
Средние результаты выполнения заданий теста ОГЭ:
| № | Задание | Уровень | Проверяемые элементы содержания | МБОУ «Школа №1 им. В.И.Муравленко» | МБОУ «Школа №2» | МБОУ «Школа №3 им.Покрышкина » | МБОУ «Школа №4» | МБОУ «Школа №5» | По МО |
| ООО | |||||||||
| 1 | 1 | Б | 1. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 100,00% | 93,18% | 93,94% | 98,75% | 95,12% | 96,86% |
| 2 | 2 | Б | 2. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 43,04% | 45,45% | 45,45% | 56,25% | 37,80% | 45,60% |
| 3 | 3 | Б | 3. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 59,49% | 65,91% | 54,55% | 80,00% | 71,95% | 68,24% |
| 4 | 4 | Б | 4. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 40,51% | 29,55% | 33,33% | 48,75% | 37,80% | 39,62% |
| 5 | 5 | Б | 5.Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 79,75% | 79,55% | 75,76% | 76,25% | 78,05% | 77,99% |
| 6 | 6 | Б | 6.Уметь выполнять вычисления и преобразования | 79,75% | 79,55% | 75,76% | 76,25% | 78,05% | 77,99% |
| 7 | 7 | Б | 7. Уметь выполнять вычисления и преобразования | 70,89% | 70,45% | 90,91% | 91,25% | 81,71% | 80,82% |
| 8 | 8 | Б | 8. Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений | 92,41% | 59,09% | 96,97% | 92,50% | 86,59% | 86,79% |
| 9 | 9 | Б | 9.Уметь решать уравнения, неравенства и их системы | 70,89% | 47,73% | 84,85% | 82,50% | 73,17% | 72,64% |
| 10 | 10 | Б | 10. Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 84,81% | 72,73% | 93,94% | 93,75% | 81,71% | 85,53% |
| 11 | 11 | Б | 11. Уметь строить и читать графики функций | 77,22% | 75,00% | 78,79% | 83,75% | 84,15% | 80,50% |
| 12 | 12 | Б | 12. Осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами | 88,61% | 63,64% | 84,85% | 92,50% | 71,95% | 81,45% |
| 13 | 13 | Б | 13. Уметь решать уравнения, неравенства и их системы | 56,96% | 52,27% | 75,76% | 70,00% | 63,41% | 63,21% |
| 14 | 14 | Б | 14. Уметь строить и читать графики функций, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 69,62% | 45,45% | 72,73% | 80,00% | 63,41% | 67,61% |
| 15 | 15 | Б | 15. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 87,34% | 81,82% | 87,88% | 91,25% | 93,90% | 89,31% |
| 16 | 16 | Б | 16. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 86,08% | 56,82% | 87,88% | 92,50% | 86,59% | 83,96% |
| 17 | 17 | Б | 17. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 84,81% | 86,36% | 87,88% | 80,00% | 81,71% | 83,33% |
| 18 | 18 | Б | 18. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 100,00% | 100,00% | 100,00% | 100,00% | 100,00% | 100,00% |
| 19 | 19 | Б | 19. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | 74,68% | 75,00% | 78,79% | 83,75% | 85,37% | 80,19% |
| 20 | 20 | П | 20. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы | 18,99% | 5,68% | 24,24% | 31,25% | 10,37% | 18,55% |
| 21 | 21 | П | 21. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 5,70% | 4,55% | 12,12% | 13,75% | 10,98% | 9,59% |
| 22 | 22 | П | 22. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 0,63% | 1,14% | 9,09% | 1,25% | 1,83% | 2,04% |
| 23 | 23 | П | 23. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 3,16% | 3,41% | 10,61% | 7,50% | 8,54% | 6,45% |
| 24 | 24 | П | 24. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | 0,63% | 0,00% | 0,00% | 10,63% | 1,22% | 3,14% |
| 25 | 25 | П | 25. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 1,90% | 0,00% | 1,52% | 4,38% | 1,22% | 2,04% |
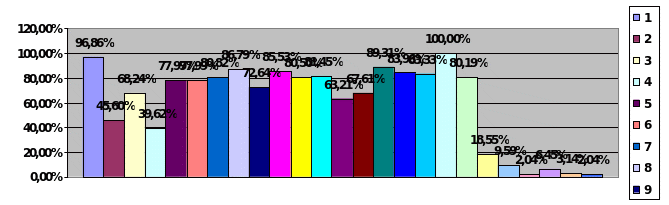
Средний процент выполнения заданий с кратким ответом базового уровня сложности в диапазоне от 39,62% до 100%.
У большинства участников ОГЭ вызвали затруднения задания повышенного уровня сложности, назначение которых дифференцировать хорошо успевающих школьников. Эти задания из различных разделов курса математики. Средний процент выполнения заданий повышенного уровня сложности составил в диапазоне от 2,04% до 18,55%).
Анализ представленных результатов выполнения заданий c кратким ответом базового и повышенного уровней сложности контрольной работы по математике позволяет сделать вывод о том, что участники ОГЭ по математике 2021 года показали удовлетворительный уровень сформированности базовых знаний и умений при выполнении заданий базового уровня сложности и низкий уровень при выполнении заданий повышенного и высокого уровней сложности.
Наиболее сложными для участников ОГЭ по математике оказались задания 2-5. Типичными ошибками при выполнении этих заданий являются:
- невнимательное чтение текста задачи;
- ошибки вычислительного характера;
- неумение применять математические знания простейших практических ситуациях.
Сложным оказалось задание 13 на умение решать уравнения, неравенства и их системы.. Для отработки навыков решения задач такого типа необходимо использовать пособия, включенные в размещенный на сайте ФИПИ (www.fipi.ru) перечень учебных пособий, разработанных с участием ФИПИ.
Диаграмма распределения первичных баллов участников ОГЭ по математике в 2021 г.
Реестр затруднений выпускников 2021 учебного года:
| № | Задание | Уровень | Проверяемые элементы содержания | МБОУ «Школа №1 им. В.И.Муравленко» | МБОУ «Школа №2» | МБОУ «Школа №3 им.Покрышкина » | МБОУ «Школа №4» | МБОУ «Школа №5» | По МО |
| ООО | |||||||||
| 2 | 2 | Б | 2. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 43,04% | 45,45% | 45,45% | 56,25% | 37,80% | 45,60% |
| 4 | 4 | Б | 4. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | 40,51% | 29,55% | 33,33% | 48,75% | 37,80% | 39,62% |
| 13 | 13 | Б | 13. Уметь решать уравнения, неравенства и их системы | 56,96% | 52,27% | 75,76% | 70,00% | 63,41% | 63,21% |
| 20 | 20 | П | 20. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы | 18,99% | 5,68% | 24,24% | 31,25% | 10,37% | 18,55% |
| 21 | 21 | П | 21. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 5,70% | 4,55% | 12,12% | 13,75% | 10,98% | 9,59% |
| 22 | 22 | П | 22. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 0,63% | 1,14% | 9,09% | 1,25% | 1,83% | 2,04% |
| 23 | 23 | П | 23. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 3,16% | 3,41% | 10,61% | 7,50% | 8,54% | 6,45% |
| 24 | 24 | П | 24. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | 0,63% | 0,00% | 0,00% | 10,63% | 1,22% | 3,14% |
| 25 | 25 | П | 25. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 1,90% | 0,00% | 1,52% | 4,38% | 1,22% | 2,04% |
Реестр затруднений педагогов:
| Затруднение учащихся | Затруднение педагогов |
| 2. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Методика формирования умения: -выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели - выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели - решать уравнения, неравенства и их системы - выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы - выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели повышенной сложности - выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели повышенной сложности - выполнять действия с геометрическими фигурами, координатами и векторами повышенной сложности - доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения повышенной сложности -выполнять действия с геометрическими фигурами, координатами и векторами повышенной сложности |
| 4. Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | |
| 13. Уметь решать уравнения, неравенства и их системы | |
| 20. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы повышенной сложности | |
| 21. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели повышенной сложности | |
| 22. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели повышенной сложности | |
| 23. Уметь выполнять действия с геометрическими фигурами, координатами и векторами повышенной сложности | |
| 24. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | |
| 25. Уметь выполнять действия с геометрическими фигурами, координатами и векторами повышенной сложности |
Сравнительная характеристика выполнения заданий выпускниками 2021 г., 2019 г. и 2018 г.:
| № | Задание | Уровень | Проверяемые элементы содержания | Итого 2021 год* | Итого 2019 год | Итого 2018 год | Динамика |
| 1 | 1 | Б | Уметь выполнять вычисления и преобразования | 77,99% | 72,91% | 78,30% | +5,08% |
| 2 | 2 | Б | Пользоваться основными единицами длины, массы, времени, скорости, площади, объёма; выражать более крупные единицы через более мелкие и наоборот |
| 94,52% | 86,79% | - |
| 3 | 3 | Б | Уметь выполнять вычисления и преобразования | 80,82 | 95,39% | 90,25% | -14,57% |
| 4 | 4 | Б | Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений | 86,79% | 80,40% | 80,82% | +6,39% |
| 5 | 5 | Б | Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимо- стей |
| 91,93% | 92,45% | - |
| 6 | 6 | Б | Уметь решать уравнения, неравенства и их системы | 72,64% | 78,67% | 78,93% | -6,03% |
| 7 | 7 | Б | Решать несложные практические расчетные задачи; решать задачи,связанные с отношением, пропорциональностью величин, дробями,процентами; пользоваться оценкой и прикидкой при практических расчетах; интерпретировать результаты решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых объектов |
| 84,73% | 70,75% | - |
| 8 | 8 | Б | Анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках |
| 97,69% | 100,00% | - |
| 9 | 9 | Б | Решать практические задачи, требующие систематического перебора ариантов; сравнивать шансы наступления случайных событий, оценивать вероятности случайного события, сопоставлять и исследовать модели реальной ситуацией с использованием аппарата вероятности и статистики | 85,53% | 85,59% | 92,14% | -0,06% |
| 10 | 10 | Б | Уметь строить и читать графики функций | 67,61% | 81,56% | 85,85% | -13,95% |
| 11 | 11 | Б | Уметь строить и читать графики функций |
| 54,18% | 89,94% | - |
| 12 | 12 | Б | Уметь выполнять преобразования алгебраических выражений |
| 46,11% | 70,75% | - |
| 13 | 13 | Б | Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами | 81,45% | 67,72% | 72,01% | +13,73% |
| 14 | 14 | Б | Уметь решать уравнения, неравенства и их системы | 63,21% | 62,82% | 62,26% | +0,39% |
| 15 | 15 | Б | Описывать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, решать практические задачи, связанные с нахождением геометрических величин | 89,31% | 88,18% | 80,82% | +1,13% |
| 16 | 16 | Б | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 83,96% | 94,24% | 88,68% | -10,28% |
| 17 | 17 | Б | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 83,33% | 80,98% | 50,31% | +2,35% |
| 18 | 18 | Б | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 100% | 89,63% | 86,48% | +10,37% |
| 19 | 19 | Б | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
| 85,01% | 98,11% | - |
| 20 | 20 | Б | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | 80,19% | 67,72% | 75,47% | +12,47% |
| 21 | 21 | П | Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций | 18,99% | 27,38% | 18,08% | -8,39% |
| 22 | 22 | П | Уметь выполнять преобразования алгебраических выражений, решатьуравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 5,7% | 15,85% | 5,97% | -10,15% |
| 23 | 23 | П | Уметь выполнять преобразования алгебраических выражений, решатьуравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | 0,63% | 2,02% | 2,20% | -1,39% |
| 24 | 24 | П | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 3,16% | 14,27% | 21,70% | -11,11% |
| 25 | 25 | П | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные за- ключения | 0,63% | 6,05% | 13,36% | -5,42 |
| 26 | 26 | П | Уметь выполнять действия с геометрическими фигурами, координатами и векторами | 1,9% | 0,00% | 0,00% | +1,9% |
*Особенности проведения ГИА в 2020 году были обусловлены мероприятиями, направленными на обеспечение санитарно-эпидемиологического благополучия населения и предотвращение распространения новой коронавирусной инфекции (COVID-19).
В 2019/20 учебном году выпускники 9-х классов получили аттестаты об основном общем образовании на основании приказа Минпросвещения от 11.06.2020 № 295 «Об особенностях заполнения и выдачи аттестатов об основном общем и среднем общем образовании в 2020 году». Оценки в аттестатах выставлены как среднее арифметическое четвертных отметок за 9-й класс целыми числами в соответствии с правилами математического округления.
Федеральный институт педагогических измерений (ФИПИ) утвердил изменения в Основной государственный экзамен 2020 года. Теперь у учеников проверяются не только знания, но и умение их применять. В задания по математике включен новый блок практико-ориентированных задач 1-5.
Выполнение заданий группы Б свидетельствует о наличии у выпускника общематематических навыков, необходимых человеку в современном обществе. Задания этой̆ группы проверяют базовые вычислительные, логические умения и навыки, умение анализировать информацию, представленную в графиках и таблицах, умение использовать простейшие вероятностные и статистические модели, умение ориентироваться в простейших геометрических конструкциях. Элемент содержания считается усвоенным на базовом уровне, если с соответствующим заданием справляются не менее 65% выпускников.
Представленные данные говорят о том, что количество заданий базового уровня выполняемость которых ниже указанного уровня в 2021 году это задания № 2 (Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели), № 4 (Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели), xто на одно задание меньше, чем в 2019 году (в 2019 году – это задания № 11,12 (Уметь строить и читать графики функций), № 14 (Уметь решать уравнения, неравенства и их системы). В 2018 году таких заданий было 2 - № 14 (Уметь решать уравнения, неравенства и их системы), № 17 (Уметь выполнять действия с геометрическими фигурами, координатами и векторами):
| 2021 год | 2019 год | 2018 год |
| № 2 (Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели), | № 11 (Уметь строить и читать графики функций) | № 14 (Уметь решать уравнения, неравенства и их системы) |
| № 4 (Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели), | №12 (Уметь строить и читать графики функций) | № 17 (Уметь выполнять действия с геометрическими фигурами, координатами и векторами) |
| - | № 14 (Уметь решать уравнения, неравенства и их системы). | - |
Рекомендации педагогам:
1. При подготовке к уроку тщательно продумывать ход изложения материала, правильность и точность всех формулировок; грамотно оформлять все виды записей.
2. Уделять внимание на каждом уроке формированию метапредметных умений и навыков, в том числе умению анализировать, сравнивать, сопоставлять, приводить необходимые доказательства, делать выводы и обобщения. Учить школьников работать с книгой, справочной литературой («найдите в параграфе …», «что означает это слово…», «о чем идет речь в данном абзаце…», «что должен содержать ответ на поставленный вопрос…» и т.п.).
3. Систематически проводить работу по обогащению и конкретизации словаря учащихся, по ознакомлению с терминологией изучаемого предмета. При объяснении новых терминов - слова четко произносить, записывать на доске и в тетрадях, постоянно проверять усвоение их значения и правильное употребление. Использовать таблицы, плакаты с трудными по написанию и произношению словами, относящимися к данной учебной дисциплине, к данному разделу программы.
4. Добиваться повышения культуры устной разговорной речи учащихся.
5. Шире использовать все формы внеклассной работы (олимпиады, конкурсы, факультативные и кружковые занятия, диспуты, собрания и т. п.) для совершенствования речевой культуры учащихся.
6. При подготовке к уроку тщательно продумывать ход изложения материала, правильность и точность всех формулировок; грамотно оформлять все виды записей.
7.При объяснении нового материала использовать наглядность, образцы записей, таблицы, технические средства обучения.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
