Глава 2.
Методический анализ результатов ОГЭ
по учебному предмету
«Математика»
(наименование учебного предмета)
Далее приведена типовая структура отчета по учебному предмету
2.1. Количество участников ОГЭ по учебному предмету (за последние 3 года1)
Таблица 1
| Участники ОГЭ | 2019 | 2021 | 2022 |
| чел. | % 2 | чел. | % | чел. | % |
| Выпускники текущего года, обучающихся по программам ООО |
|
|
|
| 57 | 100 |
| Обучающиеся на дому |
|
|
|
| 0 | 0 |
| Участники с ограниченными возможностями здоровья |
|
|
|
| 0 | 0 |
ВЫВОД о характере изменения количества участников ОГЭ по предмету (отмечается динамика количества участников ОГЭ по предмету в целом, по отдельным категориям, видам образовательных организаций)
2.2. Основные результаты ОГЭ по учебному предмету «Математика»
2.2.1. Диаграмма распределения первичных баллов участников ОГЭ по предмету в 2022 г.
(количество участников, получивших тот или иной балл)
Участников ОГЭ, набравших от 0 до 7 баллов, нет.
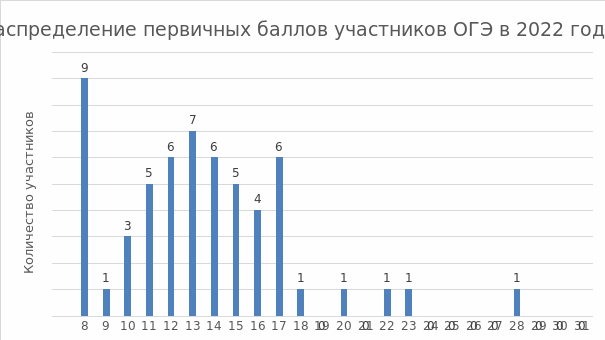
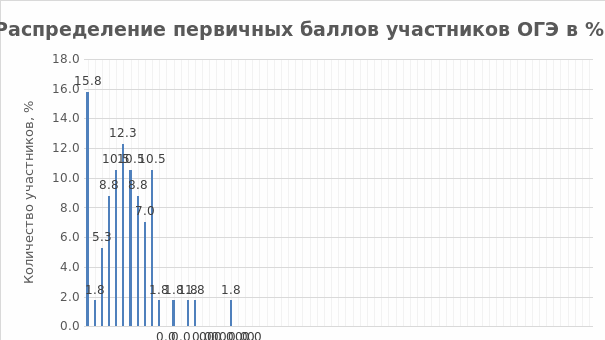
2.2.2. Динамика результатов ОГЭ по предмету
Таблица 5
|
| 2019 г. | 2021 г. | 2022 г. |
| чел. | %3 | чел. | % | чел. | % |
| Получили «2» |
|
|
|
| 0 | 0 |
| Получили «3» |
|
|
|
| 37 | 65 |
| Получили «3» преодолевшие порог на 1-2 балла |
|
|
|
| 28 | 49 |
| Получили «4» |
|
|
|
| 17 | 30 |
| Получили «5» |
|
|
|
| 3 | 5 |
| Получили «5» с запасом 1-2 балла от установленной границы |
|
|
|
| 2 | 4 |
| Получили «5» набравших максимальный балл |
|
|
|
| 0 | 0 |
2.2.3. ВЫВОДЫ о характере результатов ОГЭ по предмету в 2022 году и в динамике.
В соответствии с диаграммой распределения первичных баллов 15,8% (пиковое значение диаграммы) обучающихся набрали 8 баллов из 31 возможного количества баллов (пороговое значение для успешной сдачи экзамена).
Средний первичный балл в 2022 году составил 13 баллов, средняя отметка составила 3,4. Качество знаний составило 35%, а уровень обученности - 48%. Максимальный балл в 2022 году составил 28 баллов.
2.3. Анализ результатов выполнения отдельных заданий или групп заданий по предмету
2.3.1. Краткая характеристика КИМ по предмету
Работа содержит 25 заданий и состоит из двух частей. Часть 1 содержит 19 заданий с
кратким ответом, часть 2–6 заданий с развернутым ответом.
Часть 1 направлена на проверку базовой математической компетентности, а часть 2 – на
проверку владения материалом на повышенном и высоком уровнях.
Назначение части 1 – проверить владение основными алгоритмами, знание и понимание
ключевых элементов содержания (математических понятий, их свойств, приёмов решения задачи т. п.), умение пользоваться математической записью, применять знания к решению
математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.
По разделам содержания части 1:
Числа и вычисления – 7 заданий;
Алгебраические выражения – 1 задание;
Уравнения и неравенства – 2 задания;
Числовые последовательности – 1 задание;
Функции и графики – 1 задание;
Координаты на прямой и плоскости – 1 задание;
Геометрия – 5 заданий;
Статистика и теория вероятностей – 1 задание.
Назначение части 2 - дифференцировать хорошо успевающих школьников по уровням подготовки, выявить наиболее подготовленную часть выпускников, составляющую потенциальный контингент профильных классов. Она содержит задания повышенного уровня сложности из различных разделов курса математики.
Все задания части 2 требуют записи решений ответа и направлены на проверку таких качеств математической подготовки, как:
Уверенное владение формально-оперативным алгебраическим аппаратом;
Умение решать комплексную задачу, включающую в себя знания из различных тем курса алгебры;
Умение решить планиметрическую задачу, применяя теоретические знания курса
геометрии;
Умение математически грамотно и ясно записать решения, приводя при этом
необходимые пояснения и обоснования;
Владение широким спектром приёмов и способов рассуждений.
По разделам содержания части 2:
Уравнения и неравенства – 2 задания;
Функции и графики – 1 задание;
Геометрия – 3 задания.
Всего в работе 25 заданий, из которых 19 заданий базового уровня, 4 задания
повышенного уровня и 2 задания высокого уровня.
2.3.2. Статистический анализ выполняемости заданий / групп заданий КИМ ОГЭ по
учебному предмету в 2022 году
В обобщенном плане КИМ по математике приведены средние проценты выполнения по каждой группе выпускников.
| Номер задания в КИМ |
Проверяемые элементы содержания / умения | Уровень сложности задания | Средний процент выполнения | Процент выполнения в группах, получивших отметку |
| «3» | «4» | «5» |
|
|
1 | Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
87,7 |
81,1 |
100 |
100 |
|
|
2 | Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
33,3 |
8,8 |
70,6 |
33,3 |
|
|
3 | Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
36,8 |
18,9 |
64,7 |
100 |
|
|
4 | Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
28,1 |
10,8 |
52,9 |
100 |
|
|
5 | Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
21 |
2,7 |
47,1 |
100 |
|
|
6 | Уметь выполнять вычисления и преобразования |
Б |
93 |
89,2 |
100 |
100 |
|
|
7 | Уметь выполнять вычисления и преобразования |
Б |
86 |
78,4 |
100 |
100 |
|
|
8 | Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений |
Б |
93 |
89,2 |
100 |
100 |
|
| 9 | Уметь решать уравнения, неравенства, их системы | Б | 98,2 | 97,3 | 100 | 100 |
|
|
10 | Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
73,7 |
62,2 |
94 |
100 |
|
| 11 | Уметь строить и читать графики функций | Б | 71,9 | 62,2 | 88,2 | 100 |
|
|
12 | Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами |
Б |
47,4 |
24,3 |
88,2 |
100 |
|
| 13 | Уметь решать уравнения, неравенства, их системы | Б | 84,2 |
78,4 |
94,1 |
100 |
|
|
14 | Уметь строить и читать графики функций, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
20,8 |
32,4 |
64,7 |
100 |
|
|
15 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
92,9 |
89,2 |
100 |
100 |
|
|
16 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
70,2 |
56,8 |
94,1 |
100 |
|
|
17 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
82,5 |
78,4 |
88,2 |
100 |
|
|
18 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
82,5 |
73 |
100 |
100 |
|
|
19 | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные рассуждения правильность рассуждений, распознавать ошибочные рассуждения |
Б |
59,6 |
46 |
82,4 |
100 |
|
|
20 | Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства, их системы |
П |
1,8 |
0 |
0 |
33,3 |
|
|
21 | Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства, их системы, строить и читать графики функций, строить и исследовать простейшие математические модели |
П |
8,8 |
3,5 |
0 |
100 |
|
|
22 | Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства, их системы, строить и читать графики функций, строить и исследовать простейшие математические модели |
В |
1,8 |
0 |
0 |
33,3 |
|
|
23 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П |
7 |
0 |
5,9 |
100 |
|
|
24 | Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные рассуждения |
П |
1,8 |
0 |
0 |
33,3 |
|
|
25 | Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
В |
0 |
0 |
0 |
0 |
|
В 2020-2021 учебном году в связи со сложной эпидемиологической обстановкой обучение проводилось в смешанном формате – очной и дистанционной формах, в связи с этим сравнение результатов ОГЭ по математике в 2022, 2021 и 2019 годах необходимо проводить с учётом этих обстоятельств.
Проведем анализ выполнения части 1 по разным группам, выделив согласно спецификации КИМ 2022 года проценты выполнения: ниже 60%, от 60% до 69%, от 70% до 79%, от 80% до 90%.
Проценты выполнения ниже 60% у заданий №№2,3,4,5,12,14,19;
от 60% до 69% - нет;
от 70% до 79% - у заданий №№10,11,16;
выше 80% - у заданий №№1,6,7,8, 9, 13, 15, 17, 18.
В группе обучающихся, получивших отметку «3», проценты выполнения
ниже 60% у заданий №№2,3,4,5,12,14,16,19;
от 60% до 69% - у заданий №№10,11;
от 70% до 79% - у заданий №№7,13, 17, 18;
выше 80% - у заданий №№1,6,8,9,15.
В группе обучающихся, получивших отметку «4», проценты выполнения
ниже 60% - у заданий №№4, 5;
от 60% до 69% - у заданий №№3,14;
от 70% до 79% - только у задания №2;
выше 80% - у заданий №№1,6,7,8,9,10,11,12,13,15,16,17,18,19.
В группе обучающихся, получивших отметку «5», проценты выполнения
ниже 60% - только у задания №2
выше 80% - у всех остальных. Эта группа справилась со всеми заданиями части 1.
В группе обучающихся, получивших отметку «3», один выпускник получил баллы за часть 2. Средний процент выполнения заданий этой части близок к нулю.
В группе обучающихся, получивших отметку «4», также один выпускник справился с заданиями №21 и №23.
В группе обучающихся, получивших отметку «5», два участника ОГЭ справились только с заданиями №21, 23 и один участник с заданиями №20, 21, 22, 23,24.
Таким образом, по части 1 для участников ОГЭ основную сложность вызвали задания №№2,4,5,14. Все они относятся к задачам с практическим содержанием в прикладных ситуациях. У учащихся вызывает сложности построение простейших моделей прикладных задач вместо использования заученных алгоритмов в стандартных ситуациях. Это говорит о практике применения и заучивания готовых схем без понимания. Для устранения таких трудностей надо активнее внедрять практико- ориентированные задачи в проверку базовых математических умений.
Вероятными причинами затруднений и типичных ошибок участников экзамена являлись:
Снижение уровня вычислительной культуры.
«Натасканность» на алгоритмы решения задач в ущерб пониманию.
Недостаточная самодисциплина некоторых обучающихся при дистанционном формате обучения.
В КИМ 2022 года присутствовал блок практико-ориентированных задач (№№1-5), объединенных одной прикладной темой, для успешного выполнения заданий этого блока обучающимся необходимо обладать достаточным уровнем читательской грамотности. Неумение выбирать нужную информацию из большого массива прозаического текста, неумение сопоставлять информацию, представленную в разных видах, и, как следствие неумение составлять грамотную математическую модель реальной ситуации не позволило обучающимся получить достаточное количество баллов за эти задания.
Чтобы помочь подготовиться к экзамену группам с разным уровнем подготовки требуется организация дифференцированного обучения. На начальном этапе следует выявить дефициты подготовки и для каждой группы разработать программу их восполнения.
Для групп, претендующей на отметки «4» или «5», рекомендуется сделать упор на геометрические задачи части 2 с развернутым ответом, а также на задание по построению графика (№22). Следует уделять внимание грамотному описанию решений заданий с развернутым ответом. При подготовке к ОГЭ учителям следует ориентировать учащихся, претендующих на отметки «4» и «5», на максимально полное выполнение заданий второй части.
Для группы со слабым уровнем следует детальнее отработать базовые математические навыки, добиваться безошибочного выполнения 12 задач (из которых 3 по геометрии) из заданий части 1. А также для блоков практико-ориентированных задач добиться полного понимания моделей решения.
Следует нацеливать все группы обучающихся на полное выполнение блока заданий первой части.
1� В 2020 г. ОГЭ не проводился, поэтому для анализа берутся результаты ОГЭ 2019г.
2� % - Процент от общего числа участников по предмету
3� % - Процент от общего числа участников по предмету



















