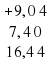Добрый день, уважаемые коллеги! 1.Требования к результатам освоения основной образовательной программы.
Хочу начать свое выступление словами Джон Дьюи: «Если мы будем учить сегодня так, как мы учили вчера, мы украдём у детей завтра». Слайд1,2
С введением новых ФГОС революции в образовании не произошло. Преемственность между стандартными первого и второго поколения определяется на основе единства содержания. Так же, как и в стандартах первого поколения, обоснованы c такие умения, без которых выпускник одной ступени образования не сможет продолжить обучение на следующей. Стандарт поддерживает традиции существующего обучения, но расставляет иные акценты и ориентируется на иные приоритеты. Достоинством стандартов второго поколения можно считать то, что его разработчики попытались представить результат освоения обучающимися основной образовательной программы общего образования тремя группами требований к результатам освоения: личностными, метапредметными и предметными. Слайд 3,4
Как для учеников, так и для Учителя, урок интересен тогда ,когда он современен в самом широком понимании этого слова. Современный – это и совершенно новый, и не теряющий связи с прошлым, одним словом - актуальный. Современный урок – это урок, характеризующийся следующими признаками : Слайд 5
Главной целью урока является развитие каждой личности, в процессе обучения и воспитании.
На уроке реализуется личностно-ориентированный подход к обучению.
На уроке реализуются идеи гуманизации и гуманитаризации образования.
На уроке реализуется деятельностный подход к обучению.
Организация урока динамична и вариативна.
На уроке используются современные педагогические технологии
Главное для учителя в новой системе образования – это управлять процессом обучения, а не передавать знания.
.
2. Основные требования и идеи ФГОС на уроке . Слайд 6
Согласно ФГОС различается, прежде всего, деятельность учителя и учащихся на уроке. Ученик из присутствующего и пассивно исполняющего указания учителя на уроке традиционного типа теперь становится главным деятелем. «Нужно, чтобы дети, по возможности, учились самостоятельно, а учитель руководил этим самостоятельным процессом и давал для него материал» – слова К.Д. Ушинского отражают суть урока современного типа, в основе которого заложен принцип системно– деятельностного подхода.
Педагоги разных стран и эпох всегда искали методические пути превращения учебной деятельности в радостный процесс познания мира, пути развития умственных сил учащихся
Многими педагогами освоены и находят применение различные образовательные технологии: дифференцированное обучение, развивающее обучение, проблемное обучение; модульные технологии; здоровьесберегающие технологии; метод проектов; информационно - коммуникационные технологии и другие. Слайд 7
Согласно высказываниям американского философа, психолога и педагога Джона Дьюи (1859-1952), мыслить человек начинает тогда, когда сталкивается с трудностями, преодоление которых имеет для него большое значение1. Впоследствии, за «трудностями», которые нужно преодолеть, размышляя над поиском решения, закрепилось название «проблем». Правильное построение обучения, по мнению Дьюи, должно быть проблемным.
3. Урок- проблема(загадка). Слайд 8
Обучение детей целеполаганию, формулированию темы и цели урока возможно через создание проблемной ситуации и ведение проблемного диалога. Учитель осуществляет проблемное обучение, если не даёт информацию в готовом виде, а организовывает работу так, что ребята сами открывают новое знания. От учителя требуется лишь правильное использование всех тех ресурсов, которые скрыты в курсе преподаваемого предмета.
На основании обобщения передового опыта можно указать несколько основных приёмов создания проблемных ситуаций: Слайд 9
учитель подводит школьников к противоречию и предлагает им самим найти способ его разрешения;
излагает различные точки зрения на один и тот же вопрос;
сталкивает противоречия практической деятельности;
предлагает классу рассмотреть явление с различных позиций;
побуждает учащихся делать сравнения, обобщения, выводы из ситуации, сопоставлять факты;
ставит конкретные вопросы (на обобщение, обоснования, конкретизацию, логику рассуждения;
определяет проблемные теоретические и практические задания;
ставит проблемные задачи (с недостаточными или избыточными исходными данными; с неопределенностью в постановке вопроса; с противоречивыми данными; с заведомо допущенными ошибками; с ограниченным временем решения; на преодоление психической инерции и другим).
При изучении нового материала я часто использую метод создания проблемных ситуаций. Из всех методов этой технологии я отдаю предпочтение подводящему диалогу. При составлении подводящего к теме диалога я подбираю логическую цепочку посильных ученикам вопросов и заданий, которые пошагово приводят класс к формулированию темы урока. Слайд 10
На уроке математики в 5-ом классе ,при прохождении темы « Сложение и вычитание десятичных дробей», не озвучила тему изначально. Вспомнили сложение и вычитание натуральных чисел, затем дробей с одинаковым знаменателем, смешанных чисел. 775435
+4575
______
780010 5 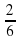 +
+ 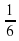 = 5
= 5 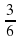 4
4 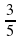 + 11
+ 11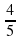 = 16
= 16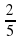
3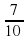 + 5
+ 5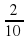 = 8
= 8 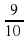 9
9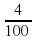 + 7= 16
+ 7= 16 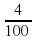
запишем в виде десятичной дроби
3,7 + 5,2 = 8,9; 9,04 + 7 = 16,04
9 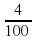 + 7
+ 7 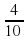 ! или 6
! или 6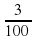 - 4
- 4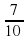 !
!
9,04 + 7,4
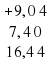
Подвела учеников к теме урока. Слайд 12,13( правила в стихотворной форме)
Тема « Сумма углов треугольника» 7 класс. Так, перед изучением темы о сумме внутренних углов треугольника можно предложить такую задачу: «Построить треугольник по трем заданным углам: Слайд 14,15
1.Углы А=90, В=60, С=45;
2.Углы А=70, В=30, С=50;
3. Углы А=50, В=60, С=70.
Учащиеся, вооружившись линейкой и транспортиром, начинают строить треугольники. В первом случае, построив углы А и В и отложив угол в 45 от луча АС (или ВС, кому как нравится), ребята увидят, что вместо треугольника получается четырехугольник. Во втором случае независимо от того, какие первые два угла школьники выбирают для построения, всегда получается треугольник, третий угол которого либо больше, либо меньше заданного. И только в третьем случае выстраивается треугольник по трем заданным углам. По окончании уже можно выдвинуть предположение о сумме внутренних углов треугольника. Надо отметить и слабые стороны проблемного обучения:
1.Значительно большие расходы времени на изучение учебного материала;
2.Малая эффективность их при усвоении принципиально новых разделов учебного материала, где не может быть применен принцип опоры на прежний опыт;
3.В меньшей мере применимо при изучении сложных тем, где крайне необходимо объяснение учителем, а самостоятельный поиск оказывается недоступным для большинства школьников.
Метод создания проблемных ситуаций позволяет развивать познавательные действия, включающие действия исследования, поиска, отбора и структурирования необходимой информации, моделирование изучаемого содержания.
Осуществляю дифференцированный подход, он способствует развитию индивидуальных способностей, развитию самостоятельного творческого мышления. Разно-уровневые задания облегчают организацию занятия в классе, создают условия для продвижения учащихся в учебе в соответствии с их возможностями. Работая дифференцированно с учащимися, вижу, что их внимание не падает на уроке, так как каждому есть посильное задание, «сильные» ученики не скучают, так как всегда им дается задача, над которой надо думать. Ребята постоянно заняты посильным трудом. Слайд
Например: Тема: «Законы арифметических действий» Слайд 16
1уровень: не выполняя вычислений, сравни значения выражений
23 ∙16 +23 ∙84 и 23∙(16+84)
2уровень: вычисли 23 ∙16 +23 ∙84
3уровень: вычисли 230 ∙16 +23 ∙840
Я думаю, что в данном случае мы развиваем регулятивные действия, обеспечивающие возможность управления познавательной и учебной деятельностью посредством постановки целей.
4. Задачи из жизненных ситуаций. Математическая неделя: игра « Математический поезд» между 5-ми классами. Слайд 17,18
На уроках интерес поддерживаю подборкой задач, приближенных к современной тематике, к жизненному опыту детей, что служит достаточно сильным мотивом для решения предлагаемых задач. Например, на традиционном уроке математики предлагается просто вычислить площадь прямоугольника, на современном же уроке задание может выглядеть иначе: Дан план комнаты и размеры напольных покрытий полностью закроет пол. Выполняя такие задания, обучающиеся применят имеющиеся знания в новой ситуации, связанной с реальной жизнью.
Практикую различные виды контроля (зачет по теории и практике, самостоятельная работа контролирующего характера, проекты, презентации). Для подготовки к зачету учащимся предлагается открытый перечень теоретических вопросов и практических задач, разноуровневые задания для подготовки к итоговому уроку. Тем самым каждый ученик может оценить свои знания по изученной теме, что способствует развитию правильной самооценке.
5. Межпредметная связь.
Очень многие педагоги констатируют, что современные дети труднее поддаются обучению, чем поколение их старших братьев или, тем более, советских школьников, что у школьников сузился кругозор, дети так и говорят: зачем нам это? То, что нашему поколению было естественно знать в 5-6 классе – например, столицы крупнейших стран, личности из истории,- этого не знают даже старшеклассники : «Нам этого не надо», утверждают они. Соответственно , сегодняшние дети никак не менее информационно развиты. Просто они более прагматичны , и у них в голове задерживаются только те сведения и знания , про которые они понимают: зачем им надо. В эпоху Интернета у школьников возникает «клиповое мышление», динамичной и дозированной подачи материала в форме гипертекста. Учитывая особенности мышления современных школьников, преимущество будут получать короткие циклы занятий и тренингов с обязательными межпредметными связями. Слайд 19
Учителю математики приходится иметь дело с тремя видами межпредметных временных связей: предшествующими, сопутствующими и перспективными.
предшествующие межпредметные связи – это связи, когда при изучении материала курса математики опираются на ранее полученные знания по другим предметам.
сопутствующие межпредметные связи – это связи, учитывающие тот факт, что ряд вопросов и понятий изучаются как по математике, так и по другим предметам.
перспективные межпредметные связи используются, когда изучение материала по математике опережает его применение в других предметах.
В практике работы учителя математики встречаются все эти три вида временных межпредметных связей, но чаще учителя других предметов используют знания учащихся по математике.
Для меня, как учителя математики, при осуществлении межпредметных связей в обучении важное значение имеют отбор для уроков материала, привлекаемого из курсов других учебных дисциплин, и методика его использования. Отбирая для своего урока сведения, которые учащиеся получают при изучении различных предметов, ориентируюсь, прежде всего, на программу и на то, как, в каком объеме эти вопросы представлены в соответствующих школьных учебниках. На основании полученных данных, составляя планы своих урок.
Математика – это системообразующий предмет, который формирует общеучебные умения в других предметах школьной программы химии, физике, биологии. Межпредметная интеграция даёт возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математики как части общечеловеческой культуры. Этому способствуют задания, связанные с историей своей страны.
Математика и история: Сведения из истории математики, исторические задачи сближают эти два школьных предмета. История обогащает математику гуманитарным и эстетическим содержанием, развивает образное мышление учеников. Слайд 20
С большим интересом ребята решают задачи исторического характера. Некоторые итоги Петровских преобразований" посвящена задача на составление уравнения. "В 1795 г. бюджет России составлял 9,75 млн. рублей. Из них 2/3 расходовали на содержание армии и флота. Расходы на флот составляли 0,3 от стоимости содержания армии. Сколько стоило России содержание армии и флота в 1725 г.?" .Дома ребятам предлагается на основе современных статистических данных составить задачу, характерную для нашего времени..
Учащиеся достигнут высоких результатов только тогда, когда увидят, что определённые умения необходимы ему и на других предметах.
Таким образом, эффективное применение межпредметных связей позволяет сформировать и развивать у учащихся общекультурные, учебно-познавательные, информационные и коммуникативные компетенции, которые являются результатом ФГОС ООО.

Спасибо за внимание. Слайд 21,22,23
1Слайд 11







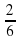 +
+ 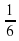 = 5
= 5 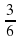 4
4 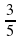 + 11
+ 11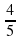 = 16
= 16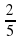
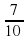 + 5
+ 5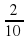 = 8
= 8 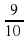 9
9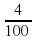 + 7= 16
+ 7= 16 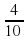 ! или 6
! или 6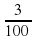 - 4
- 4