Реферат потеме: « разработка предложения по использованию электронной вычислительной техники при изучении математике.»
| Раздел математики | «Неравенства. Системы неравенств с двумя переменными.» |
| Класс | 9 |
| Профиль | Общеобразовательный |
| Тема курса | «Системы неравенств с двумя переменными.» |
Технологии: Информационно-коммуникативные технологии.
Оборудование: Компьютер; проектор, интерактивная доска; программа «Advanced Grapher», классная доска; учебник «Алгебра 9 класс». (Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. Москва «Просвещение», 2011г.),
Цели:
Образовательные – повторить понятие решения системы неравенств с двумя переменными; формировать умение решать системы неравенств с двумя переменными, отработать навыки построения множества решений систем неравенств на координатной плоскости;
Развивающие – формирование графической и функциональной культуры учащихся;
Воспитательные – воспитание интереса к математике и повышение мотивации учебной деятельности через внедрение компьютерных технологий в процесс обучения, побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.
Ход занятия
Повторение и закрепление пройденного материала:
- Что называется решением системы неравенств с двумя переменными?
- как изображается на плоскости множество решений системы неравенств с двумя переменными?
- Что может представлять собой множество решений системы? (сегмент, угол, полоса и т.д.)
Учитель. Давайте повторим алгоритм решения системы неравенств с двумя переменными:
Пусть мы имеем неравенство с двумя переменными одного из следующих видов:
y f(x); y ≥ f(x); y
Для изображения множества решений такого неравенства на координатной плоскости поступают следующим образом:
1. Строим график функции y = f(x), который разбивает плоскость на две области.
2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.
Пример 1

Ребята в тетрадях рисуют графики функций, а учитель поэтапно показывает графики на интерактивной доске .

Как можно проверить правильно ли показано множество решений? [Правило пробной точки]
Пример 2. Выполнение в тетради, затем поэтапная проверка на интерактивной доске


Пример 3 Выполнение в тетради, затем поэтапная проверка на интерактивной доске.


Пример 4.
Изобразить область, заданную на координатной плоскости системой
{уx2 +2;
{y+x1;
{ x2 + y2 ≤ 9.
Решение.
Строим для начала графики следующих функций
y = x2 + 2 – парабола,
y + x = 1 – прямая
x2 + y2 = 9 – окружность.
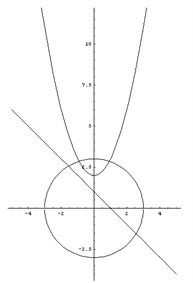
Теперь разбираемся с каждым неравенством в отдельности.
1) y x2 + 2.
Берем точку (0; 5), которая лежит выше графика функции.
Проверяем неравенство: 5 02 + 2 – верно.
Следовательно, все точки, лежащие выше данной параболы y = x2 + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.
2) y + x 1.
Берем точку (0; 3), которая лежит выше графика функции.
Проверяем неравенство: 3 + 0 1 – верно.
Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют второму неравенству системы. Закрасим их зеленой штриховкой.
3) x2 + y2 ≤ 9.
Берем точку (0; -4), которая лежит вне окружности x2 + y2 = 9.
Проверяем неравенство: 02 + (-4)2 ≤ 9 – неверно.
Следовательно, все точки, лежащие вне окружности x2 +y2 =9, 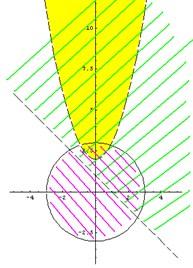 не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром.
Пример 5
Изобразим множество точек, которые являются решениями системы неравенств 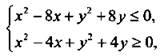 и вычислим площадь этой фигуры.
и вычислим площадь этой фигуры.
Запишем систему неравенств в следующем виде: 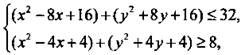 или
или 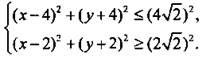
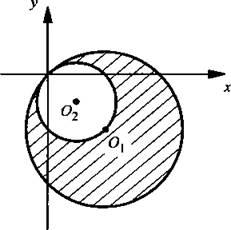
Графиком первого неравенства является круг с центром в точке O1(4; -4) и радиусом 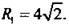 Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O2(2; -2) и радиусом
Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O2(2; -2) и радиусом 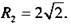 Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).
Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).
Найдем площадь этой фигуры. Она равна разности площадей окружностей: 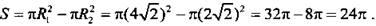 Таким образом, площадь заштрихованной фигуры ровно в 3 раза больше площади малого круга.
Таким образом, площадь заштрихованной фигуры ровно в 3 раза больше площади малого круга.
Литература: «Живая математика.»Москва . Г.Б.Шабат(научный руководитель.)
Алгебра 9 класс. Уч.для общеобразовательных школ. Авторы Ю.Н. Макарычев и др. «Просвещение» 2011 год
Алгебра 8 класс. Уч.для общеобразовательных школ. Авторы Ю.Н. Макарычев и др. «Просвещение» 2011 год
С.С.Минаева «Возможности электронных образовательных ресурсов при обучении математике.» Лекции 1-4 и 5-8. Дистанционные курсы повышения квалификации.
Задача 2.
Изобразить область, заданную на координатной плоскости системой
{уx2 +2;
{y+x1;
{ x2 + y2 ≤ 9.
Решение.
Строим для начала графики следующих функций (рис. 2):
y = x2 + 2 – парабола,
y + x = 1 – прямая
x2 + y2 = 9 – окружность.

Теперь разбираемся с каждым неравенством в отдельности.
1) y x2 + 2.
Берем точку (0; 5), которая лежит выше графика функции.
Проверяем неравенство: 5 02 + 2 – верно.
Следовательно, все точки, лежащие выше данной параболы y = x2 + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.
2) y + x 1.
Берем точку (0; 3), которая лежит выше графика функции.
Проверяем неравенство: 3 + 0 1 – верно.
Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют второму неравенству системы. Закрасим их зеленой штриховкой.
3) x2 + y2 ≤ 9.
Берем точку (0; -4), которая лежит вне окружности x2 + y2 = 9.
Проверяем неравенство: 02 + (-4)2 ≤ 9 – неверно.
Следовательно, все точки, лежащие вне окружности x2 + y2 = 9,  не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром. Получаем следующую картинк Задача 2.
Изобразить область, заданную на координатной плоскости системой
{уx2 +2;
{y+x1;
{ x2 + y2 ≤ 9.
Решение.
Строим для начала графики следующих функций (рис. 2):
y = x2 + 2 – парабола,
y + x = 1 – прямая
x2 + y2 = 9 – окружность.

Теперь разбираемся с каждым неравенством в отдельности.
1) y x2 + 2.
Берем точку (0; 5), которая лежит выше графика функции.
Проверяем неравенство: 5 02 + 2 – верно.
Следовательно, все точки, лежащие выше данной параболы y = x2 + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.
2) y + x 1.
Берем точку (0; 3), которая лежит выше графика функции.
Проверяем неравенство: 3 + 0 1 – верно.
Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют второму неравенству системы. Закрасим их зеленой штриховкой.
3) x2 + y2 ≤ 9.
Берем точку (0; -4), которая лежит вне окружности x2 + y2 = 9.
Проверяем неравенство: 02 + (-4)2 ≤ 9 – неверно.
Следовательно, все точки, лежащие вне окружности x2 + y2 = 9,  не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром. Получаем следующую картинку .
Получаем следующую картинку
Уроки 52-53. Системы неравенств с двумя переменными
Цель: построение решения системы неравенств с двумя переменными на координатной плоскости.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
- Что называется решением системы неравенств с двумя переменными?
- как изображается на плоскости множество решений системы неравенств с двумя переменными?
- Что собой представляет множество решений первой системы? (сегмент)
Второй системы? (угол) Третьей? (полоса)
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Изобразите на координатной плоскости множество точек, задаваемых неравенством.
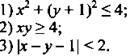
Вариант 2
Изобразите на координатной плоскости множество точек, задаваемых неравенством.
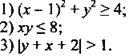
III. Изучение нового материала
В ряде случаев на координатной плоскости приходится изображать множество решений системы неравенств с двумя переменными. Напомним, что пара значений неизвестных, которая одновременно является решением и первого и второго неравенства, называется решением системы двух неравенств с двумя переменными.
Пример 1
Рассмотрим систему неравенств с двумя переменными 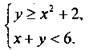
Пара значений переменных (1; 4) является решением системы неравенств, т. к. является решением каждого неравенства: 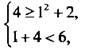 или
или 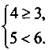
Пара значений переменных (1; 1) не является решением системы неравенств, т. к. не является решением первого неравенства: 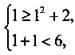 или
или 
Множеством решений системы неравенств с двумя переменными является пересечение множеств решений всех неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.
Пример 2
Изобразим на координатной плоскости множество решений системы неравенств
Первое неравенство системы задает на координатной плоскости круг с центром в начале координат и радиусом, равным 1. Второе неравенство задает полуплоскость, расположенную ниже прямой 2х + у = 0.
Итак, решениями данной системы неравенств являются точки полукруга (они заштрихованы).
Пример 3
На плоскости х0у изобразим точки, удовлетворяющие системе неравенств
Изобразим сначала точки, удовлетворяющие первому неравенству. Построим график границы - график функции у = х2 - 2х - 1. Эта парабола пересекает ось 0у в точке у = -1, ось 0х в точках Вершина параболы находится в точке (1; -2), ветви параболы направлены вверх. Эта кривая разбила координатную плоскость на часть, заключенную между ветвями параболы, и часть, находящуюся за ветвями параболы. Взяв любую точку, например (1; -1), из первой части плоскости, видим, что она удовлетворяет неравенству у х2 - 2х - 1. Поэтому все точки этой части также удовлетворяют неравенству (за исключением границы, т. к. неравенство строгое).
Аналогично, построив границу (х - 1)2 + (у + 2)2 = 1, видим, что неравенству (х - 1)2 + (у + 2)2 ≤ 1 удовлетворяют внутренние и граничные точки окружности.
Штриховкой показаны те точки, которые удовлетворяют системе неравенств. Причем стрелки показывают, что данная граница (часть параболы) не входит в множество решений системы неравенств.
Пример 4
Изобразим множество точек, которые являются решениями системы неравенств 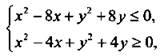 и вычислим площадь этой фигуры.
и вычислим площадь этой фигуры.
Запишем систему неравенств в следующем виде: 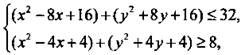 или
или 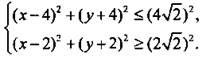

Графиком первого неравенства является круг с центром в точке O1(4; -4) и радиусом 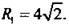 Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O2(2; -2) и радиусом
Графиком второго неравенства являются точки, расположенные за окружностью с центром в точке O2(2; -2) и радиусом 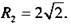 Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).
Итак, решениями данной системы неравенств являются точки, расположенные между двумя касающимися в начале системы координат окружностями (эти точки заштрихованы).
Найдем площадь этой фигуры. Она равна разности площадей окружностей: 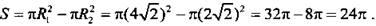 Таким образом, площадь заштрихованной фигуры ровно в 3 раза больше площади малого круга.
Таким образом, площадь заштрихованной фигуры ровно в 3 раза больше площади малого круга.
IV. Задание на уроке
№ 496 (а, б); 497 (б, г); 498 (а); 499 (б); 500 (а, в); 501 (а); 502 (б); 503.
V. Задание на дом
№ 496 (в, г); 497 (а, в); 498 (в); 499 (а); 500 (б, г); 501 (б); 502 (а).
VI. Подведение итогов урока

рок усвоения новых знаний. Алгебра. 9 класс.
Тема: Системы неравенств с двумя переменными.
Цель: Ознакомить обучающихся с понятиями: системы неравенств и решения систем неравенств с двумя переменными; использовать сведения о графиках уравнений с двумя переменными при иллюстрации множеств решений некоторых простейших систем неравенств с двумя переменными; развивать навыки работы в парах, закреплять умение работать с текстом учебника, анализировать прочитанное, выделять главное.
Оборудование: учебник «Алгебра 9» Макарычев Ю.Н., проектор, сканер.
Ход урока
Организационный момент.
Проверка домашнего задания.
два ученика у доски делают рисунок к решению домашнего задания (№487а,б)
остальные выполняют задание:
Какое множество точек задается неравенством: х²+у²-6х-4у+13≤0? (точка(3;2))
проверка работ (с комментариями).
Изучение нового материала.
Целеполагание. Что представляет собой решение неравенства с двумя переменными, вы уже знаете. Как вы полагаете, что будет собой представлять решение системы неравенств такого типа? Целью сегодняшнего урока и будет изучение систем неравенств с двумя переменными и их рашание. Проверить свое предположение вы можете, прочитав раздел учебника по данной теме.
1) Самостоятельная работа обучающихся с текстом учебника (п.22). Ученики первого ряда детально разбирают пример 1: {х²+у²≤4, х+у≥1, второго – пример 2: {у≥х-2, у≥-1.5х+3, третьего – пример 3: {у≤2х+1, у≥2х-2.
2) Проверка понимания прочитанного.
- Что называется решением системы неравенств с двумя переменными?
- как изображается на плоскости множество решений системы неравенств с двумя переменными?
- Что собой представляет множество решений первой системы? (сегмент)
Второй системы? (угол) Третьей? (полоса)
Закрепление.
№496 Является ли решением системы неравенств {х²-2у˃7, 3х+у˃3 пара чисел: (6;-5) – проверяет ученик у доски, (4;2) – ученики первого ряда, (-5;1) – второго, (-2;-1) – третьего. После проверки озвучивают выводы.
№497(а,б)
Работа в парах. Показать штриховкой на координатной плоскости множество решений системы неравенств:
а) {у≥х-3, у≤-х+3;
б) {х-2у˂4, х+у˂3.
Обсудите, к какому виду удобно привести неравенства системы в задании б).
Физминутка.
Ребята выполняют разминку по предотвращению развития сколиоза, а также гимнастику для глаз.
(Во время физминутки учитель сканирует одну из работ обучающихся, вносит ее во флипчарт для возможности коррекции во время анализа)
Проверка выполненных заданий с комментариями и коррекцией (при необходимости).
Дифференцированное закрепление:
Обучающиеся, справившиеся с предыдущим заданием без замечаний, выполняют №500, остальные решают №497 (в,г), комментируя ход решения и делая рисунок на доске.
Домашнее задание.
(Дифференцированное) №498, 504(повт.) или №501 - исследование, 504(повт.)
Итог урока.
Рефлексия. Как вы считаете, цель, поставленная в начале урока, достигнута вами? Из чего складывается решение системы неравенств с двумя переменными? Какие задания вызвали затруднения? Что помогло справиться с ними?
Решение неравенства с двумя переменными, а тем более системы неравенств с двумя переменными, представляется достаточно сложной задачей. Однако есть простой алгоритм, который помогает легко и без особых усилий решать на первый взгляд очень сложные задачи такого рода. Попробуем в нем разобраться.
Пусть мы имеем неравенство с двумя переменными одного из следующих видов:
y f(x); y ≥ f(x); y
Для изображения множества решений такого неравенства на координатной плоскости поступают следующим образом:
1. Строим график функции y = f(x), который разбивает плоскость на две области.
2. Выбираем любую из полученных областей и рассматриваем в ней произвольную точку. Проверяем выполнимость исходного неравенства для этой точки. Если в результате проверки получается верное числовое неравенство, то заключаем, что исходное неравенство выполняется во всей области, которой принадлежит выбранная точка. Таким образом, множеством решений неравенства – область, которой принадлежит выбранная точка. Если в результате проверки получается неверное числовое неравенство, то множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
3. Если неравенство строгое, то границы области, то есть точки графика функции y = f(x), не включают в множество решений и границу изображают пунктиром. Если неравенство нестрогое, то границы области, то есть точки графика функции y = f(x), включают в множество решений данного неравенства и границу в таком случае изображают сплошной линией.
А теперь рассмотрим несколько задач на эту тему.
Задача 1.
Какое множество точек задается неравенством x · y ≤ 4?
Решение.
1) Строим график уравнения x · y = 4. Для этого сначала преобразуем его. Очевидно, что x в данном случае не обращается в 0, так как иначе мы бы имели 0 · y = 4, что неверно. Значит, можем разделить наше уравнение на x. Получим: y = 4/x. Графиком данной функции является гипербола. Она разбивает всю плоскость на две области: ту, что между двумя ветвями гиперболы и ту, что снаружи их.
2) Выберем из первой области произвольную точку, пусть это будет точка (4; 2).
Проверяем неравенство: 4 · 2 ≤ 4 – неверно.
Значит, точки данной области не удовлетворяют исходному неравенству. Тогда можем сделать вывод о том, что множеством решений неравенства будет вторая область, которой выбранная точка не принадлежит.
3) Так как неравенство нестрогое, то граничные точки, то есть точки графика функции y = 4/x, рисуем сплошной линией.
Закрасим множество точек, которое задает исходное неравенство, желтым цветом (рис. 1).
Задача 2.
Изобразить область, заданную на координатной плоскости системой
{уx2 +2;
{y+x1;
{ x2 + y2 ≤ 9.
Решение.
Строим для начала графики следующих функций (рис. 2):
y = x2 + 2 – парабола,
y + x = 1 – прямая
x2 + y2 = 9 – окружность.

Теперь разбираемся с каждым неравенством в отдельности.
1) y x2 + 2.
Берем точку (0; 5), которая лежит выше графика функции.
Проверяем неравенство: 5 02 + 2 – верно.
Следовательно, все точки, лежащие выше данной параболы y = x2 + 2, удовлетворяют первому неравенству системы. Закрасим их желтым цветом.
2) y + x 1.
Берем точку (0; 3), которая лежит выше графика функции.
Проверяем неравенство: 3 + 0 1 – верно.
Следовательно, все точки, лежащие выше прямой y + x = 1, удовлетворяют второму неравенству системы. Закрасим их зеленой штриховкой.
3) x2 + y2 ≤ 9.
Берем точку (0; -4), которая лежит вне окружности x2 + y2 = 9.
Проверяем неравенство: 02 + (-4)2 ≤ 9 – неверно.
Следовательно, все точки, лежащие вне окружности x2 + y2 = 9,  не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
Не забываем о том, что если неравенство строгое, то соответствующую граничную линию следует рисовать пунктиром. Получаем следующую картинку (рис. 3).
Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис. 4).
Задача 3.
Изобразить область, заданную на координатной плоскости системой:
{x2 +y2 ≤16;
{x≥-y;
{x2 + y2 ≥ 4.
Решение.
Строим для начала графики следующих функций:
x2 + y2 = 16 – окружность,
x = -y – прямая
x2 + y2 = 4 – окружность (рис. 5).
Теперь разбираемся с каждым неравенством в отдельности.
1) x2 + y2 ≤ 16.
Берем точку (0; 0), которая лежит внутри окружности x2 + y2 = 16.
Проверяем неравенство: 02 + (0)2 ≤ 16 – верно.
Следовательно, все точки, лежащие внутри окружности x2 + y2 = 16, удовлетворяют первому неравенству системы.
Закрасим их красной штриховкой.
2) x ≥ -y.
Берем точку (1; 1), которая лежит выше графика функции.
Проверяем неравенство: 1 ≥ -1 – верно.
Следовательно, все точки, лежащие выше прямой x = -y, удовлетворяют второму неравенству системы. Закрасим их синей штриховкой.
3) x2 + y2 ≥ 4.
Берем точку (0; 5), которая лежит вне окружности x2 + y2 = 4.
Проверяем неравенство: 02 + 52 ≥ 4 – верно.
Следовательно, все точки, лежащие вне окружности x2 + y2 = 4, удовлетворяют третьему неравенству системы. Закрасим их голубым цветом.
В данной задаче все неравенства нестрогие, значит, все границы рисуем сплошной линией. Получаем следующую картинку (рис. 6).
Искомая область – это область, где все три раскрашенных области пересекаются друг с другом (рис 7).











 не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.
не удовлетворяют третьему неравенству системы. Тогда можем сделать вывод о том, что все точки, лежащие внутри окружности x2 + y2 = 9, удовлетворяют третьему неравенству системы. Закрасим их фиолетовой штриховкой.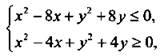 и вычислим площадь этой фигуры.
и вычислим площадь этой фигуры.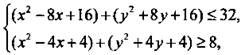 или
или 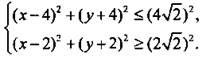

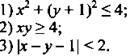
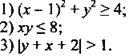
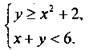
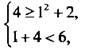 или
или 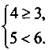
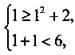 или
или 









