Решение задач с помощью кругов Эйлера.

Решение задач с помощью кругов Эйлера

Выполнила учитель математики

МАОУ «Школа № 4, г. Благовещенска»

Станишевская Т. В.

12

-20

15

-32

-26+(-6)=

Сложение отрицательных чисел

-70+50=

-136

17+(-30)=

Сложение положительных чисел

80+120=

Сложение

чисел с разными знаками

-63+(-73)=

200

-61+(+73)=

-13

136

120

88+(-73)=

A

A B = C

B

A

A B = D

B

A

B

A B =

Зачем нужны круги Эйлера?

Вставка рисунка

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера

Решение задач с помощью кругов Эйлера

Выводы: Круги  Эйлера – это геометрическая схема, которая позволяет делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Убедиться в этом можно на примере задачи.

Задача. Все мои подруги выращивают в своих квартирах какие-нибудь цветы. Шестеро из них разводят кактусы, а пятеро фиалки. И только у двух есть и кактусы и фиалки.  Сколько у меня подруг?

Решение задач с помощью кругов Эйлера

Задача 1 .

Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной или районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной. 

Р - районная библиотека 20

Ш – школьная библиотека 25

Всего – 35

Р

Ш

Сколько шестиклассников:

1. Являются читателями обеих библиотек; 2. Не являются читателями районной библиотеки; 3. Не являются читателями школьной библиотеки;  4. Являются читателями только районной библиотеки; 5. Являются читателями только школьной библиотеки?

Решение

Алгоритм решения задач

1.Внимательно изучаем и кратко записываем условие задачи.

2.Определяем количество множеств и обозначаем их.

3. Выполняем рисунок. Строим пересечение множеств.

4. Записываем исходные данные в круги.

5. Выбираем условие, в котором содержится больше свойств.

6. Записываем недостающие данные в круги Эйлера (рассуждая и анализируя)

Проверяем решение задачи  и записываем ответ

1. 20 + 25 – 35 = 10 (человек) – являются читателями обеих библиотек.

обе10

2. 35 – 25 = 10 (человек) – являются читателями только районной библиотеки.

Ш

Р

25

20

3. 35 – 20 = 15 (человек) – являются читателями только школьной библиотеки.

4. 35 – 20 = 15 (человек) – не являются

читателями районной библиотеки.

5. 35 – 25 = 10 (человек) – не являются читателями школьной библиотеки.

Всего 35

Задача №2:

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28 , французским – 42 . Английским и немецким одновременно владеют 8 человек, английским и французским - 10 , немецким и французским – 5 , всеми тремя языками – 3 .

Сколько туристов не владеют ни одним языком?

Решение :

Всего – 100

Н – немецкий (30)

А – английский (28)

Ф – французский (42)

Н

Ф

А

(Н и А) и часть Ф – 8

(Ф и А) и часть Н – 10

(Н и Ф) и часть А – 5

Все языки – 3

Не владеют ни одним языком?

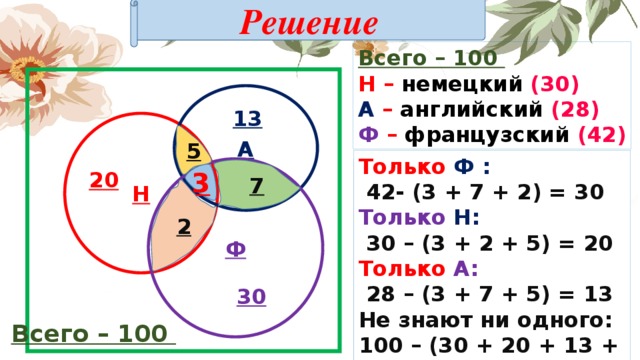
Решение

Всего – 100

Н – немецкий (30)

А – английский (28)

Ф – французский (42)

А

13

Н

5

Только Ф :

42- (3 + 7 + 2) = 30

Только Н:

30 – (3 + 2 + 5) = 20

Только А:

28 – (3 + 7 + 5) = 13

Не знают ни одного:

100 – (30 + 20 + 13 + 17) = 20

(Н и А) и часть Ф – 8,

Ф

8 – 3 = 5(только Н и А)

(Ф и А) и часть Н – 10,

10 – 3 = 7 (только Ф и А)

(Н и Ф) и часть А – 5,

5 – 3 = 2 (только Н и Ф)

Все - 3

7

20

3

2

30

Всего – 100

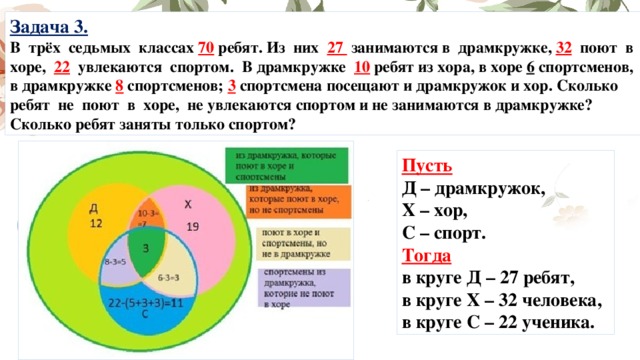
Задача 3.

В  трёх  седьмых  классах 70 ребят. Из  них  27  занимаются в  драмкружке,  32   поют  в хоре,  22   увлекаются  спортом.  В драмкружке  10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8  спортсменов; 3  спортсмена посещают и драмкружок и хор. Сколько  ребят  не  поют  в  хоре,  не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Пусть   Д – драмкружок,  Х – хор,  С – спорт.

Тогда   в круге Д – 27 ребят,  в круге Х – 32 человека,  в круге С – 22 ученика.

Д

Х

С

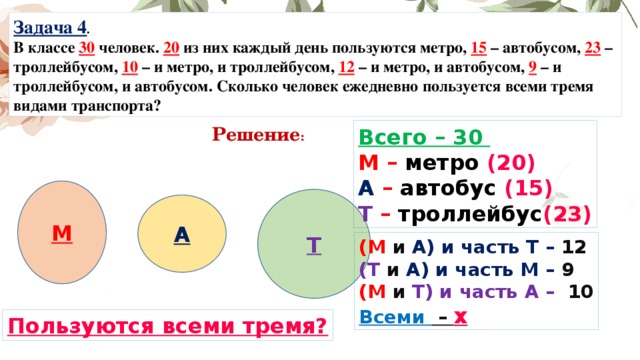
Задача 4 .

В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

Решение :

Всего – 30

М – метро (20)

А – автобус (15)

Т – троллейбус (23)

М

Т

А

(М и А) и часть Т – 12

(Т и А) и часть М – 9

(М и Т) и часть А – 10

Всеми – х

Пользуются всеми тремя?

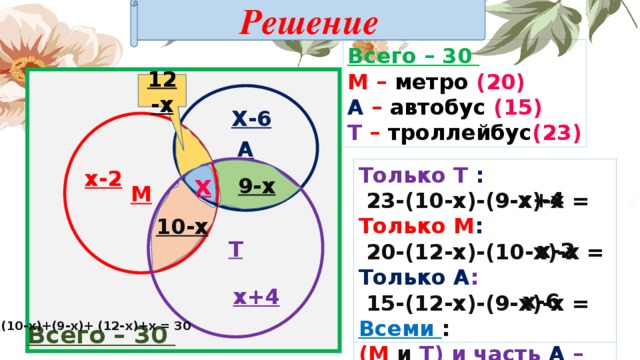
Решение

Всего – 30

М – метро (20)

А – автобус (15)

Т – троллейбус (23)

12-х

А

Х-6

М

Только Т :

Т

(М и А) и часть Т – 12,

23-(10-х)-(9-х)-х =

12 – х (только М и А )

(Т и А) и часть М – 9,

Только М :

20-(12-х)-(10-х)-х =

9 – х (только Т и А )

(М и Т) и часть А – 10,

Только А :

15-(12-х)-(9-х)-х =

10 – х (только М и Т )

Всеми – х

Всеми :

9-х

х-2

х

10-х

х+4

х-2

х+4

х-6

Всеми :

(х+4)+(х-2) +( х-6) + (10-х)+(9-х)+ (12-х)+х = 30

Всего – 30

Всеми :

(х+4)+(х-2) +( х-6) + (10-х)+(9-х)+ (12-х)+х = 30

х + 4 + х – 2 + х – 6 + 10 – х + 9 – х + 12 – х + х = 30

х + 27 = 30

х = 30 – 27

х = 3

Ответ: Пользуются всеми тремя видами транспорта

3 человека

Slide title

1

Click to add Title

2

Click to add Title

3

Click to add Title

4

Click to add Title

5

Click to add Title