___________класс, ___________сабак, ____________чейрек
Сабактын темасы: Ыктымалдыктын аныктамалары.
Сабактын максаты:
Билим берүүчүлүк:Ыктымалдыктар теориясынын аныктамаларын түшүнүшө. Комбинаториканын формулаларын билишет;
Өнүктүрүүчүлүк: Алган билимдерин жана формулалардын негизинде көнүгүүлөрдү аткарышат;
Тарбия берүүчүлүк:
Баалоо критерийи:
| “5” | “4” | “3” | “2” |
| Окуучу жаңы теманы толук түшүнүп ага анализ жүргүзө алса жана айткан маалыматтарды далилдей алса | Окуучу жаңы темага толук түшүнүп бирок анализдей жана далилдей албаса. Көп суроолорго жооп берүүдөн кыйналса | Окуучу теманы үстүрттөн түшунүп жөнөкөй суроолорго жооп бере алса. | Окуучу тема боюнча таптакыр түшүнүгү жок жана жөнөкөй суроолорго таптакыр жоооп бере албаса |
Сабактын тиби: Стандарттык
Сабактын формасы: Жекече, класстык
Сабактын жабдылышы: (доска, окуу китеби, проектор)
Сабактын жүрүшү: Уюштуруу (саламдашуу, балдарды толуктоо, маанай тартуулоо)
Үй тапшырасын текшерүү: Төмөндө келтирилген окуялардын кайсынысы а) кокустук, б) сөзсүз орундалуучу, в) сөзсүз орун албоочу болуша: 1) бир лотереялык билет боюнча утушка ээ болуу; 2) Жащиктеги 4 көк жана 6 кызыл шарлардын өндүү шарды сууруп алуу; 3) 200 беттүү китепти ачканда, 205-беттин ачылышы.
Жаңы тема: Ыктымалдыктар теориясы массалык мүнөздөгү кокус окуяларына ылайык келүү мыйзам ченемдүүлүктөрдү окуп-үйрөнүүгө багытталаган. Кокус окуясы так эсепке алуга мүмкүн болбогон көптөгөн себептердин таасиринин жыйынтыгы, ошондуктан ыктымалдыктар теориясы кандайдыр бир гана кокус окуянын ишке ашуусу же ишке ашпоосу жөнүндөгү суроого жооп бербейт. Ыйгайлуу болсун үчүн, мындан ары ар кандай окуяны А тамгасы менен белгилейли. Мисалы тыйындын герби жогору карап түштү А окуясы, ал эми номер жагынын түшүшү  окуясы. Эми n сыноодон турган тажрыйба жүргүзулүп, андагы А окуясынын m (
окуясы. Эми n сыноодон турган тажрыйба жүргүзулүп, андагы А окуясынын m ( жолу орун алышы карайлы. 1-аныктама: Кокус А окуясынын орун алган m санын сыноонун жалпы n саына болгон катышы анын жыштыгы д.а., б.а.
жолу орун алышы карайлы. 1-аныктама: Кокус А окуясынын орун алган m санын сыноонун жалпы n саына болгон катышы анын жыштыгы д.а., б.а.  бөлчөгү А окуясынын жыштыгы. Мындан
бөлчөгү А окуясынын жыштыгы. Мындан 
2-аныктама: Эгерде  бир тектүү кокус окуялары төмөнкү касиеттерге ээ болушса: 1. Ар кандай сыноодо алардан бир гана окуясы орун алса. 2. Бардыгы бирдей мүмкүнчүлүктөгү окуялар, анда аларды элементардык окуялар дешет.
бир тектүү кокус окуялары төмөнкү касиеттерге ээ болушса: 1. Ар кандай сыноодо алардан бир гана окуясы орун алса. 2. Бардыгы бирдей мүмкүнчүлүктөгү окуялар, анда аларды элементардык окуялар дешет.
3-аныктама: Эгерде А окуясы n элементардык окуялардын суммасынан турса, анда анын ыктымалдыгы төмөнкү санга барабар:  .
.
Мында, n-элементардык А окуясынын (сыноосунун) жалпы саны, ал эми А окуясынын орун алуусун камсыз кылган учурлардын саны жана  болгондуктан
болгондуктан  болот. Ошентип, сөзсүз орун албоочу окуянын ыктымалдыгы р=0 ал эми кокус окуянын ыктымалдыктары
болот. Ошентип, сөзсүз орун албоочу окуянын ыктымалдыгы р=0 ал эми кокус окуянын ыктымалдыктары  болору келип чыгат.
болору келип чыгат.
Мисалы: Куб түрүндөгү оюн сөөкчөсүнү ыргытсак, анда алты элементардык окуяга ээ болобуз: А1 – үстүңкү гранда 1 саны; А2 – 2 саны, А3 – 3, А4 – 4, А5 – 5, А6 – 6 саны. Үстүңкү жагында жуп сандуу гран түшкөн А окуясынын ыктымалдыктарын тапкыла. чыгаруу: Мисалдын шарты боюнча А=А2+А4+А6. Каалаганда А окуянын орун алышын А2, А4, А6 окуялары камсыз кыла алат, б.а. n=6 жана m=3. Анда жогорудагы аныктаманын негизинде 
4-аныктама: (статикалык) Эгерде салыштырма жыштык туруктуу болсо, анда аны  санын А окуясынын статикалык ыктымалдыгы дейбиз. мындагы, m – А окуясынын орун алганын саны, n – сыноонун жалпы саны.
санын А окуясынын статикалык ыктымалдыгы дейбиз. мындагы, m – А окуясынын орун алганын саны, n – сыноонун жалпы саны.




L
l
5-аныктама: (геометриялык) А окуясынын ыктымалдыгы төмөнкү формула менен табылат

,
Мисалы: Узундугу 10см болгон кесиндиге узундугу 2см болгон кичине кесинди жайгашылган. Болжол ыргытылган точка кичине кесиндиде жатуусун ыктымалдыгын эсептегиле. Чыгарылышы: Окуя А – ыргытылган точка кичине кесиндиде жатат. Анда ыктымалдыктын геометриялык аныктамасынын негизинде  . Ошентип, чексиз көп окуялардын ыктымалдыктары 0 менен 1 сандарынын арасында жаткан чексиз көп чыныгы сандар сенен мүнөздөлөт экен
. Ошентип, чексиз көп окуялардын ыктымалдыктары 0 менен 1 сандарынын арасында жаткан чексиз көп чыныгы сандар сенен мүнөздөлөт экен  . Эгерде ыктымалдык эң кичине сан болсо (0гө жакын) анда ал окуянын ишке ашуу мүмкүнчүлүгү өтө аз, ал эми ыктымалдык 1ге жакын болсо, анда ал окуянын ишке ашуу мүмкүнчүлүгү чоң (жогору) болот.
. Эгерде ыктымалдык эң кичине сан болсо (0гө жакын) анда ал окуянын ишке ашуу мүмкүнчүлүгү өтө аз, ал эми ыктымалдык 1ге жакын болсо, анда ал окуянын ишке ашуу мүмкүнчүлүгү чоң (жогору) болот.
Комбинаториканын формулалары
Кокус окуялардын ыктымалдыктарын түздөн-түз эсептөөдө комбинаториканын формулаларын көп колдонулат, ошондуктан аларга токтолоу.
6-аныктама: Ар кандай n элементтерди m ден орундаштыруу деп, курамы жана ирээти менен айырмаланган биргелешүүнүн түрүн айтабыз. Ар кандай n элементтерден m орундаштыруунун санын  менен белгилесек, анда ал сан төмөнкү формла менен эсепетелинет:
менен белгилесек, анда ал сан төмөнкү формла менен эсепетелинет:

Мисалы: 1; 2; 3 сандарын (элементтерин) эки сандан (элементтен) төмөнкүчө орундаштыра алабыз: 12, 13, 21, 31, 23, 32, б.а. бардыгы ар кандай алты орундаштыруу (курамы, ирээти ар түрдүү)

7-анкытама: Ар кандай n элементтердин орун алмаштыруусу деп, алардын n ден бардык мүмкүн болгон орундаштыруусун айтабыз. Ар кандай n элементтердин орун алмашуусун  деп белгилесе, анда алардын саны төмөнкүчө табылат:
деп белгилесе, анда алардын саны төмөнкүчө табылат: 
Мисалы: 1; 2; 3 сандарынын ороун алмаштыруусу алардын 3 төн болгон орундаштыруусу: 123, 213, 231, 312, 321, 132.
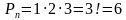
8-аныктама: Ар кандай n элементтерди m ден топтоштуруу деп, бири-биринен курамы боюнча гана айырмаланган биргелешүүнүн түрүн айтабыз жана аны  менен белгилейбиз. Анда топтоштуруунун саны:
менен белгилейбиз. Анда топтоштуруунун саны:
Мисалы: Дүн соода дүкөнүндөгу 10 компьютердин 7си жарактуу. Капысынан сатып алынган 6 компьютердин 4ү жарактуу болоорунун ыктымалдыгын тапкыла.
Чыгаруу: Сатып алынган 6 компьютердин 4өө жарактуу болушун А окуясы десек, анда элементардык сыноонун жалпы саны 10 элементти 6дан топтоштуруунун санына барабар.
Ал эми А окуясына ылайык келүүчү жыйынтыктардын саны: 7 жалпы жарактууну 4 жарактуудан топтоштуруулуардын саны б.а. ти жараксыздыгынын жалпы 10 – 7 =3 санын, капысынан сатып алган 6 – 4=2 ден топтоштурганга б.а. кө көбөйткөнгө барабар, демек; m = Ошентип,
Ошентип,
Бышыктоо: 1-көнүгүү: Баштыкта бирдей формадагы 12 шар бар, анын 5и кара жана 7си ак болсо, кара шарды сууруп чыгуунун ыктымалдыгын тапкыла.

2-көнүгүү: Бүтүн 1ден 60ка чейинки сандар берилсе, анда капысынан алыган бүтүн сан 60 санынын бөлүүчүсү болоорун ыктымалдыгы канчага барабар?
60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30. – 11 бөлүүчүсү бар демек 
3 -көнүгүү: 1ден 30га чейинки номерленген экзамендик билеттердин бирөөсү капысынан алынса, анда ал билеттин номеринин 3 санына эселүү болушунун ыктымалдыгын эсептегиле.
Чыгаруу: маселенин шарты боюнча, сынообуз бир билетти капсы алуу болот. Ал эми А окуясы алынган билеттин номери 3 санына эселүү болушу. Демек, сыноонун жалпы саны 30 жана А окуясынын орун алуусуна ылайык келүүчүлөрү: 3; 6; 9; 12; 15; 18; 21; 24; 27; 30 билеттери б.а. m=10. Формула боюнча  ;
;
Жыйынтыктоо:Ыктымалдыктын классикалык, статистикалык жана геометриялык аныктамаларын кайталап айтып берүү.
Үй тапшырма: Акча – буюм лотереясындагы 1000 билетке 120 буюм жана 50 акча утушу бар болсо, бир лотереялык билети бар адамдын утуу ыктымалдыгын тапкыла.
120+50=170 жалпы отуштун саны,






 окуясы. Эми n сыноодон турган тажрыйба жүргүзулүп, андагы А окуясынын m (
окуясы. Эми n сыноодон турган тажрыйба жүргүзулүп, андагы А окуясынын m ( жолу орун алышы карайлы. 1-аныктама: Кокус А окуясынын орун алган m санын сыноонун жалпы n саына болгон катышы анын жыштыгы д.а., б.а.
жолу орун алышы карайлы. 1-аныктама: Кокус А окуясынын орун алган m санын сыноонун жалпы n саына болгон катышы анын жыштыгы д.а., б.а.  бөлчөгү А окуясынын жыштыгы. Мындан
бөлчөгү А окуясынын жыштыгы. Мындан 
 бир тектүү кокус окуялары төмөнкү касиеттерге ээ болушса: 1. Ар кандай сыноодо алардан бир гана окуясы орун алса. 2. Бардыгы бирдей мүмкүнчүлүктөгү окуялар, анда аларды элементардык окуялар дешет.
бир тектүү кокус окуялары төмөнкү касиеттерге ээ болушса: 1. Ар кандай сыноодо алардан бир гана окуясы орун алса. 2. Бардыгы бирдей мүмкүнчүлүктөгү окуялар, анда аларды элементардык окуялар дешет. .
. болгондуктан
болгондуктан  болот. Ошентип, сөзсүз орун албоочу окуянын ыктымалдыгы р=0 ал эми кокус окуянын ыктымалдыктары
болот. Ошентип, сөзсүз орун албоочу окуянын ыктымалдыгы р=0 ал эми кокус окуянын ыктымалдыктары  болору келип чыгат.
болору келип чыгат.
 санын А окуясынын статикалык ыктымалдыгы дейбиз. мындагы, m – А окуясынын орун алганын саны, n – сыноонун жалпы саны.
санын А окуясынын статикалык ыктымалдыгы дейбиз. мындагы, m – А окуясынын орун алганын саны, n – сыноонун жалпы саны.



 ,
,  . Ошентип, чексиз көп окуялардын ыктымалдыктары 0 менен 1 сандарынын арасында жаткан чексиз көп чыныгы сандар сенен мүнөздөлөт экен
. Ошентип, чексиз көп окуялардын ыктымалдыктары 0 менен 1 сандарынын арасында жаткан чексиз көп чыныгы сандар сенен мүнөздөлөт экен  . Эгерде ыктымалдык эң кичине сан болсо (0гө жакын) анда ал окуянын ишке ашуу мүмкүнчүлүгү өтө аз, ал эми ыктымалдык 1ге жакын болсо, анда ал окуянын ишке ашуу мүмкүнчүлүгү чоң (жогору) болот.
. Эгерде ыктымалдык эң кичине сан болсо (0гө жакын) анда ал окуянын ишке ашуу мүмкүнчүлүгү өтө аз, ал эми ыктымалдык 1ге жакын болсо, анда ал окуянын ишке ашуу мүмкүнчүлүгү чоң (жогору) болот. менен белгилесек, анда ал сан төмөнкү формла менен эсепетелинет:
менен белгилесек, анда ал сан төмөнкү формла менен эсепетелинет:

 деп белгилесе, анда алардын саны төмөнкүчө табылат:
деп белгилесе, анда алардын саны төмөнкүчө табылат: 
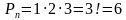
 менен белгилейбиз. Анда топтоштуруунун саны:
менен белгилейбиз. Анда топтоштуруунун саны:









