РЕШУ ВПР — математика–7
Вариант № 3152728
1.
Найдите значение выражения 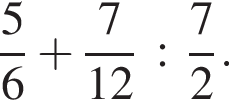
ИЛИ
Найдите значение выражения 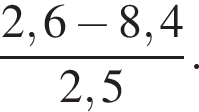
Решение. Вычислим:
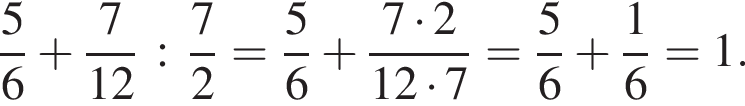
Ответ: 1.
ИЛИ
Сократим:

Ответ: −2,32.
2. Определите явно ошибочное значение (выброс), внесённое в эту таблицу.
ИЛИ
Определите, в каком из этих регионов наибольшая численность населения.
Решение. Выбросом являются данные о росте Евсеевой — 1154 см.
Ответ: 1154.
ИЛИ
Из диаграммы видим, что наибольшая численность населения в Республике Дагестан.
Ответ: Республика Дагестан.
3. Удалите выброс и найдите размах оставшихся значений.
ИЛИ
Найдите примерную долю населения Чеченской Республики в общей численности населения СКФО. Ответ дайте в процентах.
Решение. Выбросом являются данные о росте Евсеевой — 1154 см. Найдем размах оставшихся значений. Максимальное значение выборки — 167 см, минимальное — 149 см, следовательно, размах значений выборки равен 167 − 149 = 18.
Ответ: 18.
ИЛИ
Из диаграммы видим, что население Чеченской Республики составляет чуть больше  части от общей численности населения СКФО, то есть 12,5%.
части от общей численности населения СКФО, то есть 12,5%.
Ответ: от 12 до 20%.
4. Трактор едет по дороге, проезжая 10 метров за каждую секунду. Выразите скорость трактора в километрах в час. В ответе укажите число.
Решение. Трактор двигается со скоростью 10 м/с. Выразим эту скорость в километрах в час: 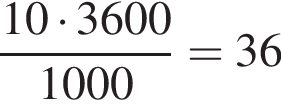 км/ч.
км/ч.
Ответ: 36.
5. Катя младше Тани, но старше Даши. Ксюша не младше Даши. Укажите номера истинных утверждений.
1) Таня и Даша одного возраста.
2) Среди указанных девочек нет никого младше Даши.
3) Таня старше Даши.
4) Таня и Катя одного возраста.
Решение. 1) Неверно, так как Таня старше Кати, а Катя старше Даши.
2) Верно. 3) Верно, так как Таня старше Кати, а Катя старше Даши.
4) Неверно, так как Катя младше Тани.
Ответ: 23.
6. Найдите корень уравнения 
Решение. Последовательно получаем:
Ответ: −3.
7.
Отметьте на числовой прямой точку 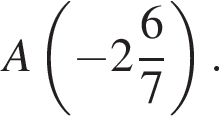
Решение. Отметим точку A на числовой прямой (см. рис.).
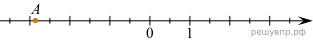
8.
 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC. В ответе укажите число.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC. В ответе укажите число.
Решение. Расстояние от точки до прямой равно длине перпендикуляра, опущенного из этой точки на прямую. По рисунку определяем это расстояние, оно равно двум клеткам, или 2 см.
Ответ: 2.
9.
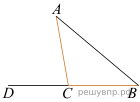 В треугольнике ABC угол BAC равен 40°, АC = CB. Найдите внешний угол при вершине C.
В треугольнике ABC угол BAC равен 40°, АC = CB. Найдите внешний угол при вершине C.
Решение. Так как АC = CB, треугольник ABC — равнобедренный, следовательно, углы BAC и ABC равны 40°. Отсюда угол ACB равен 180° − 40° · 2 = 100°. По свойству смежных углов, внешний угол при вершине C равен 80°.
Ответ: 80.
10.
Из пункта А в направлении пункта Б, расстояние между которыми равно 240 км, в 7 часов утра выехал велосипедист, а через некоторое время из пункта А в том же направлении выехал автомобиль. Доехав до пункта Б, автомобиль сделал остановку на 3 часа, а затем с той же скоростью поехал обратно.
На рисунке график движения велосипедиста обозначен цифрой 1, график движения автомобиля обозначен цифрой 2 и приведён не полностью.
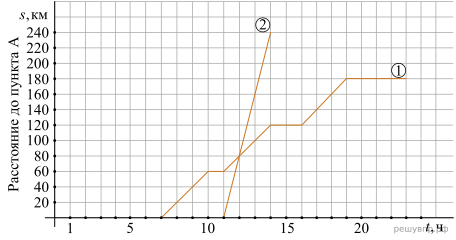
Найдите, на каком расстоянии от пункта А автомобиль догнал велосипедиста.
Решение. Из графика видим, что автомобиль догнал велосипедиста на расстоянии 80 км от пункта А.
Ответ: 80.
11. На том же рисунке достройте график движения автомобиля до момента возвращения в пункт А.
Решение. Достроим график движения автомобиля до момента возвращения в пункт А.
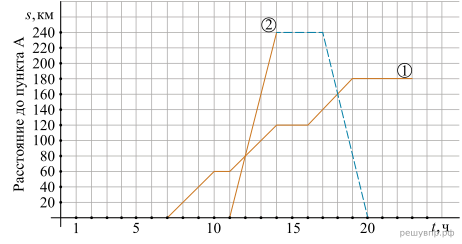
Ответ: см. рис.
12.
Найдите значение выражения  при
при 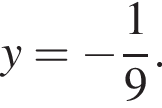
Решение. Упростим выражение:
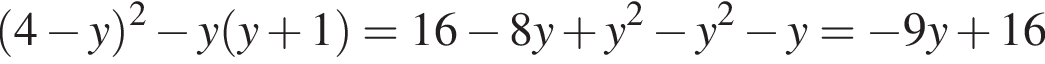
Найдём значение полученного выражения при 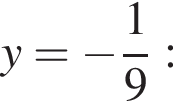
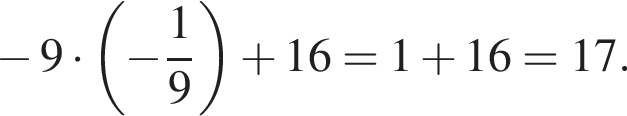
Ответ: 17.
13.
 На рисунке показан абажур, изготовленный из стальной проволоки. Какое наименьшее количество кусков проволоки нужно, чтобы изготовить абажур, показанный на рисунке?
На рисунке показан абажур, изготовленный из стальной проволоки. Какое наименьшее количество кусков проволоки нужно, чтобы изготовить абажур, показанный на рисунке?
Решение. 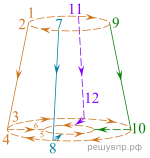 Абажур можно рассмотреть как граф с 12-ю вершинами, из которых 8 — нечетной степени. Если проволока проходит через вершину, то она объединяет два ребра, сходящиеся в этой вершине, поэтому в каждой вершине нечетной степени хотя бы одна проволока должна начинаться или заканчиваться. Вершин нечетной степени 8, а у каждой проволоки два конца, следовательно, потребуется не менее четырех кусков проволоки.
Абажур можно рассмотреть как граф с 12-ю вершинами, из которых 8 — нечетной степени. Если проволока проходит через вершину, то она объединяет два ребра, сходящиеся в этой вершине, поэтому в каждой вершине нечетной степени хотя бы одна проволока должна начинаться или заканчиваться. Вершин нечетной степени 8, а у каждой проволоки два конца, следовательно, потребуется не менее четырех кусков проволоки.
Как сделать абажур из четырех кусков, показано на рисунке: выйдем из одной нечетной вершины (вершина 1 на рисунке, путь указан оранжевыми стрелками), закончим обход в другой нечетной вершине (вершина 6), а в каждую из вершин четного индекса зайдем и выйдем необходимое число раз. Оставшиеся вершины 7 и 8, 9 и 10, 11 и 12 соединим еще тремя кусками проволоки.
Ответ: 4.
14.
Решите систему уравнений
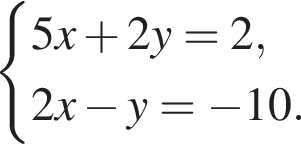
Решение. Последовательно получаем:
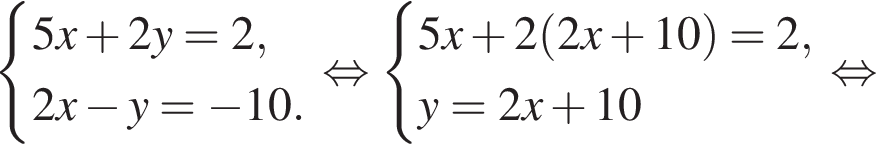
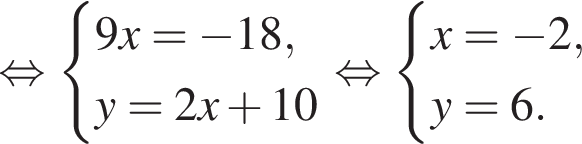
Ответ: 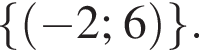
15. Хоккейные коньки в апреле стоили 4500 руб. В мае цену снизили на 20%. В октябре цену повысили на 10%. Сколько стали стоить коньки?
Решение. После снижения цены коньки стали стоить
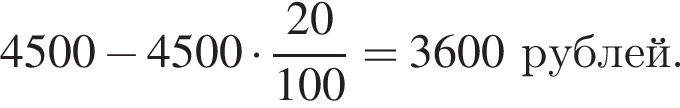
После повышения цены коньки стали стоить:

Ответ: 3960 рублей.
16.
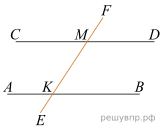 Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28°. Найдите угол AKM.
Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28°. Найдите угол AKM.
Решение. Сумма углов AKM и KMC равна 180°, углы FMD и KMC равны, тогда угол AKM равен 
Ответ: 152°.
17. На первом участке собрали по 420 тонн огурцов с каждого гектара; на втором — по 360 тонн, а на третьем — по 520 тонн. Площадь первого участка равна 20; второго — 55; третьего — 25 гектаров. Сколько тонн огурцов собрали в среднем с одного гектара на всех трех участках?
Решение. Со всех трех участков собрали:  тонн огурцов. Общая площадь трёх участков:
тонн огурцов. Общая площадь трёх участков: 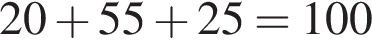 гектаров. Средняя урожайность:
гектаров. Средняя урожайность: 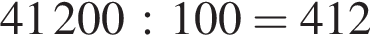 тонн огурцов с гектара.
тонн огурцов с гектара.
Ответ: 412 тонн.
18. В треугольнике ABC проведена биссектриса CE. Найдите величину угла BCE, если ∠BAC = 46° и ∠ABC = 78°.
ИЛИ
В треугольнике АВС на стороне АС отметили произвольную точку М. В треугольнике ABM провели биссектрису MK. В треугольнике СВМ построили высоту МР. Угол KMP равен 90°, CM = 12. Найдите ВM.
Решение. 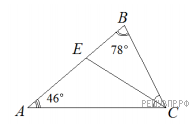 Сначала найдём угол ACB:
Сначала найдём угол ACB:
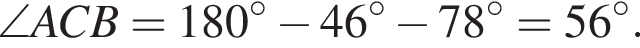
Поскольку CE биссектриса, 
Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.
Ответ: 28°.
ИЛИ
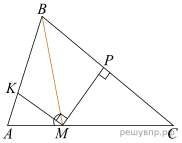
Пусть  тогда
тогда

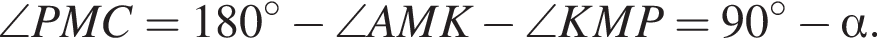
Получаем  Треугольники BMP и CMP равны. Значит, BM = CM = 12.
Треугольники BMP и CMP равны. Значит, BM = CM = 12.
Ответ: 12.
19. Задумали трёхзначное число, последняя цифра которого не равна нулю. Из него вычли трёхзначное число, записанное теми же цифрами в обратном порядке. Получили число 792. Найдите все числа, обладающие таким свойством.
Решение. Пусть задано число 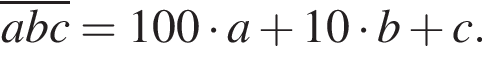 Из него вычли число
Из него вычли число 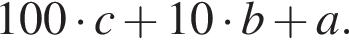 Имеем:
Имеем:
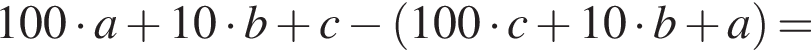
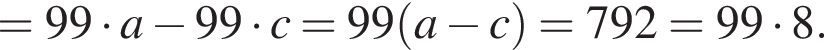
Следовательно,  Поскольку
Поскольку  и
и 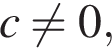 получаем
получаем  и
и  Значит, было задано одно из чисел: 901, 911, 921, 931, 941, 951, 961, 971, 981 или 991.
Значит, было задано одно из чисел: 901, 911, 921, 931, 941, 951, 961, 971, 981 или 991.
Ответ: 901, 911, 921, 931, 941, 951, 961, 971, 981 или 991.







 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC. В ответе укажите число.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC. В ответе укажите число. В треугольнике ABC угол BAC равен 40°, АC = CB. Найдите внешний угол при вершине C.
В треугольнике ABC угол BAC равен 40°, АC = CB. Найдите внешний угол при вершине C.

 На рисунке показан абажур, изготовленный из стальной проволоки. Какое наименьшее количество кусков проволоки нужно, чтобы изготовить абажур, показанный на рисунке?
На рисунке показан абажур, изготовленный из стальной проволоки. Какое наименьшее количество кусков проволоки нужно, чтобы изготовить абажур, показанный на рисунке? Абажур можно рассмотреть как граф с 12-ю вершинами, из которых 8 — нечетной степени. Если проволока проходит через вершину, то она объединяет два ребра, сходящиеся в этой вершине, поэтому в каждой вершине нечетной степени хотя бы одна проволока должна начинаться или заканчиваться. Вершин нечетной степени 8, а у каждой проволоки два конца, следовательно, потребуется не менее четырех кусков проволоки.
Абажур можно рассмотреть как граф с 12-ю вершинами, из которых 8 — нечетной степени. Если проволока проходит через вершину, то она объединяет два ребра, сходящиеся в этой вершине, поэтому в каждой вершине нечетной степени хотя бы одна проволока должна начинаться или заканчиваться. Вершин нечетной степени 8, а у каждой проволоки два конца, следовательно, потребуется не менее четырех кусков проволоки.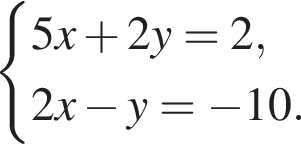
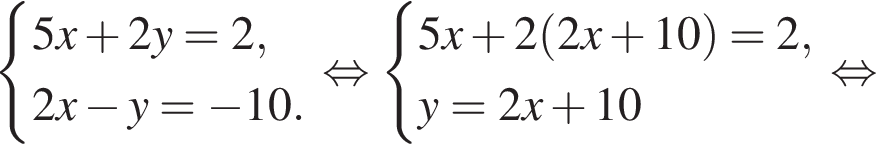
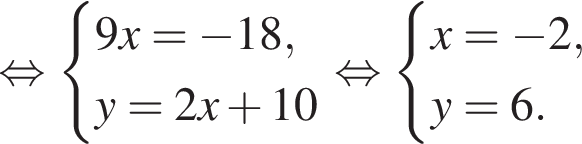
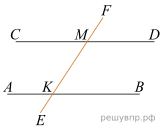 Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28°. Найдите угол AKM.
Параллельные прямые AB и CD пересекают прямую EF в точках K и M соответственно. Угол FMD равен 28°. Найдите угол AKM. Сначала найдём угол ACB:
Сначала найдём угол ACB:




















