МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ САМОСТОЯТЕЛЬНОЙ РАБОТЫ № 2
ТЕМА «Производная функции»
»
Цель: закрепить правила вычисления производных, отработать навыки и умения вычислять производные, развивать умение логически мыслить, формировать умение самоконтроля.
Для выполнения самостоятельной работы обучающийся должен знать определение производной, таблицу производных, правила дифференцирования, правило вычисления производной сложной функции.
Производная и первообразная функции, ее геометрический и физический смысл.
Пусть на некотором промежутке 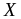 определена некоторая функция
определена некоторая функция 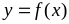
Вычисление производной функции 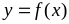 производится по общему правилу дифференцирования:
производится по общему правилу дифференцирования:
Придавая аргументу  приращение
приращение  и подставляя в выражение функции вместо аргумента
и подставляя в выражение функции вместо аргумента  наращенное значение
наращенное значение  +
+ , находим наращенное значение функции:
, находим наращенное значение функции:

Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции:
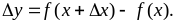
Делим приращение функции  на приращение аргумента
на приращение аргумента  , т.е. составляем отношение:
, т.е. составляем отношение:
 .
.
Находим предел этого отношения при 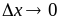 :
:
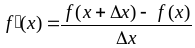 .
.
Этот предел и есть производная от функции 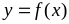 . Итак:
. Итак:
Производной функции f(x) в точке х=х0 называется отношение приращения функции 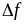 в этой точке к приращению
в этой точке к приращению  аргумента, при стремлении последнего к нулю.
аргумента, при стремлении последнего к нулю.
 .
.
Нахождение производной называется дифференцированием.
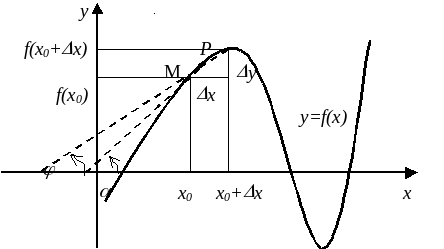
Пусть f(x) определена на некотором промежутке (a, b). Тогда 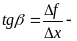 тангенс угла наклона секущей МР к графику функции (рис.10).
тангенс угла наклона секущей МР к графику функции (рис.10).
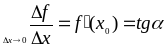 ,
,
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
Уравнение касательной к кривой: 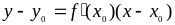
Уравнение нормали к кривой: 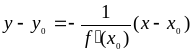 .
.
Фактически производная функции показывает скорость изменения функции, т.е. как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) Производная суммы (разности): (u ± v)¢ = u¢ ± v¢
2) Производная произведения: (u×v)¢ = u×v¢ + u¢×v
3) Производная частного: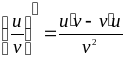 , если v ¹ 0
, если v ¹ 0
4) Производная сложной функции:
Первообразная функция.
Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают:
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
, где u, v, w – некоторые функции от х.
Таблица производных и первообразных некоторых основных элементарных функций.
| № | Первообразная  | Функция  | Производная  |
| 1. | 
| 
| 
|
| 2. | | 
| 
|
| 3. | 
| 
| 
|
| 4. | 
| 
| 
|
| 5. | 
| 
| 
|
| 6. | 
| 
| 
|
| 7. | 
| 
| 
|
| 8. | | 
| 
|
| 9. | 
| 
| 
|
| 10. | 
| 
| 
|
| 11. | | 
| 
|
| 12. | 
| 
| 
|
| 13. | | | |
Определенный интеграл.
Определенным интегралом функции f(x) от a до b называют разность значений первообразной этой функции в точках a и b.
Формула Ньютона-Лейбница:
.
Площадь криволинейной трапеции, ограниченной осью 0X, прямыми  и
и  и графиком неотрицательной функции
и графиком неотрицательной функции  на отрезке
на отрезке  находится по формуле:
находится по формуле:
 .
.
Задания для самостоятельной работы
Вариант 1
1.Для функции y = x2 найдите приращение ∆y, если x0=1 ,∆x=0,6.
2.Найдите производную функции: а) f(x) =  x3+x2+2x; б) g(x) =
x3+x2+2x; б) g(x) = 
в) g(x) = 4sinx- и вычислите g′
г) h(x) =  и вычислите h′ (-1).
и вычислите h′ (-1).
3.Решите уравнение если f(x) =
4.Необязательное задание. Имеет ли производную функция f(x) = -0,5x|x| в точке x=0?
Вариант 2
1.Для функции y = 0,5x2 найдите приращение ∆y, если x0=1 ,∆x=0,8.
2. Найдите производную функции: а) f(x) = -  x3+2x2-x; б) g(x) =
x3+2x2-x; б) g(x) =  +x;
+x;
в)g(x) = 3cosx и вычислите g′

г)h(x) =  и вычислите h′ (1).
и вычислите h′ (1).
3.Решите уравнение если f(x) =
 - 18x, g(x) =2
- 18x, g(x) =2 .
.
4.Необязательное задание. Имеет ли производную функция f(x) =2x|x| в точке x=0?
Вариант 3
1.Найдите угловой коэффициент секущей к графику функции y = x , проходящей через точки графика с абсциссами x0=0,5, х0+∆х=2.
, проходящей через точки графика с абсциссами x0=0,5, х0+∆х=2.
2.Найдите производную функции: а) f(x) =  б) g(x) =
б) g(x) = 
в) g(x) = 2tg x и вычислите g′ ; г) h(x) =
; г) h(x) =  и вычислите h′ ( - 2).
и вычислите h′ ( - 2).
3.Решите уравнение f′ (x)g′ (x) = 0, если f(x) = x3 – 6x2 , g(x)=
, g(x)=  .
.
4.Необязательное задание. Дана функция f(x) = x +1, где x≥0. Найдите функцию g(x) такую, чтобы выполнялось условие f(g(x)) = x.
Вариант 4
Найдите угловой коэффициент секущей к графику функции y = 0,5x , проходящей через точки графика с абсциссами x0=0,6 и x0+∆x=2.
Найдите производную функции:
а)f(x)=-
б) g(x) = 
в) g(x) = 4ctgx — и вычислите g′=

г) h(x) = (3x+4)/(x-3) — и вычислите h′ (4).
3.Решите уравнение f′ (x)g′ (x) = 0, если f(x) = x3-3x2, g(x) = 
4.Необязательное задание. Дана функция f(x) = x2 - 2,где x≥0.Найдите функцию g(x) такую, чтобы выполнялось условие g(f(x)) = x.
Тест по теме «Производная»
Вариант 1
Часть А.
А 1. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 2. Приведя функцию  к виду
к виду  , найдите производную
, найдите производную
1)  2)
2)  3)
3)  4)
4) 

А 3.  Решите уравнение
Решите уравнение 
1) 0 2) 4 3) 0; −4 4) 0; 4
А 4. Используя формулу производной суммы, найдите производную функции
1)  2)
2)  3)
3)  4)
4) 
А 5. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 6. Найдите значение производной функции  в точке
в точке 
1) 0 2) 1 3) −1 4) не существует
А 7. Найдите производную произведения функций  и
и 
1)  2)
2) 
3)  4)
4) 
А 8. Используя формулу производной частного, найдите производную функции
1)  2) 5 3)
2) 5 3)  4)
4) 
А 9. Найдите производную функции 
1) 0 2)  3)
3)  4)
4) 
А 10. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
Часть В.
В 1. Найдите 
В 2. Найдите производную функции  в точке
в точке 
Вариант 2
Часть А.
А 1. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 2. Приведя функцию  к виду
к виду  , найдите производную.
, найдите производную.
1)  2)
2)  3)
3)  4)
4) 
А 3.  Решите уравнение
Решите уравнение 
1) 0 2) 2 3) 0; 2 4) 0; −2
А 4. Используя формулу производной суммы, найдите производную функции
1)  2)
2)  3)
3)  4)
4) 
А 5. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 6. Найдите значение производной функции  в точке
в точке 
1)  2)
2)  3)
3)  4) 4
4) 4
А 7. Найдите производную произведения функций  и
и 
1)  2)
2)  3)
3)  4)
4) 
А 8. Найдите производную дробно- рациональной функции
1)  2)
2)  3)
3)  4)
4) 
А 9. . Найдите производную функции
1)  2) 3) 4)
2) 3) 4) 
А 10. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
Часть В.
В 1. Найдите 
В 2. Найдите производную функции  в точке
в точке 
Вариант 3
Часть А.
А 1. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 2. Приведя функцию  к виду
к виду  , найдите производную.
, найдите производную.
1)  2)
2)  3)
3)  4)
4) 
А 3.  Решите уравнение
Решите уравнение 
1) 0 2) 0; 3 3) 3 4) 0; −3
А 4. Используя формулу производной суммы, найдите производную функции
1)  2)
2)  3)
3)  4)
4) 
А 5. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 6. Найдите значение производной функции  в точке
в точке 
1) 1 2)  3)
3)  4) 2
4) 2
А 7. Найдите производную произведения функций  и
и 
1)  2)
2)  3)
3)  4)
4)
А 8. Найдите производную дробно- рациональной функции
1)  2)
2)  3)
3) 4)
4) 
А 9. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
А 10. Найдите производную функции 
1)  2)
2)  3)
3)  4)
4) 
Часть В
В 1. Найдите 
В 2. Найдите производную функции  в точке
в точке 
Рекомендации по оценке результатов тестирования:
| Количество верно выполненных заданий | 11−12 | 9 − 10 | 7 − 8 | 0 − 6
|
| Отметка | 5 | 4 | 3 | 2 |
Ключи к тесту по теме «Производная»
Вариант 1
| Номер задания | А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | А 7 | А 8 | А 9 | А 10 | В 1 | В 2 |
| Ответ | 4 | 4 | 4 | 1 | 2 | 2 | 1 | 1 | 2 | 3 | 0 | 1 |
 Вариант 2
Вариант 2
| Номер задания | А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | А 7 | А 8 | А 9 | А 10 | В 1 | В 2 |
| Ответ | 3 | 3 | 3 | 2 | 1 | 4 | 4 | 3 | 3 | 1 | 5 | 2 |
Вариант 3
| Номер задания | А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | А 7 | А 8 | А 9 | А 10 | В 1 | В 2 |
| Ответ | 2 | 3 | 2 | 1 | 1 | 4 | 4 | 3 | 4 | 2 | 3 | 0 |
МАОУ «СОШ № 57 г. Улан-Удэ имени А. Цыденжапова» Страница 11








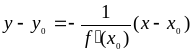 .
.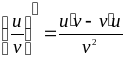 , если v ¹ 0
, если v ¹ 0 









