СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ
Сетевое планирование и управление (СПУ) – система методов планирования и управления разработкой больших и сложных объектов, для создания которых необходимо выполнить целый комплекс работ. СПУ основано на моделировании процесса с помощью сетевого графика.
Впервые СПУ было использовано в США в конце 50-х годов ХХ века для управления строительными работами, а также при разработке систем «Поларис». В России работы по сетевому планированию начались в 60-х годах.
Система СПУ позволяет: определить продолжительность проведения всего комплекса работ; формировать календарный план реализации комплекса работ; выявлять резервы времени; мобилизовывать трудовые, материальные и денежные ресурсы; повышать эффективность управления.
Основными понятиями СПУ являются работа и событие.
Под работой понимаются любые действия, трудовые процессы, сопровождающиеся затратами ресурсов или времени, и приводящие к определённым результатам.
 Под событием понимают результат завершения одной или нескольких работ. При этом предполагается, что событие не имеет продолжительности, оно констатирует факт выполнения одной или нескольких работ (рис. 1).
Под событием понимают результат завершения одной или нескольких работ. При этом предполагается, что событие не имеет продолжительности, оно констатирует факт выполнения одной или нескольких работ (рис. 1).
Работы на сети изображают направленными отрезками прямых произвольной длины, а события – обычно кружками, в которых указывают порядковый номер или шифр события. У каждой стрелки проставляется время выполнения работы или другие числовые характеристики (расход ресурса, количество исполнителей и т.д.).
Прежде чем строить сетевой график, надо составить подробный список работ, в отношении каждой работы выяснить её технологические связи с другими работами, конечные результаты (события) каждой работы, оценить длительность каждой работы.
| Пример 1. Список работ по организации выступления хора при свечах. | Таблица 1 |
| Работа (обозначение) | Описание работы | Непосредственно предшествующие работы | Продолжительность работы (в днях) |
| A | Выбор музыкального произведения | | 2 |
| B | Разучивание музыки | A | 14 |
| C | Размножение нот | A | 14 |
| D | Пробные спевки | B, C | 3 |
| E | Репетиции хора | D | 7 |
| F | Репетиции солистов | D | 7 |
| G | Получение канделябров в прокат | D | 1 |
| H | Закупка свечей | G | 1 |
| I | Установка канделябров | H | 1 |
| J | Закупка декораций | D | 1 |
| K | Установка декораций | J | 1 |
| L | Заказ костюмов для хора | D | 7 |
| M | Отглаживание костюмов | L | 7 |
| N | Проверка системы усиления звука | D | 7 |
| O | Генеральная репетиция | K, E, F, N | 1 |
| P | Проведение концерта | M, O, I | 1 |
|
|
|
|
|
Построение сетевой модели
После того как подготовительный этап будет закончен (составлен перечень работ), приступают к построению сетевой модели.
При этом необходимо соблюдать ряд правил.
1
 . Если работы А, В и С выполняются последовательно, то они изображаются следующим образом.
. Если работы А, В и С выполняются последовательно, то они изображаются следующим образом.
2. Если для выполнения работ В и С необходим результат работы А, то они изображаются следующим образом.

3 . Если для выполнения работы С необходимы результаты работ А и В, то это изображается следующим образом.
. Если для выполнения работы С необходимы результаты работ А и В, то это изображается следующим образом.
4. Если работы А, В и С начинаются и заканчиваются одними и теми же событиями (т.е. эти работы можно выполнять одновременно), то вводятся фиктивные работы.
5. В сети не должно быть событий, в которые не входит ни одна работа, кроме начального.
6 . В сети не должно быть ни одного события, из которого не выходит ни одной работы, кроме завершающего.
. В сети не должно быть ни одного события, из которого не выходит ни одной работы, кроме завершающего.
7. В сети не должно быть замкнутого контура.
8. События следует нумеровать так, чтобы номер исходного события данной работы был меньше номера завершающего события.
|
| Таблица 2 |
|
| Работа (обозначение) | Непосредственно предшествующие работы | Продолжительность работы |
| A | | 3 |
| B | | 6 |
| C | | 4 |
| D | A | 5 |
| E | A, B | 1 |
| F | A, B | 9 |
| G | C, E | 6 |
| H | D, F, G | 8 |
| I | C, E | 5 |
Пример 2. По данным таблицы 2 построить сетевой график.
Решение. Работы A, B и C не имеют предшествующих, поэтому реализация комплекса начинается с этих работ, и изображаются они дугами, выходящими из одного кружка - нулевого события (рис. 2). Масштаб при этом не соблюдается, и дуги А, В, С располагаются достаточно произвольно. Работе D предшествует работа А, поэтому дуга D на сети изображена вслед за дугой А. Далее надо изобразить работы E и F, выполняющиеся после работ А и В. Во избежание путаницы на сетях не рекомендуется изображать параллельными дугами одновременно выполняемые работы. В таких случаях условились вводить дополнительные события и фиктивные работы (нулевой продолжительности), которые изображаются штриховыми линиями. Их назначение – показать, что одна работа не может быть выполнена ранее какого-либо события или другой работы. Учитывая сказанное, введём фиктивную работу Аф, соединив конечное событие 1 работы А с конечным событием 2 работы В, и после этого изобразим работы Е и F дугами, выходящими из события 2. Дуги С и Е пришлось свести в одно событие 3, поскольку работы G и I могут начаться лишь после завершения работ С и Е.
А налогичным образом поступим и с дугами D, F и G, направив их в общее событие 4, имея в виду, что работа Н может начаться только после выполнения этих работ. И, наконец, дуги H и I моделируют заключительные работы комплекса (т.к. они не являются предшествующими ни для каких работ), а поэтому сведём их в одно завершающее событие 5. В конце следует проверить правильность нумерации событий (правило 8).
налогичным образом поступим и с дугами D, F и G, направив их в общее событие 4, имея в виду, что работа Н может начаться только после выполнения этих работ. И, наконец, дуги H и I моделируют заключительные работы комплекса (т.к. они не являются предшествующими ни для каких работ), а поэтому сведём их в одно завершающее событие 5. В конце следует проверить правильность нумерации событий (правило 8).
Расчёт параметров сетевой модели
′
 Существуют различные способы расчёта временных параметров сети. При небольших комплексах расчёты производятся вручную, при значительных – на компьютере. Рассмотрим способ расчёта параметров непосредственно на сети. При этом каждое событие изображается кружком, разделённым на четыре сектора (рис. 3), в которых по мере вычисления записываются следующие параметры:
Существуют различные способы расчёта временных параметров сети. При небольших комплексах расчёты производятся вручную, при значительных – на компьютере. Рассмотрим способ расчёта параметров непосредственно на сети. При этом каждое событие изображается кружком, разделённым на четыре сектора (рис. 3), в которых по мере вычисления записываются следующие параметры:
 - номер события;
- номер события;
 - ранний срок свершения события
- ранний срок свершения события  ;
;
 - поздний срок свершения события
- поздний срок свершения события  ;
;
 - резерв времени события
- резерв времени события  .
.
Определение. Любой путь, начало которого совпадает с исходным событием сети, а конец – с завершающим, представляет собой полный путь.
Определение. Полный путь максимальной продолжительности называется критическим. Он определяет время выполнения всего комплекса работ, которое называется критическим сроком и обозначается  . Работы и события, лежащие на критическом пути, называются критическими, остальные – некритическими.
. Работы и события, лежащие на критическом пути, называются критическими, остальные – некритическими.
Если выполнение какой-либо критической работы будет задержано, это вызовет задержку выполнения всего комплекса на тот же срок. Чтобы ускорить выполнение комплекса, необходимо сократить сроки выполнения критических работ. Некритические работы допускают некоторое запаздывание их выполнения без нарушения критического срока. Чтобы определить время, на которое можно задержать выполнение некритических работ, вводят понятия резервов времени событий и работ, которые, в свою очередь, выражаются через ранние и поздние сроки свершения событий.
Ранним сроком  свершения события
свершения события  называется самый ранний момент времени, к которому завершаются все работы, предшествующие этому событию.
называется самый ранний момент времени, к которому завершаются все работы, предшествующие этому событию.
Для исходного события 
 . Для всех других событий
. Для всех других событий  рассчитывается по формуле:
рассчитывается по формуле:  , (1.1)
, (1.1)
где  - ранний срок свершения начального события работы
- ранний срок свершения начального события работы  ;
;
 - продолжительность работы
- продолжительность работы  .
.
Итак, если событием  заканчивается одна работа, то
заканчивается одна работа, то  равен сумме
равен сумме  - раннего срока свершения её начального события – и
- раннего срока свершения её начального события – и  - продолжительности этой работы; если же событием
- продолжительности этой работы; если же событием  заканчивается несколько работ, то по каждой работе находится свой ранний срок, а искомым
заканчивается несколько работ, то по каждой работе находится свой ранний срок, а искомым  будет максимальный из них.
будет максимальный из них.
Поздним сроком  свершения события
свершения события  называется самый поздний момент времени, после которого остаётся ровно столько времени, сколько необходимо для завершения всех работ, следующих за этим событием.
называется самый поздний момент времени, после которого остаётся ровно столько времени, сколько необходимо для завершения всех работ, следующих за этим событием.
Для завершающего события 
 . Для всех других событий
. Для всех других событий  рассчитывается по формуле:
рассчитывается по формуле:  , (1.2)
, (1.2)
где  - поздний срок свершения конечного события работы
- поздний срок свершения конечного события работы  ;
;
 - продолжительность работы
- продолжительность работы  .
.
Итак, если событием  начинается одна работа, то
начинается одна работа, то  равен разности
равен разности  - позднего срока свершения её конечного события – и
- позднего срока свершения её конечного события – и  - продолжительности этой работы; если же событием
- продолжительности этой работы; если же событием  начинается несколько работ, то по каждой работе находится свой поздний срок, а искомым
начинается несколько работ, то по каждой работе находится свой поздний срок, а искомым  будет минимальный из них.
будет минимальный из них.
Разность между поздним и ранним сроками свершения события  составляет резерв
составляет резерв  времени этого события:
времени этого события:  .
.
Резерв  показывает, на какой предельно допустимый срок может задержаться свершение события
показывает, на какой предельно допустимый срок может задержаться свершение события  без изменения срока наступления завершающего события. Понятно, что у критических событий ранние и поздние сроки свершения совпадают, так что резерв времени у них равен нулю.
без изменения срока наступления завершающего события. Понятно, что у критических событий ранние и поздние сроки свершения совпадают, так что резерв времени у них равен нулю.
Определение критического пути
Работа  принадлежит критическому пути, если она находится между критическими событиями, т.е.
принадлежит критическому пути, если она находится между критическими событиями, т.е.  ,
,  и
и 
 .
.
 Зная сроки свершения событий, для работы
Зная сроки свершения событий, для работы  можно найти
можно найти
- ранний срок начала работы 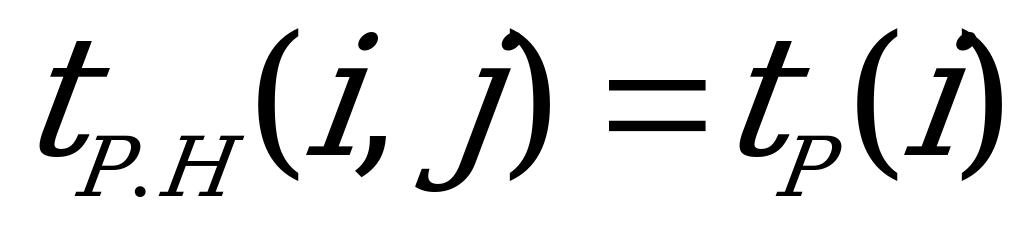 ,
,
- ранний срок окончания работы
ранний срок окончания работы  ,
,
- поздний срок окончания работы  ,
,
- поздний срок начала работы  ,
,
- полный резерв времени работы  .
.
 - это наибольший период времени, на который может быть задержано начало выполнения работы или увеличена её продолжительность без нарушения срока наступления завершающего события (без нарушения критического срока).
- это наибольший период времени, на который может быть задержано начало выполнения работы или увеличена её продолжительность без нарушения срока наступления завершающего события (без нарушения критического срока).

Пример 3. Для комплекса работ, представленного сетевым графиком (рис. 2), найти критический срок, критические работы и резервы времени некритических работ.
Решение. Расчёты проводятся в несколько этапов.
I этап. При вычислении  перемещаются по сети от события 0 к событию 5 в порядке возрастания номеров. Поскольку
перемещаются по сети от события 0 к событию 5 в порядке возрастания номеров. Поскольку  , в левый сектор кружка 0 записываем 0. Затем рассматривается событие 1, в которое входит работа (0,1). В соответствие с формулой (1.1)
, в левый сектор кружка 0 записываем 0. Затем рассматривается событие 1, в которое входит работа (0,1). В соответствие с формулой (1.1)  ;
;
это число и записываем в левый сектор кружка 1. При вычислении  учитываем, что в событие 2 входят две работы: (0,2) и (1,2). (Особо подчеркнём, что во всех расчётах фиктивные работы учитываются наряду с реальными!). Из формулы (1.1) получаем:
учитываем, что в событие 2 входят две работы: (0,2) и (1,2). (Особо подчеркнём, что во всех расчётах фиктивные работы учитываются наряду с реальными!). Из формулы (1.1) получаем:
 ,
,
что и записываем в левый сектор кружка 2. Аналогично вычисляем ранние сроки и остальных событий, в том числе  , т.е. критический срок. Итак,
, т.е. критический срок. Итак,  .
.
II этап. При вычислении поздних сроков свершения событий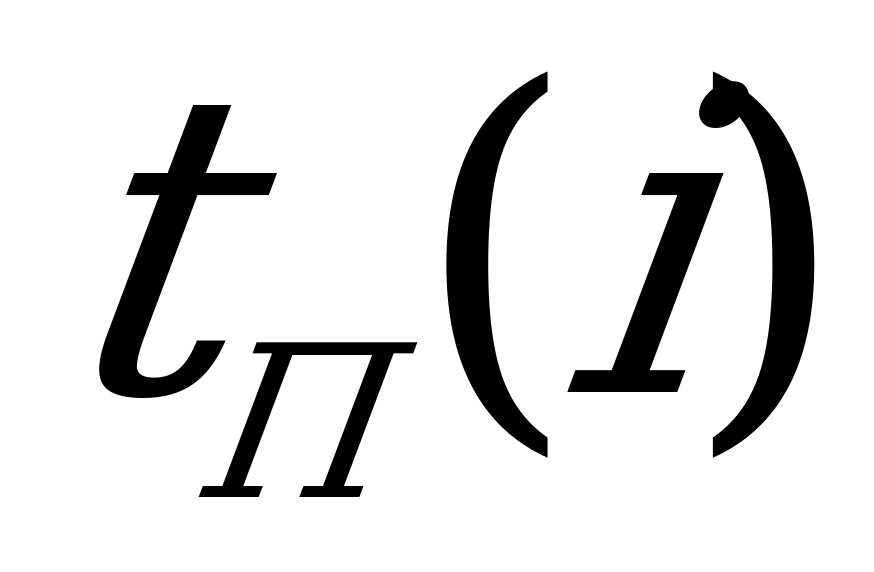 перемещаются по сети от события 5 к событию 0 в порядке убывания номеров. Поскольку
перемещаются по сети от события 5 к событию 0 в порядке убывания номеров. Поскольку  , в правый сектор кружка 5 записываем число
, в правый сектор кружка 5 записываем число  . Теперь рассматриваем событие 4, из которого выходит только одна работа (4,5). Следовательно, по формуле (1.2):
. Теперь рассматриваем событие 4, из которого выходит только одна работа (4,5). Следовательно, по формуле (1.2):  .
.
Этот результат и записываем в правый сектор кружка 4. Из события 3 выходят две работы (3,4) и (3,5), поэтому  ,
,
что и записываем в правый сектор кружка 3. Аналогично определяются поздние сроки свершения всех остальных событий сети. Заметим, что результатом расчётов должно быть равенство  .
.
III этап. Для определения резервов времени событий  достаточно из чисел, записанных в правых секторах кружков, вычесть числа, записанные в левых секторах, и заполнить нижние секторы.
достаточно из чисел, записанных в правых секторах кружков, вычесть числа, записанные в левых секторах, и заполнить нижние секторы.
IV этап. У критических событий резерв времени равен нулю. В нашем примере критическими являются события 0, 2, 4 и 5, они и определяют критические работы и критический путь 0─2─4─5. В данном примере критический путь на сети оказался единственным. Их может быть несколько. Заметим ещё, что критический путь может включать и фиктивные работы.
V этап. Все остальные параметры (сроки начала и окончания работ, резервы времени работ) выражаются через  и
и  , а потому легко могут быть вычислены. Результаты расчётов приведены в таблице 3.
, а потому легко могут быть вычислены. Результаты расчётов приведены в таблице 3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Таблица 3 |
|
|
| Работа 
| Продолжи-тельность  | Раннее | Позднее | Полный резерв 
|
|
|
| начало | окончание | начало | окончание |
|
|
| 
| 
| 
| 
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
| | | | | | | | | по графику | (2) + (3) | (6) - (2) | по графику | (6) - (3) - (2) |
|
|
| A (0-1) | 3 |
| 0 |
|
| 3 |
|
| 3 |
|
| 6 |
|
| 3 |
|
|
|
| B (0-2) | 6 |
| 0 |
|
| 6 |
|
| 0 |
|
| 6 |
|
| 0 |
|
|
|
| C (0-3) | 4 |
| 0 |
|
| 4 |
|
| 5 |
|
| 9 |
|
| 5 |
|
|
|
| D (1-4) | 5 |
| 3 |
|
| 8 |
|
| 10 |
|
| 15 |
|
| 7 |
|
|
|
| E (2-3) | 1 |
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 2 |
|
|
|
| F (2-4) | 9 |
| 6 |
|
| 15 |
|
| 6 |
|
| 15 |
|
| 0 |
|
|
|
| G (3-4) | 6 |
| 7 |
|
| 13 |
|
| 9 |
|
| 15 |
|
| 2 |
|
|
|
| H (4-5) | 8 |
| 15 |
|
| 23 |
|
| 15 |
|
| 23 |
|
| 0 |
|
|
|
| I (3-5) | 5 |
| 7 |
|
| 12 |
|
| 18 |
|
| 23 |
|
| 11 |
|
|
Например,  ;
;
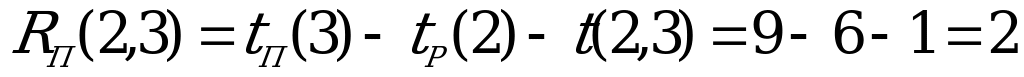 .
.
Построение календарного (линейного) графика
При анализе и оптимизации комплекса работ наряду с сетевым графиком применяется линейный график. Построить его можно по данному сетевому графику.
Каждая работа на линейном графике изображается в привязке к оси времени прямолинейным отрезком, длина которого в выбранном масштабе равна продолжительности  её выполнения.
её выполнения.
Прежде всего определяются календарные сроки выполнения критических работ.
Далее рассматриваются некритические работы.
Календарный график для таблицы 3
I
3
5






3
G
4






2
3
E






C
3




0


0
B
2
F
4
H
5







R


п










D
0
А








0
1
3
6
15
23
дни

9
1
1
4
П рактическая работа по теме:
рактическая работа по теме:
«Сетевое планирование и управление».
Задание. Составить сетевой график выполнения комплекса работ, рассчитать его параметры. Найти критический путь. Построить календарный (линейный) график.
Дано: перечень работ. Решение.
| Работа (обозначение) | Непосредственно предшествующие работы | Продолжительность работы |
| A | | 4 |
| B | A | 7 |
| C | A | 6 |
| D | B | 5 |
| E | B | 4 |
| F | C | 9 |
| G | D | 6 |
| H | E, F | 3 |
| I | C, G, H | 10 |
| K | D | 8 |
| L | K | 5 |
Сетевой график

Расчёт параметров

 - номер события
- номер события
 - ранний срок свершения события
- ранний срок свершения события 
 - поздний срок свершения события
- поздний срок свершения события 
 - резерв времени события
- резерв времени события 

Данный сетевой график содержит два критических пути: A─B─D─G─I, A─C─F─H─I.
Время, необходимое для выполнения всего комплекса работ, 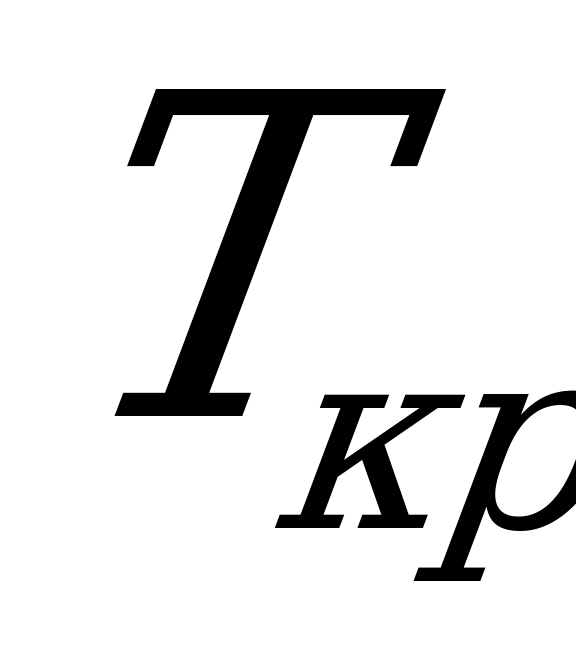 составляет 32 дня.
составляет 32 дня.
Календарный график
































L
5




0
3


















7
K
0
дни






2



1
5
6
8
8
7
A
B
D
G
I
1
4
6
C
F
H
3
4
E
4
10
19
22
32
16
27
У некритических работ E, K и L имеются резервы времени 4, 3 и 3 дня соответственно.







 Под событием понимают результат завершения одной или нескольких работ. При этом предполагается, что событие не имеет продолжительности, оно констатирует факт выполнения одной или нескольких работ (рис. 1).
Под событием понимают результат завершения одной или нескольких работ. При этом предполагается, что событие не имеет продолжительности, оно констатирует факт выполнения одной или нескольких работ (рис. 1).
 . Если работы А, В и С выполняются последовательно, то они изображаются следующим образом.
. Если работы А, В и С выполняются последовательно, то они изображаются следующим образом.
 . Если для выполнения работы С необходимы результаты работ А и В, то это изображается следующим образом.
. Если для выполнения работы С необходимы результаты работ А и В, то это изображается следующим образом. . В сети не должно быть ни одного события, из которого не выходит ни одной работы, кроме завершающего.
. В сети не должно быть ни одного события, из которого не выходит ни одной работы, кроме завершающего.  налогичным образом поступим и с дугами D, F и G, направив их в общее событие 4, имея в виду, что работа Н может начаться только после выполнения этих работ. И, наконец, дуги H и I моделируют заключительные работы комплекса (т.к. они не являются предшествующими ни для каких работ), а поэтому сведём их в одно завершающее событие 5. В конце следует проверить правильность нумерации событий (правило 8).
налогичным образом поступим и с дугами D, F и G, направив их в общее событие 4, имея в виду, что работа Н может начаться только после выполнения этих работ. И, наконец, дуги H и I моделируют заключительные работы комплекса (т.к. они не являются предшествующими ни для каких работ), а поэтому сведём их в одно завершающее событие 5. В конце следует проверить правильность нумерации событий (правило 8).  Существуют различные способы расчёта временных параметров сети. При небольших комплексах расчёты производятся вручную, при значительных – на компьютере. Рассмотрим способ расчёта параметров непосредственно на сети. При этом каждое событие изображается кружком, разделённым на четыре сектора (рис. 3), в которых по мере вычисления записываются следующие параметры:
Существуют различные способы расчёта временных параметров сети. При небольших комплексах расчёты производятся вручную, при значительных – на компьютере. Рассмотрим способ расчёта параметров непосредственно на сети. При этом каждое событие изображается кружком, разделённым на четыре сектора (рис. 3), в которых по мере вычисления записываются следующие параметры: Зная сроки свершения событий, для работы
Зная сроки свершения событий, для работы  ранний срок окончания работы
ранний срок окончания работы 



























 рактическая работа по теме:
рактическая работа по теме:





















































