Симметрия в кубе, параллелепипеде, призме и пирамиде

Презентация на тему: «Симметрия в кубе, параллелепипеде, призме и пирамиде».

Симметрия  – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).

Понятие симметрии включает в себя составные части – элементы симметрии. Сюда относятся  плоскость симметрии ,  ось симметрии ,  центр симметрии .

Симметрия в кубе

Оси симметрии в кубе:

  - прямые, проходящие через центры противоположных граней(таких 3) – прямые, проходящие через середины противоположных рёбер(таких 6).

Плоскости симметрии в кубе  - плоскости, проходящие через любые две оси симметрии.

  Плоскостей симметрии у куба   9. Проходят они либо через противоположные ребра (таковых плоскостей 6), либо через середины противоположных ребер (таких - 3).

Центр симметрии куба - точка пересечения его диагоналей.

Через центр симметрии проходят  9 осей симметрии.

Симметрия в параллелепипеде

У  прямоугольного параллелепипеда , как у всякого параллелепипеда,   центр симметрии  — точка пересечения его диагоналей, плоскости симметрии ( таких 3), проходящие через центр симметрии параллельно граням. На рисунке показана одна из таких плоскостей. Она проходит через середины четырех параллельных ребер параллелепипеда. Концы ребер являются симметричными точкам.

Симметрия в призме

1.  Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы

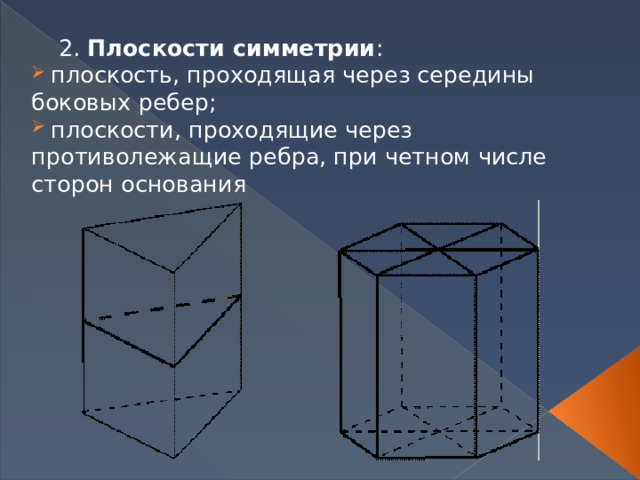
2. Плоскости симметрии :

• плоскость, проходящая через середины боковых ребер;
• плоскости, проходящие через противолежащие ребра, при четном числе сторон основания

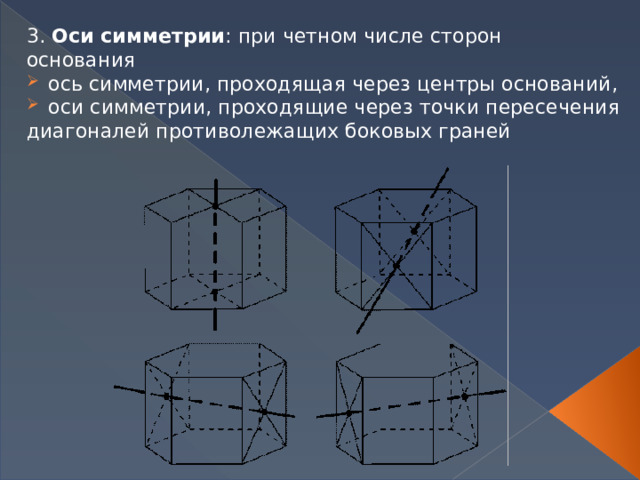
3.  Оси симметрии : при четном числе сторон основания 

• ось симметрии, проходящая через центры оснований,
• оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней

Симметрия в пирамиде

Симметрия правильной пирамиды

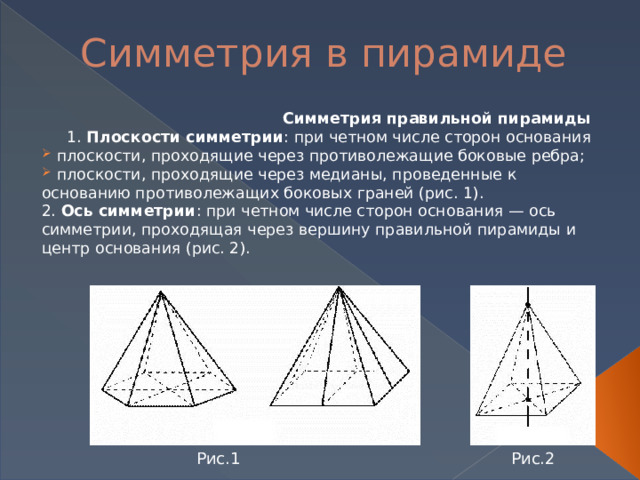
1. Плоскости симметрии : при четном числе сторон основания

• плоскости, проходящие через противолежащие боковые ребра;
• плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней (рис. 1).

2. Ось симметрии : при четном числе сторон основания — ось симметрии, проходящая через вершину правильной пирамиды и центр основания (рис. 2).

Рис.2

Рис.1