Симметрия в пространстве. Правильные многогранники

Дата: 31.03.2020

Тема: СИММЕТРИЯ В ПРОСТРАНСТВЕ. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.

Цели: ознакомить учащихся с симметрией в пространстве; ввести понятие «правильного многогранника».

Ход урока.

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Понятие «симметрия» для нас не новое, мы уже изучали симметрию на плоскости. Давайте повторим. Ответьте устно.

1. Какие виды симметрии на плоскости мы изучили?

2. Что такое центральная симметрия? Какой алгоритм построения симметричной фигуры относительно центра симметрии?

3. Что такое осевая симметрия? Какой алгоритм построения симметричной фигуры относительно оси симметрии?

4. Что такое поворот фигуры? Какой алгоритм построения симметричной фигуры с помощью поворота?

5. Что такое параллельный перенос фигуры? Какой алгоритм построения симметричной фигуры с помощью параллельного переноса?

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Сейчас мы рассмотрим преобразование симметрии в пространстве. Как вы думаете, относительно какой фигуры, кроме точки и прямой, в пространстве можно рассмотреть преобразование симметрии? (Относительно плоскости).

 Откройте свои тетради, запишите число и тему урока. И выполните конспект. 

Определение. Точки А и A₁ называются симметричными относительно точки О (центр симметрии), если О - середина отрезка АА₁. Точка О считается симметричной самой себе.

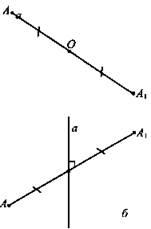
Определение. Точки А и А₁ называются симметричными относительно прямой а (ось симметрии), если прямая а проходит через середину отрезка АА₁ и перпендикулярна к этому отрезку. Каждая точка прямой а считается симметричной самой себе.

Определение. Точки А и А₁ называются симметричными относительно плоскости α (плоскость симметрии), если плоскость α проходит через середину отрезка АА₁ и перпендикулярна к этому отрезку. Каждая точка плоскости α считается симметричной самой себе.

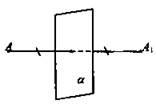
Обобщение. Итак, точка называется центром симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр симметрии, то говорят, что она обладает центральной симметрией.

 Прямая называется осью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет ось симметрии, то говорят, что она обладает осевой симметрией.     

Плоскость называется плоскостью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет плоскость симметрии, то говорят, что она обладает зеркальной симметрией.

Определение. Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно неё некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Определение. Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Откройте учебники на странице 77 и рассмотрите некоторые примеры правильных многогранников рис. 88-92.

Для более успешного закрепления материала посмотрите видеоурок, который находится по ссылке https://www.youtube.com/watch?v=d7u7D3N6HpI

Элементы симметрии куба.

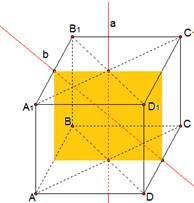
-куб со­став­лен из шести квад­ра­тов; квад­рат – это пра­виль­ный мно­го­уголь­ник;

-каж­дая вер­ши­на – это вер­ши­на трех квад­ра­тов, на­при­мер вер­ши­на А – общая для гра­ней-квад­ра­тов ABCD,  ;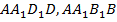

-сум­ма всех плос­ких углов при каж­дой вер­шине со­став­ля­ет 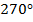 , т. к. со­сто­ит из трех пря­мых углов. Это мень­ше  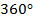, что удо­вле­тво­ря­ет по­ня­тию пра­виль­но­го мно­го­гран­ни­ка;

-куб имеет центр сим­мет­рии – точка пе­ре­се­че­ния диа­го­на­лей;

-куб имеет оси сим­мет­рии, на­при­мер пря­мые а и b, где пря­мая а про­хо­дит через се­ре­ди­ны про­ти­во­по­лож­ных гра­ней, а b – через се­ре­ди­ны про­ти­во­по­лож­ных ребер;

-куб имеет плос­ко­сти сим­мет­рии, на­при­мер плос­кость, ко­то­рая про­хо­дит через пря­мые а и b.

3. ПРАКТИЧЕСКАЯ ЧАСТЬ

Выполним все вместе № 279. Прочтите условие задачи. Выполним рисунок.

№ 279

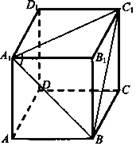
Дано: ABCDA₁B₁C₁D₁ – куб, А₁В и A₁C₁ - диагонали граней куба, имеющие общий конец.

Найти: ∠ВА₁С₁.

Решение:

1) Введем обозначения. Пусть а - длина ребра куба. Так как все грани куба - равные квадраты, то диагонали граней равны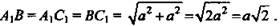 

2) Рассмотрим ΔA₁BС₁ - равносторонний, значит, ∠BA₁C₁ = 60°.

Ответ: 60°.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Какие существуют виды симметрии в пространстве? Какой многогранник называется правильным? Какие правильные многогранники вы знаете?

Домашнее задание: стр. 75-79 читать, №276+ТВОРЧЕСКОЕ ЗАДАНИЕ.

Согласно нумерации ваших фамилий в списке классного журнала выполняем:

№ по списку 1, 5, 8, 9, 13, 17, 21 - №272,

№ по списку 2, 4, 6, 10, 14, 16, 18 – №273,

№ по списку 3, 7, 11, 12, 15, 19, 20 - №274.