Система счисления и их применение

Муниципальное бюджетное общеобразовательное учреждение средняя образовательная школа № 4  

с. Верхнеяркеево

Системы счисления и их применение

Аглямова Алия Рамилевна

Цель

Изучить роль двоичной системы счисления и познакомиться с иными системами счисления.

Задачи

• изучить литературу о различных системах счисления,
• провести анкетирование учащихся
• подробнее рассмотреть двоичную

систему счисления,

• узнать чем удобна двоичная система

счисления и где она используется.

Арифметика каменного века

Бирки – долговые расписки у многих народов

Кипу - узелки для запоминания численной информации у инков

Шумерская система счисления

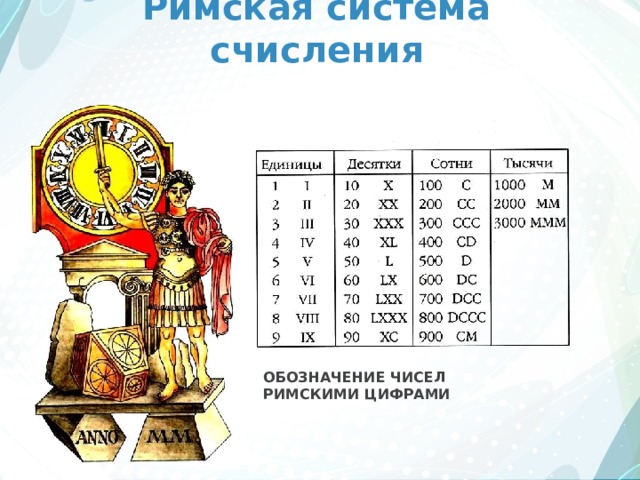
Римская система счисления

ОБОЗНАЧЕНИЕ ЧИСЕЛ РИМСКИМИ ЦИФРАМИ

Система счисления Древней Руси

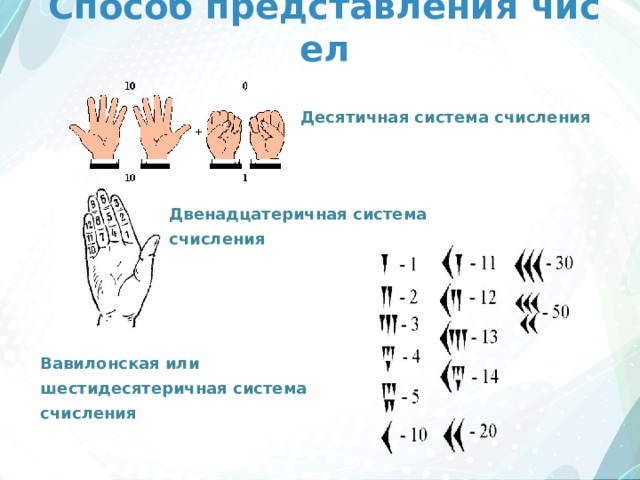
Способ представления чисел

Десятичная система счисления

Двенадцатеричная система счисления

Вавилонская или шестидесятеричная система счисления

• десятеричная, пятеричная, двенадцатеричная, двадцатеричная.
• десятеричная, пятеричная, двенадцатеричная, двадцатеричная.

• древнеармянская, древнегрузинская, древнегреческая, ионическая, славянская.
• древнеармянская, древнегрузинская, древнегреческая, ионическая, славянская.

• двоичная, восьмеричная, шестнадцатеричная.
• двоичная, восьмеричная, шестнадцатеричная.

• Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.
• Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.

Системы счисления различают:

Анатомического происхождения

Алфавитные

Машинные

Прочие

Позиционные системы счисления

• В позиционных системах счисления величина, обозначается цифрой, зависит от места цифры в числе. Так в числе 222 цифра 2 встречается трижды. Но самая правая означает две единицы, вторая справа – два десятка и, наконец, третья – две сотни.
• В позиционных системах счисления величина, обозначается цифрой, зависит от места цифры в числе. Так в числе 222 цифра 2 встречается трижды. Но самая правая означает две единицы, вторая справа – два десятка и, наконец, третья – две сотни.

Непозиционные системы счисления

• В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели. Примером непозиционный системы счисления является римская система счисления.
• В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели. Примером непозиционный системы счисления является римская система счисления.

Сравнение систем счисления

Результаты анкетирования

Лейбниц Готфрид Вильгельм

21 июня (1 июля) 1646 г. — 14 ноября 1716 г.

Саксонский философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед.

Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук.

Спасибо за внимание!