РАЗДЕЛ: «ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЁННОСТИ»
Ранее рассматривались задачи, в которых лицо, принимающее решение, обладает всей необходимой информацией. Такие задачи называются детерминированными (или задачами принятия решений в условиях определённости).
Ограниченность или неточность информации приводит к появлению в задаче случайных величин. Они называются задачами принятия решений в условиях неопределённости, для которых возможна одна из двух ситуаций: 1) законы распределения соответствующих случайных величин либо известны, либо могут быть определены (такие задачи называются стохастическими или задачами принятия решений в условиях риска); 2) информация о законах распределения случайных величин неизвестна.
Таким образом, по отношению к исходной информации определённость и полная неопределённость представляют собой два крайних случая, а риск определяет промежуточную ситуацию.
Одним из примеров задач стохастического программирования являются задачи теории массового обслуживания, предметом которой является изучение работы своеобразных систем, называемых системами массового обслуживания (СМО).
Вторым случаем неопределённости, когда некоторые параметры, от которых зависит выбор решения, неизвестны, и нет никаких данных о том, какие их значения более, а какие – менее вероятны, занимаются специальные разделы математики: «Теория игр» и «Теория статистических решений».
СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ
Основные понятия. Классификация систем массового обслуживания
Своеобразный класс стохастических (вероятностных) моделей образуют модели массового обслуживания, отражающие особенности поведения систем, подвергающихся воздействию потока тех или иных событий. Сама такая система называется обслуживающей, или системой массового обслуживания (СМО).
СМО встречаются практически везде, где есть или может возникнуть очередь. На Западе методы массового обслуживания даже получили название «теория очередей».
Впервые такую задачу поставил датский математик Эрланг в начале ХХ века для анализа работы телефонной станции. Примерами СМО являются также магазины, ремонтные мастерские, билетные кассы, парикмахерские, вычислительные комплексы и т.п.
Каждая СМО состоит из какого-то числа обслуживающих единиц, которые называются каналами (или приборами) обслуживания. Каналами могут быть линии связи, рабочие точки, продавцы, кассиры, лифты, вычислительные машины и др.
Заявки поступают в СМО в какие-то случайные моменты времени, образуя так называемый случайный поток заявок (требований). Обслуживание заявки продолжается, вообще говоря, также какое-то случайное время, после чего канал освобождается и готов к приёму следующей заявки. Случайный характер потока заявок и времени обслуживания каждой заявки приводит к тому, что в какие-то периоды времени на входе СМО скапливается большое число заявок (они либо становятся в очередь, либо покидают СМО необслуженными), в другие же периоды СМО работает с недогрузкой или вообще простаивает.
Предметом теории массового обслуживания является построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, характер потока заявок и т.п.) с показателями эффективности СМО, описывающими её способность справляться с потоком заявок.
В качестве показателей эффективности СМО используются:
- среднее число заявок, обслуживаемых в единицу времени;
- среднее число заявок в очереди;
- среднее время ожидания заявки в очереди;
- вероятность отказа в обслуживании;
- вероятность того, что число заявок в очереди превысит определённое значение и т.п.
Блок обслуживания
Выходной поток
(обслуженные
заявки)
С

Входной поток
заявок
Очередь
* * * * *
ПО 1
труктура СМО показана на рисунке.







ПО 2

……..

Необслуженные
заявки
ПО n
 ,
, 
 - интенсивность (плотность) потока,
- интенсивность (плотность) потока,
 =
= +
+ ;
;
 - число мест в очереди;
- число мест в очереди;
 - количество приборов (каналов) обслуживания;
- количество приборов (каналов) обслуживания;
 - среднее время обслуживания одной заявки.
- среднее время обслуживания одной заявки.
Системы массового обслуживания делятся на типы (или классы) по ряду признаков.
В зависимости от числа мест в очереди  СМО разделяются на:
СМО разделяются на:
системы без очереди (без ожидания) ( =0) – в таких СМО всякая вновь поступившая заявка, застав все ПО занятыми, получает отказ и покидает систему необслуженной (примеры таких СМО встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы заняты, получает отказ);
=0) – в таких СМО всякая вновь поступившая заявка, застав все ПО занятыми, получает отказ и покидает систему необслуженной (примеры таких СМО встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы заняты, получает отказ);
системы с очередью (с ожиданием) ( ) - в таких СМО заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.
) - в таких СМО заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь на обслуживание.
СМО с очередью подразделяются на разные виды в зависимости от того, как организована очередь (ограничения могут касаться как длины очереди, так и времени ожидания заявки в очереди):
а) СМО с ограниченной очередью,
б) СМО с неограниченной очередью;
а) СМО с ограниченным временем ожидания,
б) СМО с неограниченным временем ожидания;
в зависимости от дисциплины обслуживания очереди, определяющей порядок выбора заявок из числа поступивших, системы подразделяются на:
а) СМО с обслуживанием в порядке поступления («первой пришла – первой обслуживаешься»),
б) СМО с обслуживанием в обратном порядке («последней пришла – обслуживаешься первой») – например, стек в программировании;
в) СМО со случайным порядком обслуживания, т.е. заявка выбирается из общего списка ожидающих случайным образом.
Нередко встречается так называемое обслуживание с приоритетом (когда в первую очередь обслуживаются наиболее важные заявки); приоритет может быть как абсолютным, когда заявка с более высоким приоритетом «вытесняет» из-под обслуживания обычную заявку (например, в случае аварийной ситуации плановые работы ремонтной бригады прерываются до ликвидации аварии), так и относительным, когда начатое обслуживание доводится до конца, а заявка с более высоким приоритетом получает лишь «лучшее» место в очереди.
В зависимости от числа каналов (приборов) обслуживания  СМО разделяются на:
СМО разделяются на:
одноканальные ( ) и многоканальные (
) и многоканальные ( ).
).
Под каналом (прибором) обслуживания имеется в виду устройство или человек, обслуживающий заявки. Например, билеты в кинотеатре могут продаваться в одной или нескольких кассах. В первом случае СМО называют одноканальной, во втором - многоканальной.
В зависимости от количества заявок, которое может обслуживать ПО одновременно, СМО разделяются на:
системы с обслуживанием в режиме разделения времени,
системы с пакетным обслуживанием.
Например, лифт высотного здания обслуживает сразу несколько человек, а кассир в магазине – только одного.
В зависимости от количества ПО, которыми должна быть обслужена заявка, СМО разделяются на:
однофазные и многофазные.
В первом случае заявка обслуживается только одним ПО, после чего покидает систему. Во втором случае заявка должна пройти некоторую последовательность приборов, т.е. обслуживание заявки состоит из нескольких последовательных этапов или «фаз» (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, затем получить на контроле).
В зависимости от источника потока требований СМО разделяются на:
открытые (разомкнутые) и замкнутые.
Разомкнутая система – эта система с неограниченным источником потока заявок (например, покупатели в магазинах, пассажиры в метро и т.д.).
Замкнутая система – эта система, в которой поток требований ограничен (например, система наладки станков в цехе; каждый станок в будущем становится потенциальным источником заявок на подналадку). В таких системах общее число циркулирующих заявок конечно и чаще всего постоянно.
Понятие марковского случайного процесса
Процесс работы СМО представляет собой случайный процесс. Говорят, что в системе  протекает случайный процесс, если система меняет своё состояние с течением времени (переходит из одного состояния в другое) заранее неизвестным, случайным образом. Под системой может пониматься техническое устройство, предприятие, отрасль промышленности, живой организм, популяция и т.д.
протекает случайный процесс, если система меняет своё состояние с течением времени (переходит из одного состояния в другое) заранее неизвестным, случайным образом. Под системой может пониматься техническое устройство, предприятие, отрасль промышленности, живой организм, популяция и т.д.
Большинству процессов, протекающих в реальных системах, свойственны в той или иной мере черты случайности, неопределённости. Строго говоря, все процессы в природе случайны, им присущи некоторые случайные возмущения. Но до тех пор, пока эти возмущения несущественны, мало влияют на интересующие нас параметры, мы можем ими пренебречь и рассматривать процесс как детерминированный, неслучайный. Необходимость учёта случайностей возникает тогда, когда они прямо касаются нашей заинтересованности. Например, составляя расписание самолётов, можно пренебречь случайными колебаниями самолёта около центра массы, а проектируя автопилот - безусловно, нет.
Процесс называется процессом с дискретными состояниями, если его возможные состояния 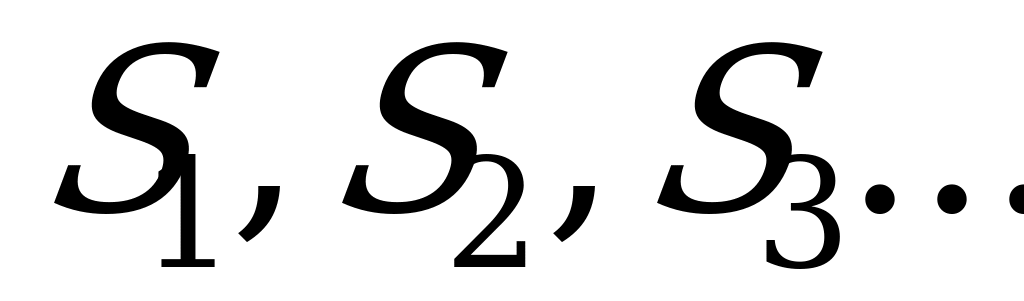 можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком).
можно заранее перечислить, а переход системы из состояния в состояние происходит мгновенно (скачком).
Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из состояния в состояние не фиксированы заранее, а случайны (т.е. переход может осуществиться, в принципе, в любой момент).
Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем; состояние СМО меняется скачком в моменты появления каких-то событий (прихода новой заявки, окончания обслуживания заявки, момента, когда заявка, которой надоело ждать, покидает очередь).
Математический анализ работы СМО существенно упрощается, если процесс этой работы – марковский.
Случайный процесс называется марковским (или случайным процессом без последействия), если для любого момента времени  вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент
вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент  и не зависят от того, когда и как система пришла в это состояние.
и не зависят от того, когда и как система пришла в это состояние.
Пример марковского процесса: система  - счётчик в такси. Состояние системы в момент
- счётчик в такси. Состояние системы в момент 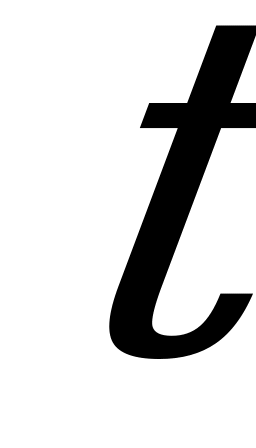 характеризуется числом километров, пройденных автомобилем до данного момента. Пусть в момент
характеризуется числом километров, пройденных автомобилем до данного момента. Пусть в момент  счётчик показывает
счётчик показывает  . Вероятность того, что в момент
. Вероятность того, что в момент  счётчик покажет то или иное число километров (точнее, соответствующее числу рублей), зависит от
счётчик покажет то или иное число километров (точнее, соответствующее числу рублей), зависит от  , но не зависит от того, в какие моменты времени изменялись показания счётчика до момента
, но не зависит от того, в какие моменты времени изменялись показания счётчика до момента  .
.
На практике марковские процессы в чистом виде обычно не встречаются, но нередко приходится иметь дело с процессами, для которых влиянием «предыстории» можно пренебречь.
В других случаях процесс можно рассматривать как марковский, если все параметры из «прошлого» включить в «настоящее». Например, пусть речь идёт о работе некоторого технического устройства; в какой-то момент  оно ещё исправно, и нас интересует вероятность того, что оно проработает ещё время
оно ещё исправно, и нас интересует вероятность того, что оно проработает ещё время  . Если за настоящее состояние системы считать просто «система исправна», то процесс безусловно не марковский, потому что вероятность того, что она не откажет за время
. Если за настоящее состояние системы считать просто «система исправна», то процесс безусловно не марковский, потому что вероятность того, что она не откажет за время  , зависит от того, сколько времени она уже проработала и когда был последний ремонт. Если оба эти параметра (общее время работы и время после последнего ремонта) включить в настоящее состояние системы, то процесс уже можно считать марковским.
, зависит от того, сколько времени она уже проработала и когда был последний ремонт. Если оба эти параметра (общее время работы и время после последнего ремонта) включить в настоящее состояние системы, то процесс уже можно считать марковским.
Граф состояний
При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – так называемым графом состояний. Состояния системы изображаются кружками (или прямоугольниками), а возможные переходы из состояния в состояние – ориентированными дугами, соединяющими состояния.
П ример. Построить граф состояний следующего случайного процесса. Техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное, случайное время.
ример. Построить граф состояний следующего случайного процесса. Техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное, случайное время.
Р е ш е н и е.
Возможные состояния системы:
 - оба узла исправны;
- оба узла исправны;
 - первый узел ремонтируется,
- первый узел ремонтируется,
второй исправен;
 - второй узел ремонтируется,
- второй узел ремонтируется,
первый исправен;
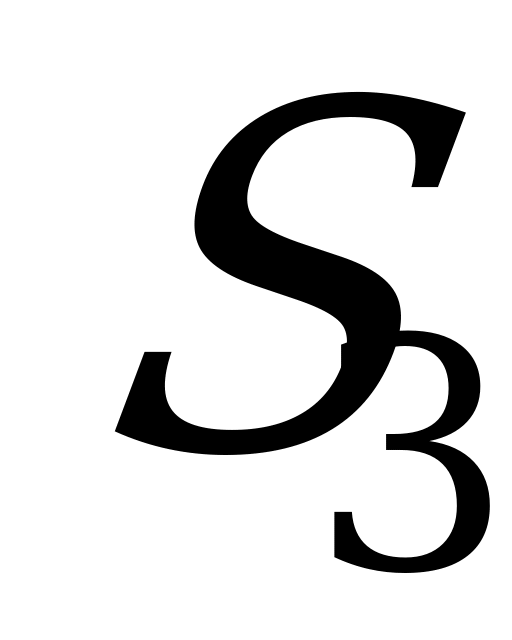 - оба узла ремонтируются.
- оба узла ремонтируются.
Дуга, направленная из  в
в  , означает переход системы в момент отказа первого узла; дуга, направленная обратно (из
, означает переход системы в момент отказа первого узла; дуга, направленная обратно (из  в
в  ) – переход системы в момент окончания ремонта этого узла. Остальные дуги объясняются аналогично.
) – переход системы в момент окончания ремонта этого узла. Остальные дуги объясняются аналогично.
На графе отсутствуют переходы из  в
в 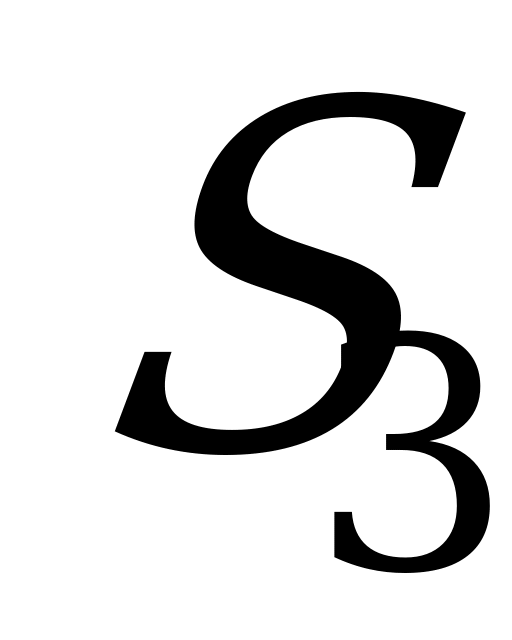 и из
и из  в
в  . Это объясняется тем, что выходы узлов из строя предполагаются независимыми друг от друга, и вероятностью одновременного выхода из строя двух узлов (переход из
. Это объясняется тем, что выходы узлов из строя предполагаются независимыми друг от друга, и вероятностью одновременного выхода из строя двух узлов (переход из  в
в 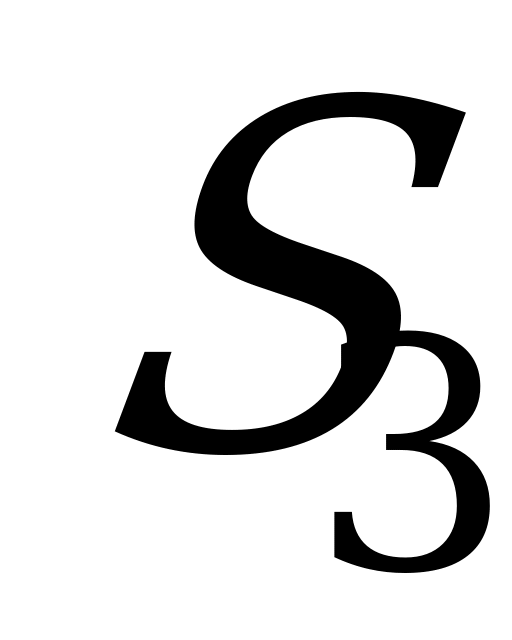 ) или одновременного окончания ремонтов двух узлов (переход из
) или одновременного окончания ремонтов двух узлов (переход из 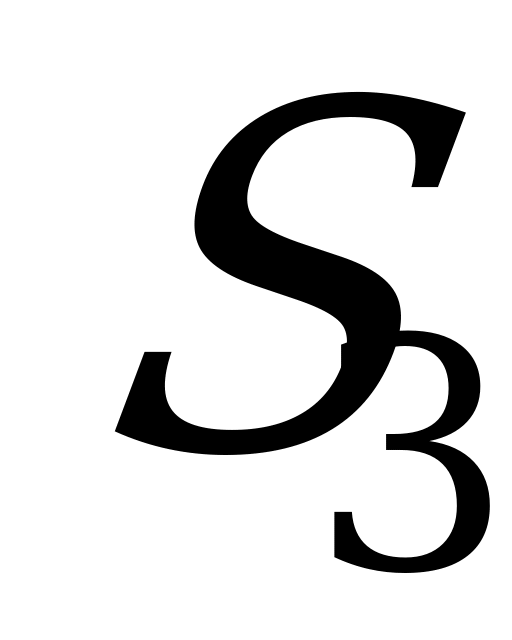 в
в  ) можно пренебречь.
) можно пренебречь.
На графе проставляются интенсивности 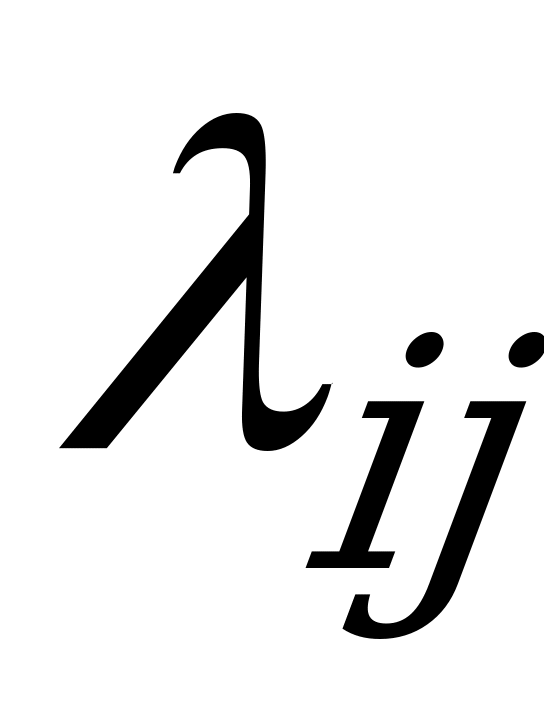 потоков событий, переводящих систему из состояния
потоков событий, переводящих систему из состояния  в состояние
в состояние  ; так, переход системы из
; так, переход системы из  в
в  происходит под воздействием потока отказов 1-го узла (интенсивностью
происходит под воздействием потока отказов 1-го узла (интенсивностью  ), а обратный переход (из
), а обратный переход (из  в
в  ) – под воздействием потока «окончаний ремонтов» 1-го узла (
) – под воздействием потока «окончаний ремонтов» 1-го узла ( ) и т.п.
) и т.п.
Потоки событий
Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Например, поток вызовов на телефонной станции; поток железнодорожных составов, поступающих на сортировочную станцию; поток частиц, падающих на счётчик Гейгера, и т.д.
Поток событий можно изобразить рядом точек на оси времени. Каждая точка 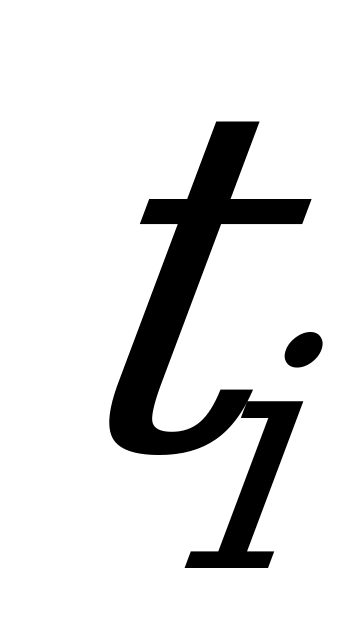 соответствует моменту появления
соответствует моменту появления 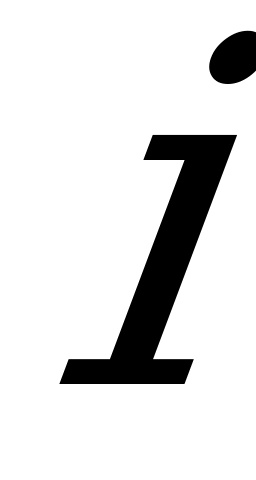 -го события.
-го события.



























0
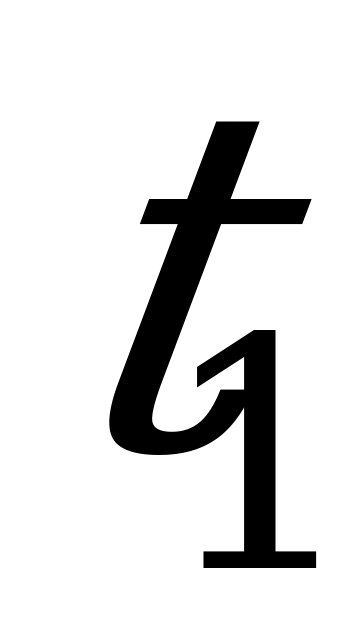 t1
t1
 t1
t1
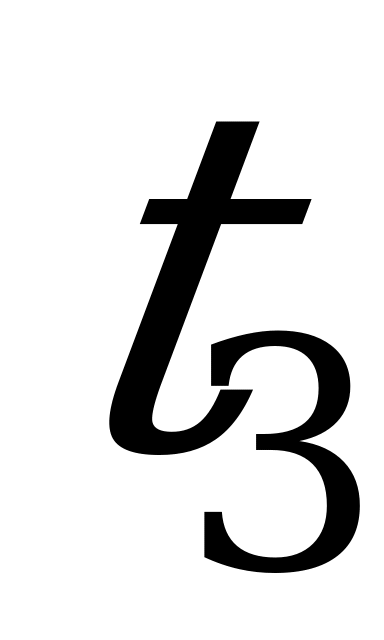 t1
t1
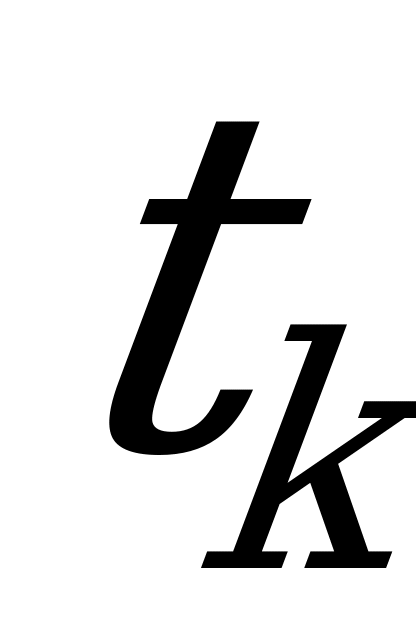 t1
t1
 t1
t1
Важной характеристикой потока событий является его интенсивность  - среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной (
- среднее число событий, приходящееся на единицу времени. Интенсивность потока может быть как постоянной ( ), так и переменной, зависящей от времени
), так и переменной, зависящей от времени 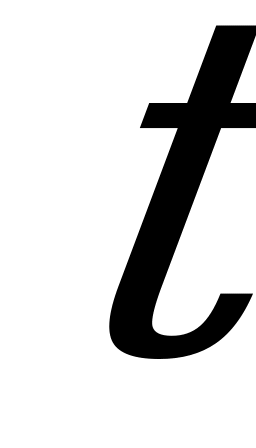 . Например, поток автомашин, движущихся по улице, днём интенсивнее, чем ночью, в часы пик - интенсивнее, чем в другие часы.
. Например, поток автомашин, движущихся по улице, днём интенсивнее, чем ночью, в часы пик - интенсивнее, чем в другие часы.
ℓ
ℓ
ℓ
ℓ
Поток событий называется
регулярным, если события следуют одно за другим через определённые,
равные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным.

0
 t1
t1
 t1
t1
 t1
t1
 t1
t1
 t1
t1























С первого взгляда может показаться, что регулярный поток представляет собой наиболее простой из всех возможных потоков событий. Однако это не так. Дело в том, что в регулярном потоке моменты появления последовательных событий связаны между собой жёсткой функциональной зависимостью. Это сильно затрудняет анализ явлений, в которых фигурирует одновременно большое число таких потоков.
Гораздо проще анализировать потоки событий, появляющихся в случайные моменты времени независимо друг от друга.
Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность  стационарного потока есть величина постоянная.
стационарного потока есть величина постоянная.
Это отнюдь не означает, что фактическое число событий, появляющееся в единицу времени, постоянно. Поток неизбежно (если только он не регулярный) имеет какие-то случайные сгущения и разрежения. На один участок длины 1 может попасть больше, а на другой – меньше событий, но среднее число событий, приходящееся на единицу времени, постоянно и от времени не зависит.
На практике часто встречаются потоки событий, которые (по крайней мере, на ограниченном участке времени) могут считаться стационарными. Например, поток вызовов, поступающих на АТС между 13 и 14 часами, практически стационарен; тот же поток в течение суток уже не стационарен.
Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени  и
и  число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, вызванные каждое своими собственными причинами. Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток поездов, подходящих к станции, уже имеет последействие, т.к. между ними всегда существует какой-то минимальный интервал
число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, вызванные каждое своими собственными причинами. Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток поездов, подходящих к станции, уже имеет последействие, т.к. между ними всегда существует какой-то минимальный интервал  , выбираемый из соображений безопасности. Впрочем, если минимальный интервал между событиями много меньше среднего интервала между ними
, выбираемый из соображений безопасности. Впрочем, если минимальный интервал между событиями много меньше среднего интервала между ними 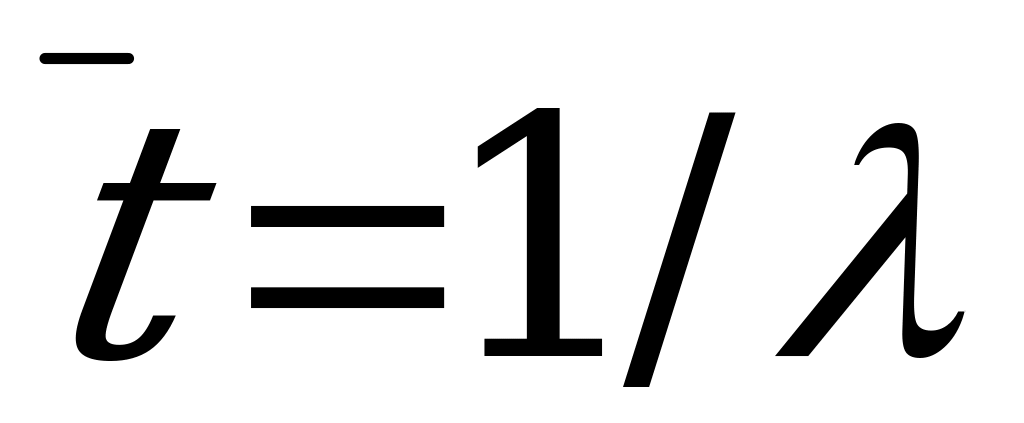 , иногда наличием последействия можно пренебречь.
, иногда наличием последействия можно пренебречь.
Поток событий называется ординарным, если события в нём появляются поодиночке, а не группами по нескольку сразу. Например, поток поездов, подходящих к станции, ординарен; а поток вагонов – неординарен. Если поток событий ординарен, то вероятностью попадания на малый участок времени 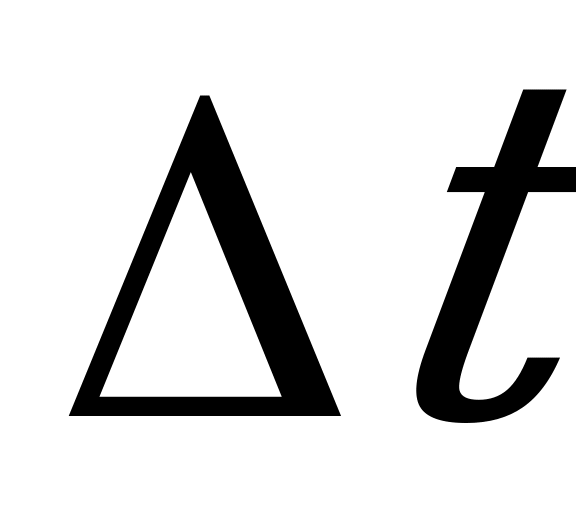 двух или более событий можно пренебречь.
двух или более событий можно пренебречь.
Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия.
Название «простейший» объясняется тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Простейший поток играет среди других потоков особую роль, в чём-то подобную роли нормального закона среди других законов распределения. А именно, при наложении достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему с интенсивностью  , равной сумме интенсивностей входящих потоков:
, равной сумме интенсивностей входящих потоков:
 .
.
Для простейшего потока с интенсивностью  число событий
число событий  , попадающих на произвольный участок времени
, попадающих на произвольный участок времени  , распределено по закону Пуассона
, распределено по закону Пуассона
 .
.
Очевидно, что для простейшего потока среднее число событий (математическое ожидание), приходящееся на участок  , пропорционально его длине
, пропорционально его длине  :
:
 ,
,
и не зависит от того, где именно на оси  выбран участок.
выбран участок.
Можно доказать, что для простейшего потока интервал  между соседними событиями имеет так называемое показательное распределение с плотностью
между соседними событиями имеет так называемое показательное распределение с плотностью
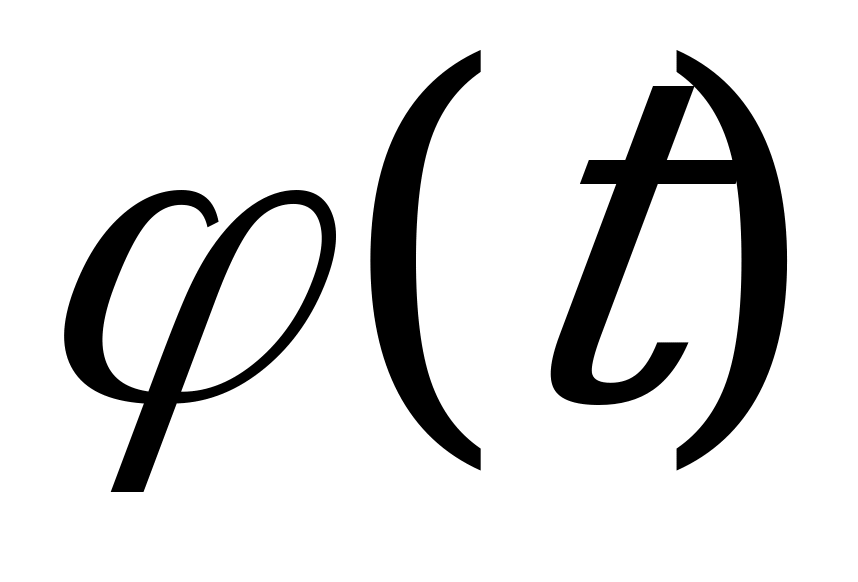

(

).
П

лотность распределения является функцией, интегрирование которой по интервалу даёт вероятность п




0



опадания случайной величины в этот интервал. Геометрически эта вероятность равняется площади соответствующей криволинейной трапеции.
Для случайной величины  , имеющей показательное распределение, математическое ожидание
, имеющей показательное распределение, математическое ожидание  равно среднему квадратическому отклонению
равно среднему квадратическому отклонению  и обратно по величине интенсивности потока
и обратно по величине интенсивности потока  :
:
 .
.
Для простейшего потока с интенсивностью  вероятность попадания на элементарный (малый) отрезок времени
вероятность попадания на элементарный (малый) отрезок времени 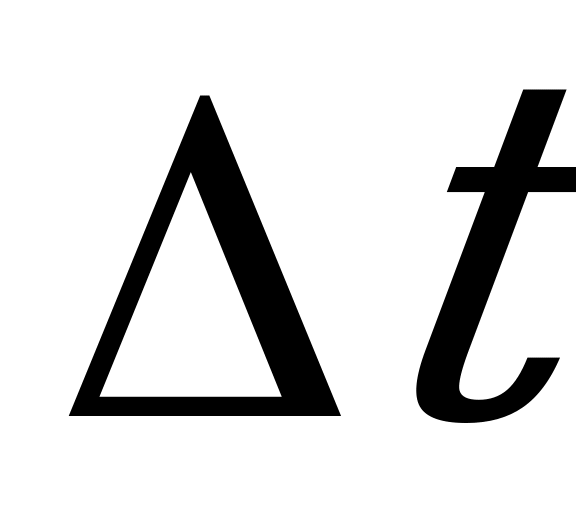 хотя бы одного события потока равна интенсивности потока, умноженной на длину элементарного участка:
хотя бы одного события потока равна интенсивности потока, умноженной на длину элементарного участка:
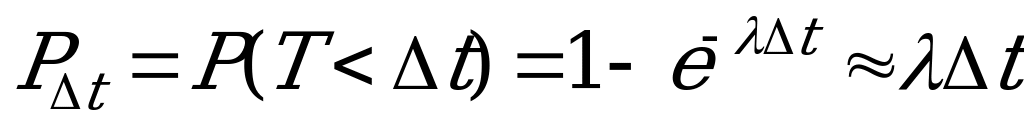 .
.
Эта приближённая формула, получаемая заменой функции 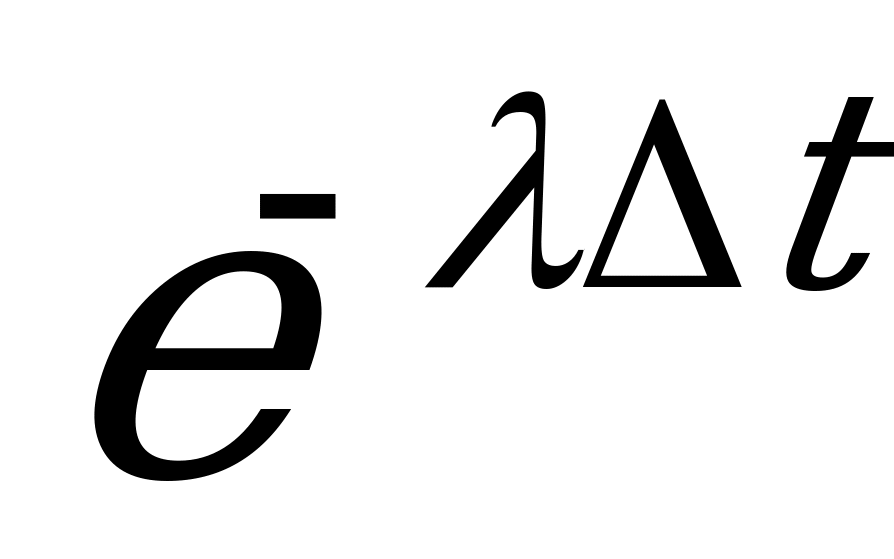 лишь двумя первыми членами её разложения в ряд по степеням
лишь двумя первыми членами её разложения в ряд по степеням 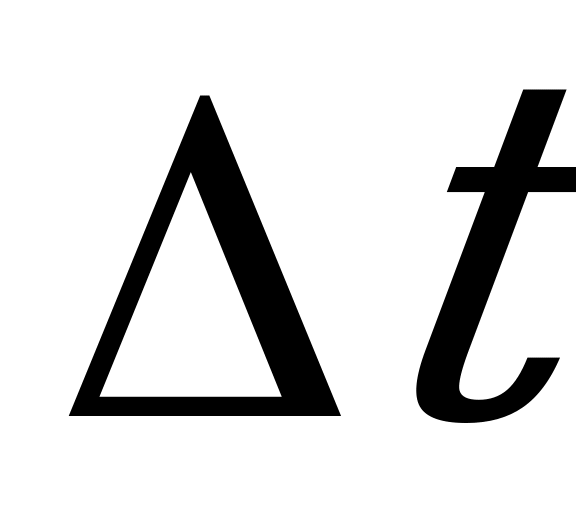 , тем точнее, чем меньше
, тем точнее, чем меньше 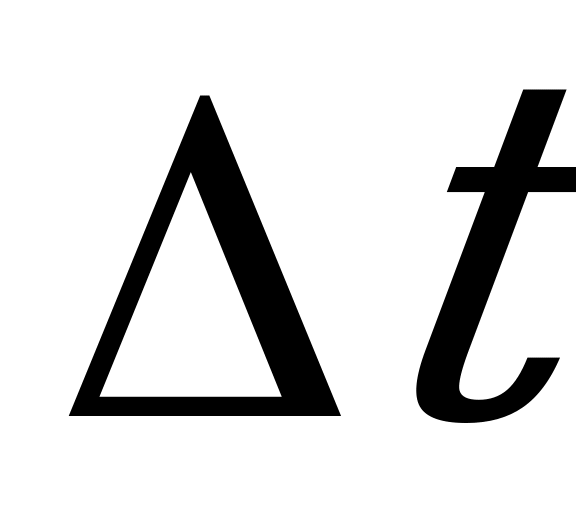 .
.
Уравнения Колмогорова для вероятностей состояний.
Финальные вероятности состояний
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно представлять, что все переходы системы  из состояния в состояние происходят под действием простейших потоков событий с интенсивностями
из состояния в состояние происходят под действием простейших потоков событий с интенсивностями 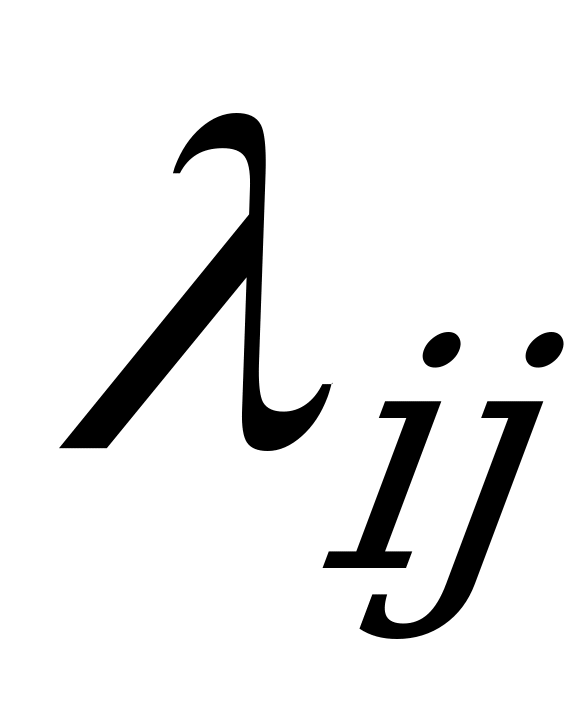 (поток вызовов, поток отказов, поток восстановлений и т.д.).
(поток вызовов, поток отказов, поток восстановлений и т.д.).
Вероятностью 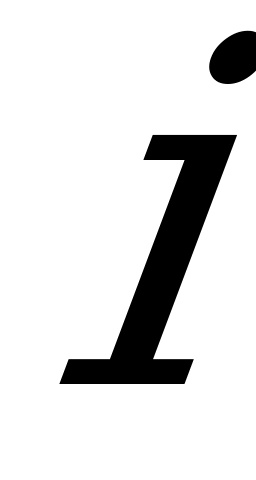 -го состояния называется вероятность
-го состояния называется вероятность  того, что в момент
того, что в момент 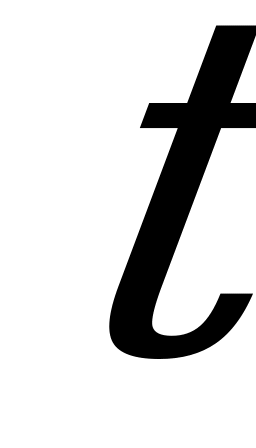 система будет находиться в состоянии
система будет находиться в состоянии  . Очевидно, что для любого момента
. Очевидно, что для любого момента 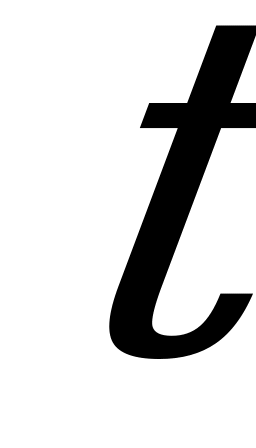 сумма вероятностей всех состояний равна единице:
сумма вероятностей всех состояний равна единице:
 .
.
Чтобы найти все вероятности состояний  , составляются и решаются так называемые уравнения Колмогорова. Это особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.
, составляются и решаются так называемые уравнения Колмогорова. Это особого вида дифференциальные уравнения, в которых неизвестными функциями являются вероятности состояний.
Правило составления уравнений Колмогорова: в левой части каждого из них стоит производная вероятности 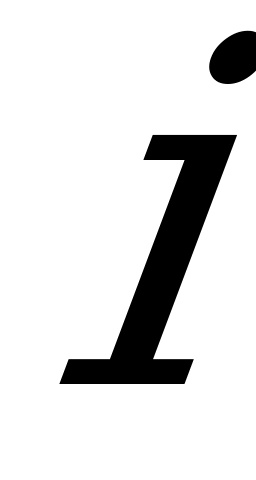 -го состояния; в правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (
-го состояния; в правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (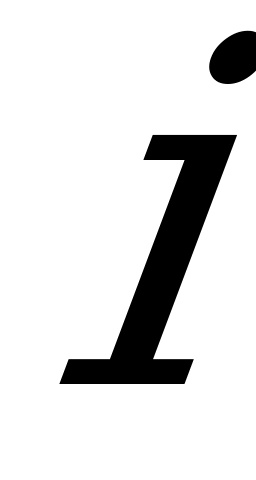 -го) состояния.
-го) состояния.
П
Система дифференциальных уравнений Колмогорова для вероятностей состояний:
ример.
Граф состояний













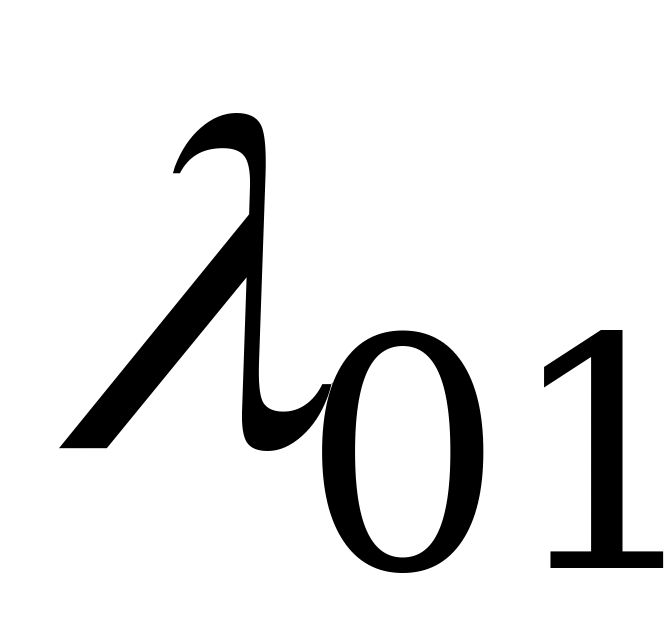
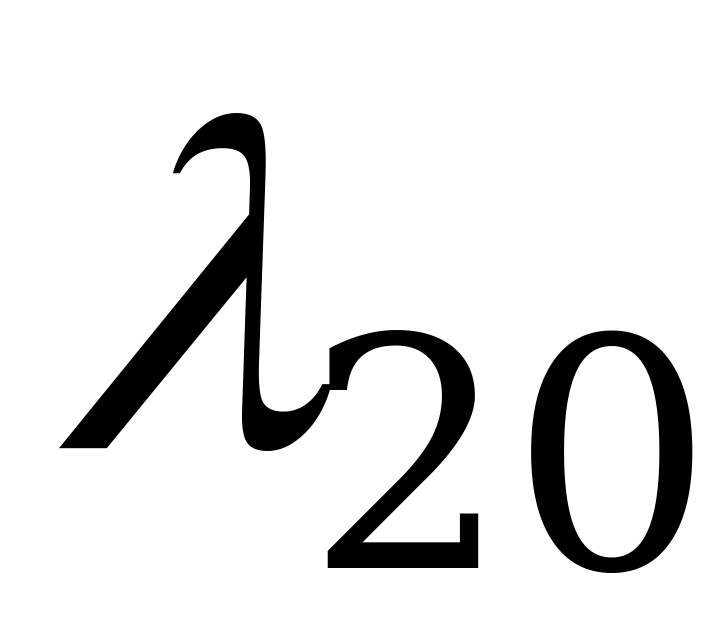




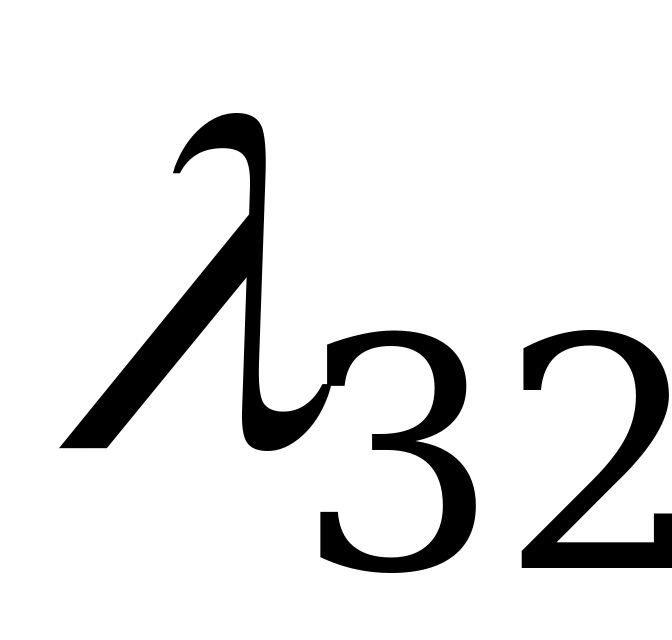






В полученной системе независимых уравнений на одно меньше общего числа уравнений. Поэтому для её решения одно из уравнений можно отбросить, пользуясь тем, что  (выразить любую из вероятностей
(выразить любую из вероятностей  через другие, это выражение подставить в систему уравнений, а соответствующее уравнение с производной
через другие, это выражение подставить в систему уравнений, а соответствующее уравнение с производной  отбросить).
отбросить).
Особенность решения дифференциальных уравнений состоит в том, что требуется задать так называемые начальные условия, т.е. вероятности состояний системы в начальный момент  . Например,
. Например, 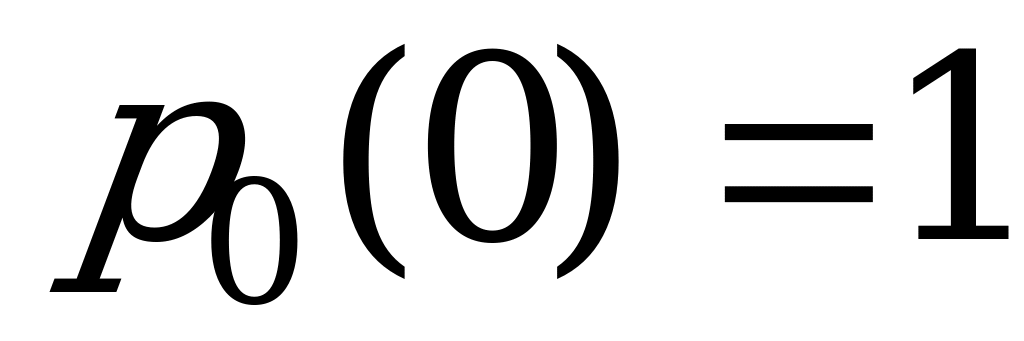 ,
, 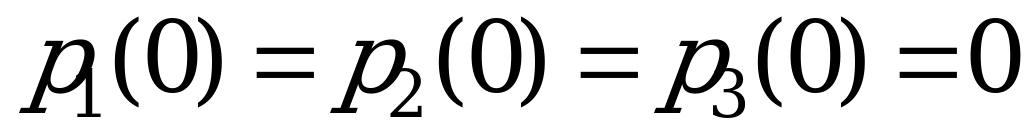 .
.
Особый интерес представляют вероятности состояний системы 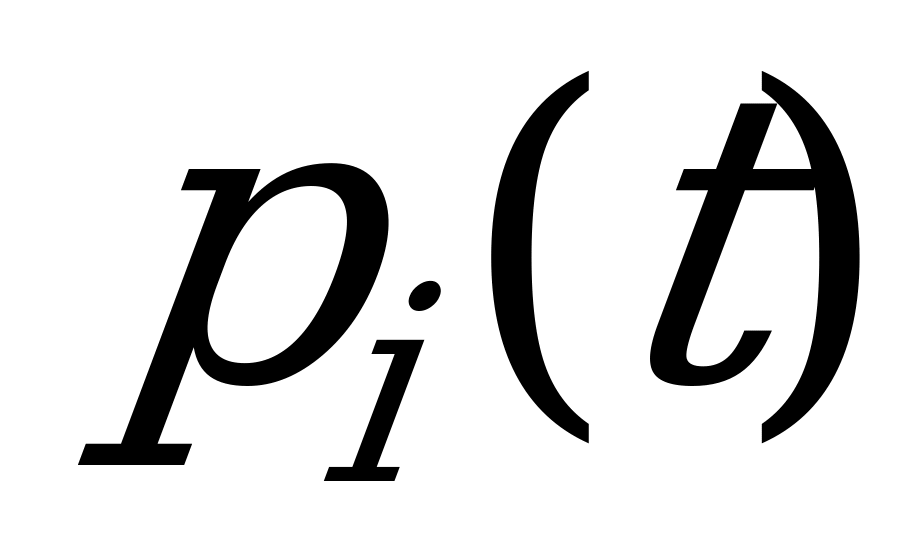 в предельном стационарном режиме, т.е. при
в предельном стационарном режиме, т.е. при  , которые называются предельными (или финальными) вероятностями состояний.
, которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то финальные вероятности существуют.
Финальная вероятность состояния имеет чёткий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если финальная вероятность состояния 
 , то это означает, что в среднем половину времени система находится в состоянии
, то это означает, что в среднем половину времени система находится в состоянии  .
.
Так как финальные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим.
Для вышеприведённого примера такая система уравнений будет иметь вид:

(Отрицательный член каждого уравнения перенесли из правой части в левую.)
Систему уравнений Колмогорова для стационарного режима можно составить, пользуясь следующим правилом: слева стоит финальная вероятность данного состояния  , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния; а справа – сумма произведений интенсивностей всех потоков, входящих в
, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния; а справа – сумма произведений интенсивностей всех потоков, входящих в 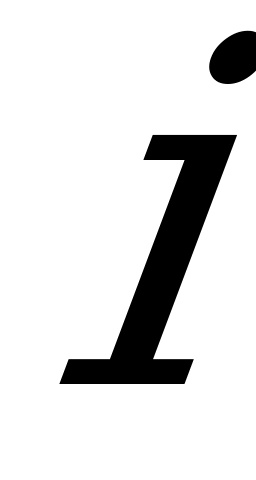 -ое состояние, на вероятности тех состояний, из которых эти потоки исходят.
-ое состояние, на вероятности тех состояний, из которых эти потоки исходят.
Получается система из  уравнений с
уравнений с  неизвестными
неизвестными 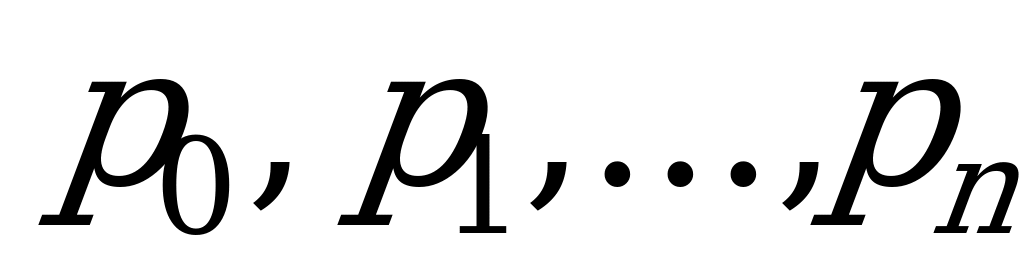 . Но эти уравнения являются однородными (не имеют свободного члена) и, значит, определяют неизвестные только с точностью до произвольного множителя. Для решения системы уравнений можно воспользоваться условием:
. Но эти уравнения являются однородными (не имеют свободного члена) и, значит, определяют неизвестные только с точностью до произвольного множителя. Для решения системы уравнений можно воспользоваться условием: 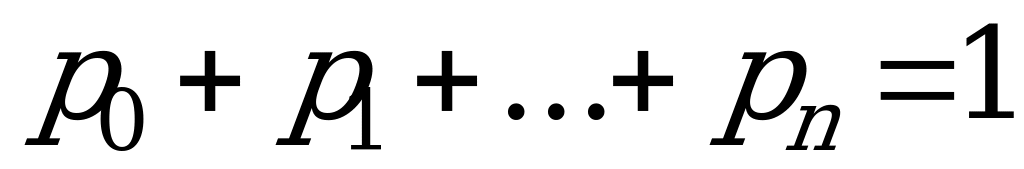 . При этом одно (любое) из уравнений системы можно отбросить.
. При этом одно (любое) из уравнений системы можно отбросить.
Простейшие системы массового обслуживания и их характеристики
Все потоки событий, переводящие СМО из состояния в состояние, считаются простейшими. В их числе и так называемый «поток обслуживаний». Под ним подразумевается поток заявок, обслуживаемых одним непрерывно занятым каналом. В этом потоке интервал между событиями (как и всегда в простейшем потоке) имеет показательное распределение, т.е. время обслуживания распределено по показательному закону.
СМО без очереди (без ожидания)
1. Одноканальная СМО (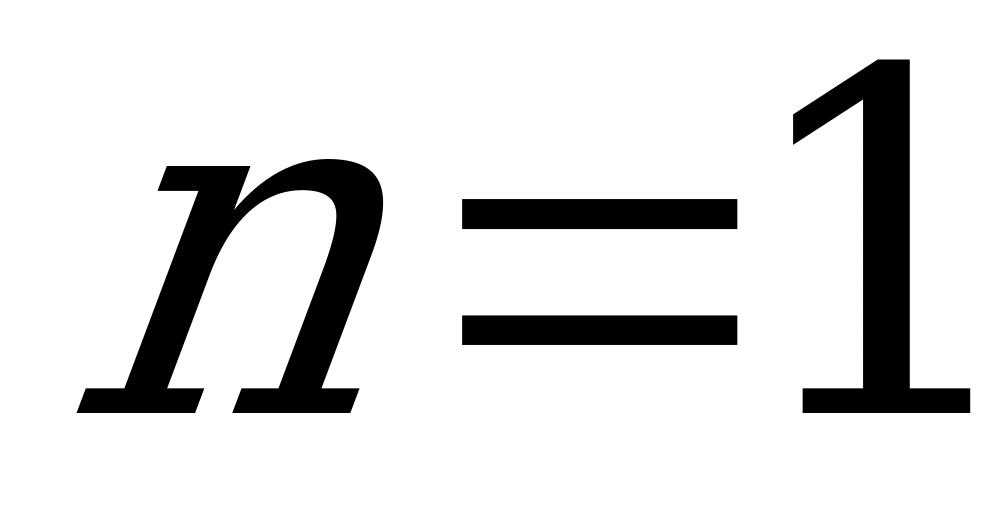 ,
, 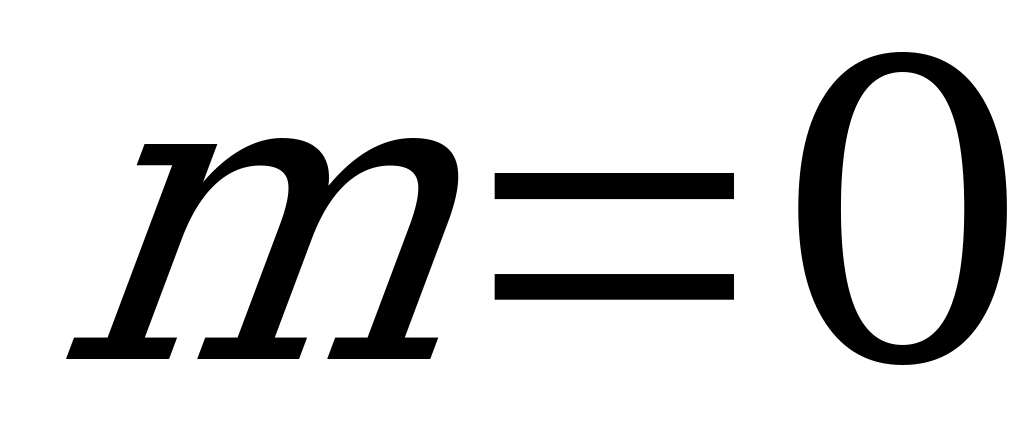 ).
).
Пусть СМО состоит только из одного ПО, и на неё поступает простейший поток заявок с интенсивностью  . Среднее время обслуживания одной заявки составляет
. Среднее время обслуживания одной заявки составляет 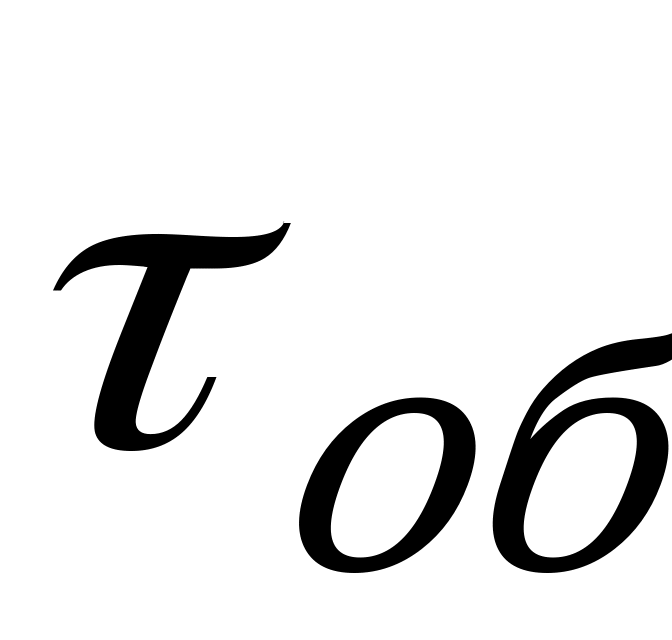 . Заявка, заставшая ПО занятым, получает отказ и покидает систему.
. Заявка, заставшая ПО занятым, получает отказ и покидает систему.



ПО





Данная СМО может находиться в двух состояниях:  - ПО свободен,
- ПО свободен,  - ПО занят.
- ПО занят.
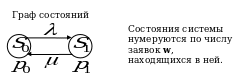
Из состояния  в
в  систему переводит входной поток заявок (как только приходит заявка, система «перескакивает» из
систему переводит входной поток заявок (как только приходит заявка, система «перескакивает» из  в
в  ). Проставляем у стрелки
). Проставляем у стрелки  интенсивность этого потока
интенсивность этого потока  . Пусть система находится в состоянии
. Пусть система находится в состоянии  (ПО занят). Он производит
(ПО занят). Он производит  обслуживаний в единицу времени (
обслуживаний в единицу времени ( ), т.е. проставляем у стрелки
), т.е. проставляем у стрелки  интенсивность
интенсивность  .
.
Система уравнений для вероятностей состояний в стационарном режиме имеет вид: 



т.е. система вырождается в одно уравнение. Учитывая условие  , можно найти финальные вероятности состояний.
, можно найти финальные вероятности состояний.
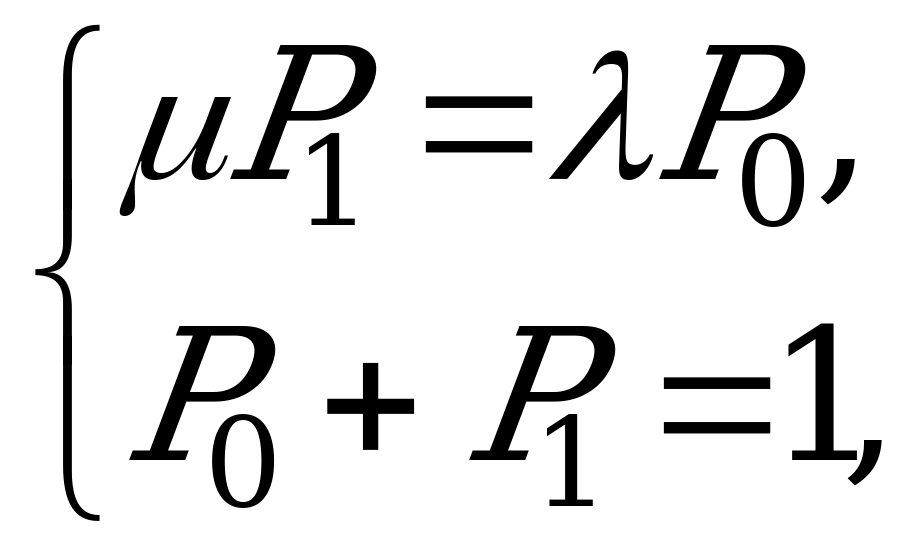

Обозначим 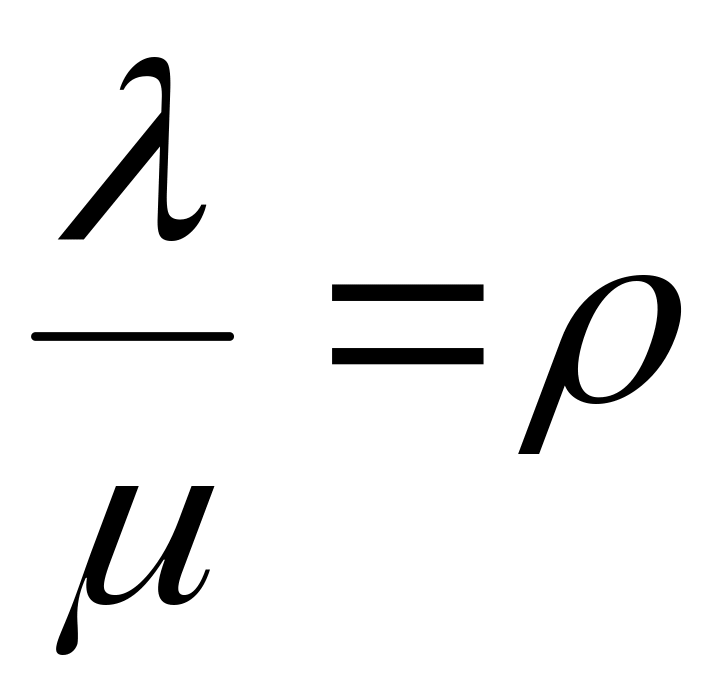 (
(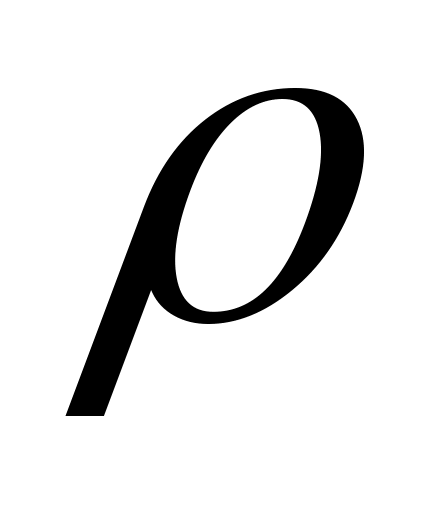 - среднее число заявок, приходящееся на среднее время обслуживания одной заявки), тогда система уравнений принимает вид:
- среднее число заявок, приходящееся на среднее время обслуживания одной заявки), тогда система уравнений принимает вид:
 откуда
откуда  ,
,  .
.
Вычислим  - вероятность того, что пришедшая заявка получит отказ (не будет обслужена):
- вероятность того, что пришедшая заявка получит отказ (не будет обслужена):  .
.
Относительная пропускная способность  - средняя доля заявок, обслуженных системой (вероятность того, что заявка будет обслужена):
- средняя доля заявок, обслуженных системой (вероятность того, что заявка будет обслужена): 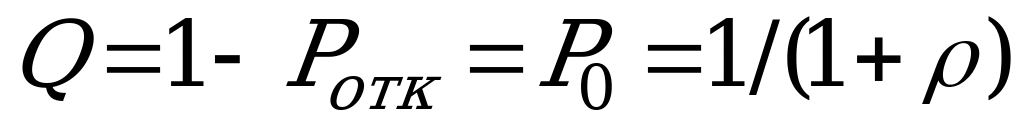 .
.
Абсолютная пропускная способность  - среднее количество заявок, обслуживаемых в единицу времени (интенсивность потока обслуженных системой заявок):
- среднее количество заявок, обслуживаемых в единицу времени (интенсивность потока обслуженных системой заявок):
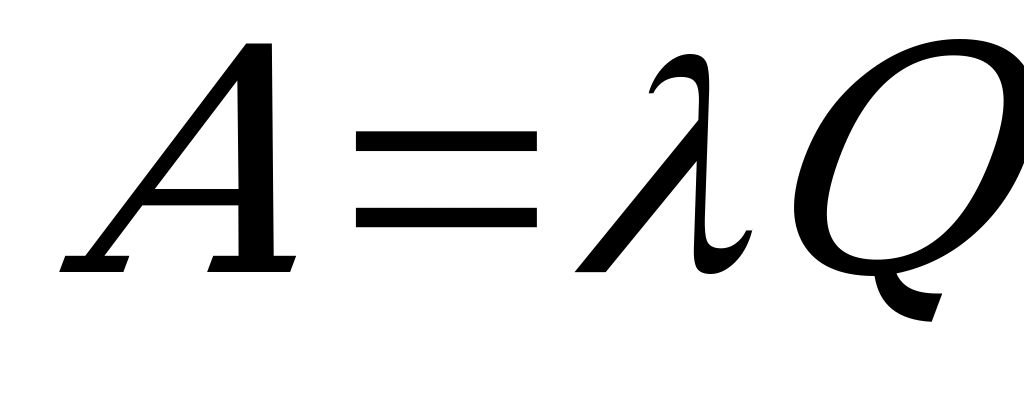 .
.
Интенсивность потока отказов  .
.
Среднее число занятых ПО  есть математическое ожидание числа занятых ПО:
есть математическое ожидание числа занятых ПО:
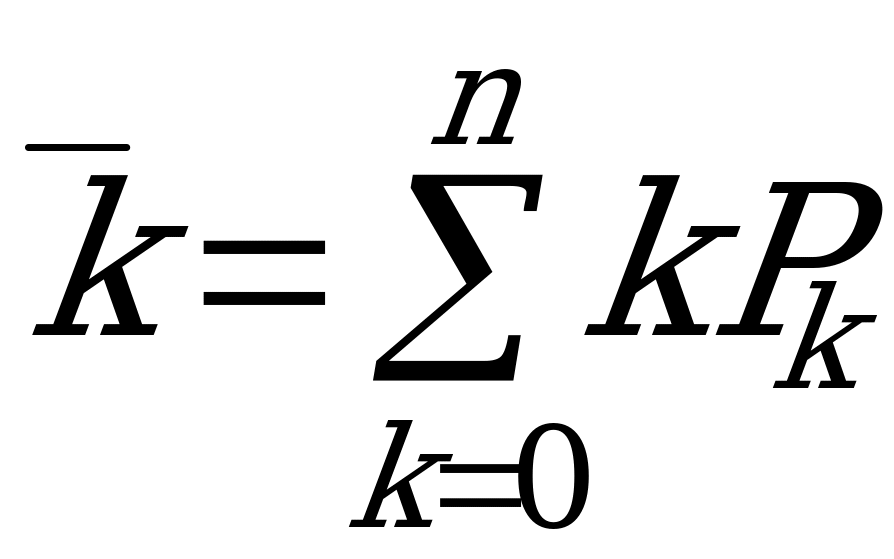 , где
, где  - финальные вероятности состояний.
- финальные вероятности состояний.

Среднее число занятых ПО можно найти, если учесть, что абсолютная пропускная способность

есть интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый прибор обслуживает в среднем

заявок (в единицу времени), то

.
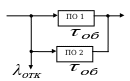

2. Двухканальная СМО ( ,
, 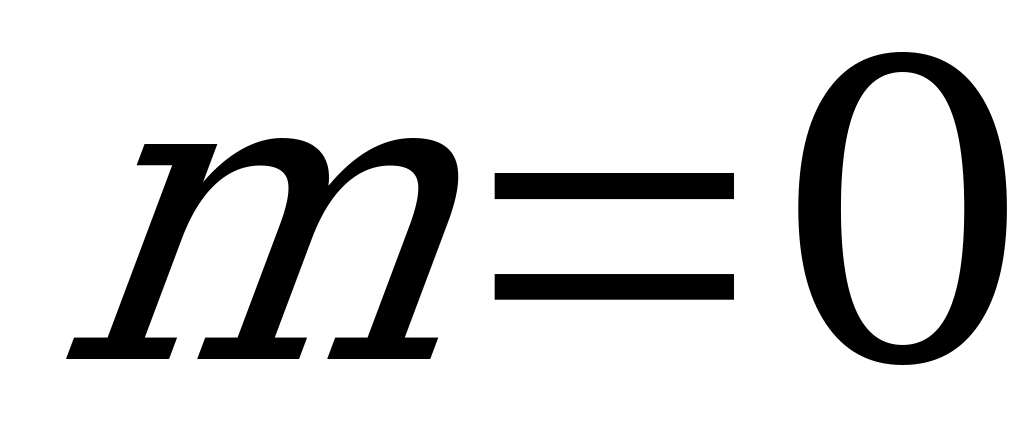 ).
).
Считается, что ПО1 и ПО2 одинаковые;
заявка занимает любой свободный прибор;
если оба прибора свободны, заявка занимает ПО1.
В озможные состояния системы:
озможные состояния системы:
 - оба ПО свободны,
- оба ПО свободны,
 - один ПО занят,
- один ПО занят,
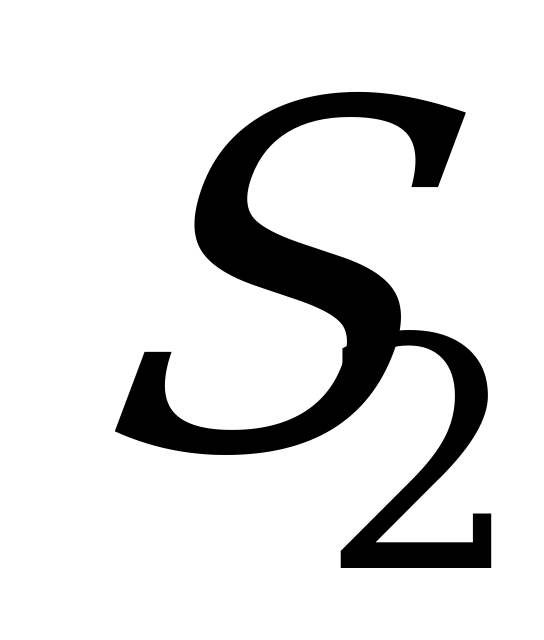 - оба ПО заняты.
- оба ПО заняты.
Из состояния  в
в  систему переводит поток заявок с интенсивностью
систему переводит поток заявок с интенсивностью  . Тот же поток заявок переводит систему из состояния
. Тот же поток заявок переводит систему из состояния  в
в 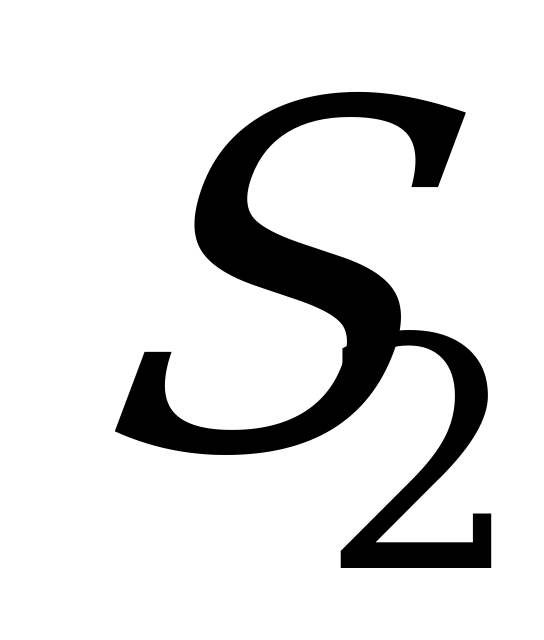 .
.
Проставим интенсивности у нижних стрелок. Пусть система находится в состоянии  (занят один ПО). Он обслуживает
(занят один ПО). Он обслуживает  заявок в единицу времени. Проставляем у стрелки
заявок в единицу времени. Проставляем у стрелки  интенсивность
интенсивность  . Теперь представим себе, что система находится в состоянии
. Теперь представим себе, что система находится в состоянии 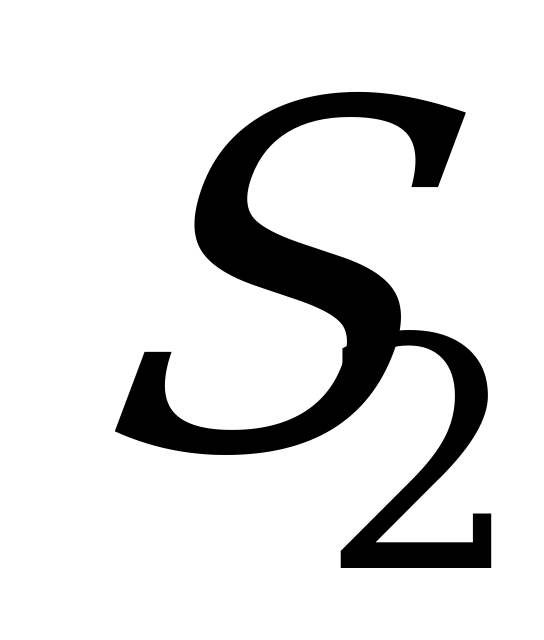 (заняты оба ПО). Для перехода системы в состояние
(заняты оба ПО). Для перехода системы в состояние  нужно, чтобы либо закончил обслуживание первый ПО, либо второй ПО.
нужно, чтобы либо закончил обслуживание первый ПО, либо второй ПО.
Вероятность перехода  в течение времени
в течение времени 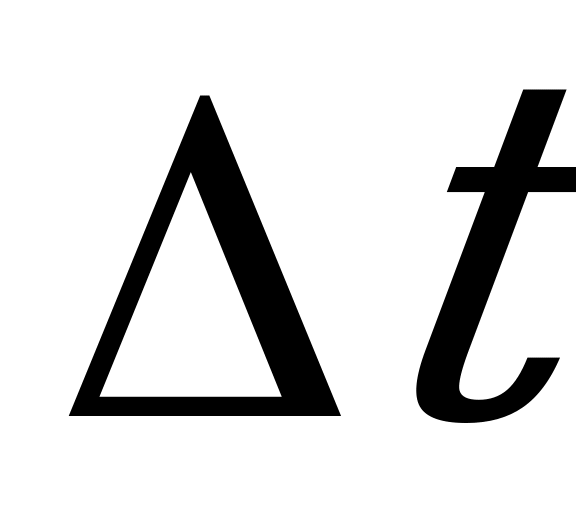 равна:
равна:
 (осв. ПО1 или осв. ПО2).
(осв. ПО1 или осв. ПО2).
Вероятность суммы событий, т.е. того, что произойдёт или событие  , или событие
, или событие 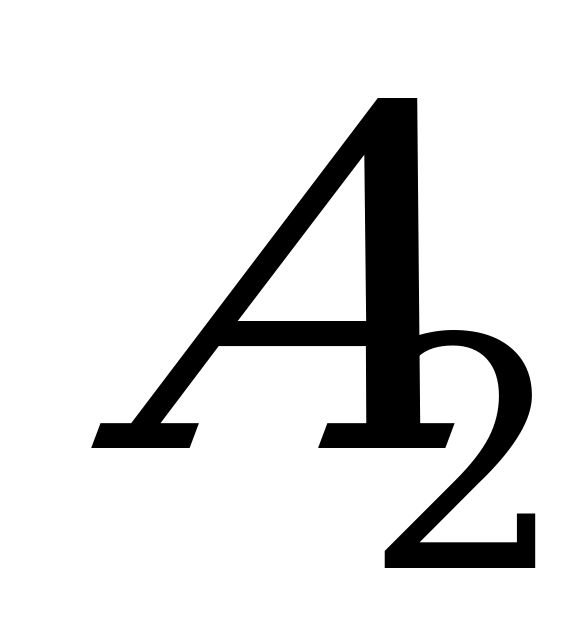 , равна:
, равна: 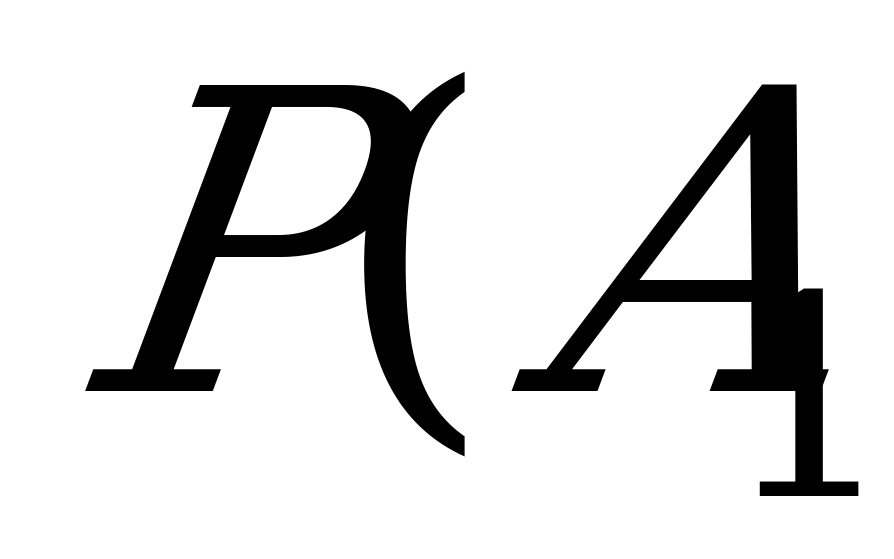 или
или  .
.
Следовательно,
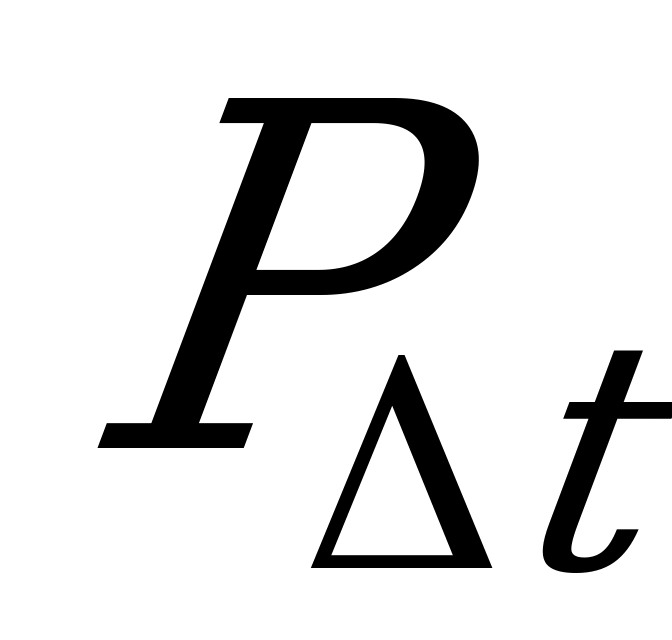 (осв. ПО1 или осв. ПО2)
(осв. ПО1 или осв. ПО2)  (осв. ПО1)
(осв. ПО1) (осв. ПО2)
(осв. ПО2)  .
.
(Вероятность освобождения ПО в течение времени 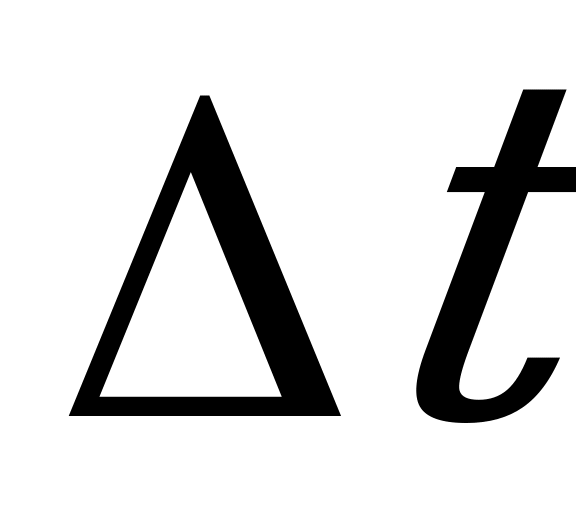 равна интенсивности потока обслу-живаний, умноженной на промежуток времени
равна интенсивности потока обслу-живаний, умноженной на промежуток времени 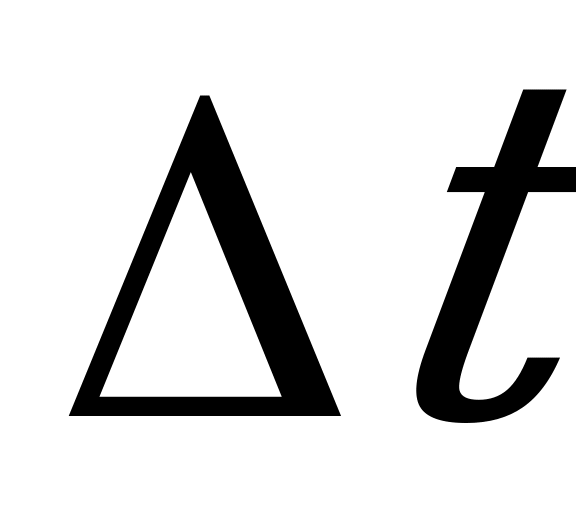 :
: 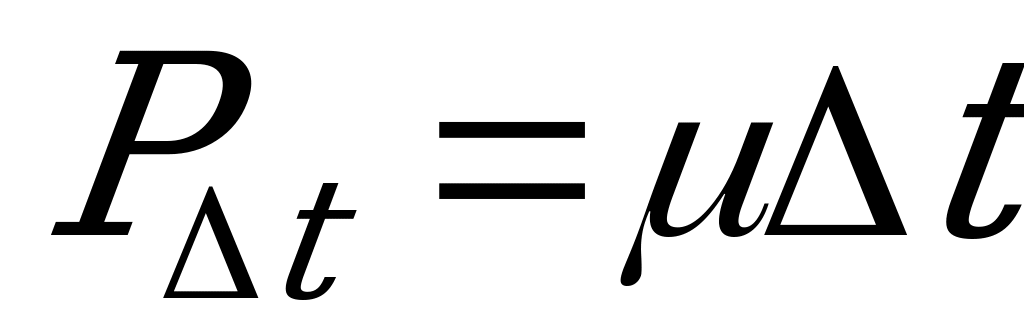 ).
).
Таким образом, интенсивность перехода  равна
равна 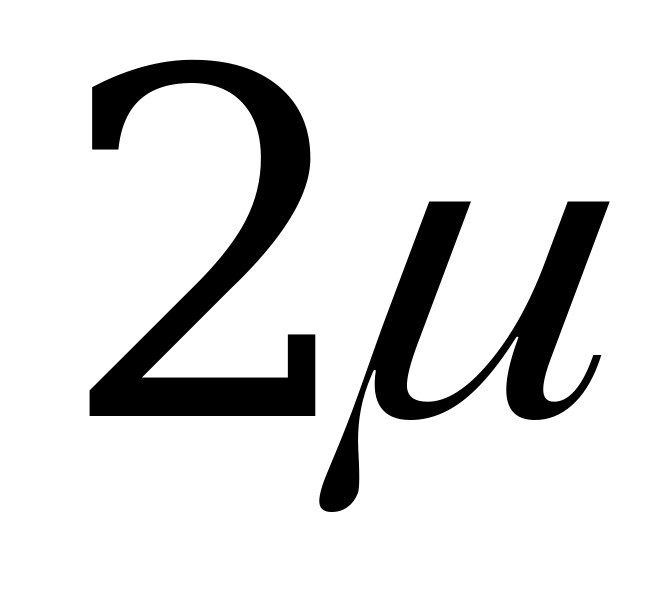 .
.
Переходы  и
и  запрещены, т.к. в каждый момент времени может произойти только одно событие (поток событий - ординарный): исключено одновременное появление двух заявок, а также одновременное освобождение двух приборов.
запрещены, т.к. в каждый момент времени может произойти только одно событие (поток событий - ординарный): исключено одновременное появление двух заявок, а также одновременное освобождение двух приборов.
Система уравнений: 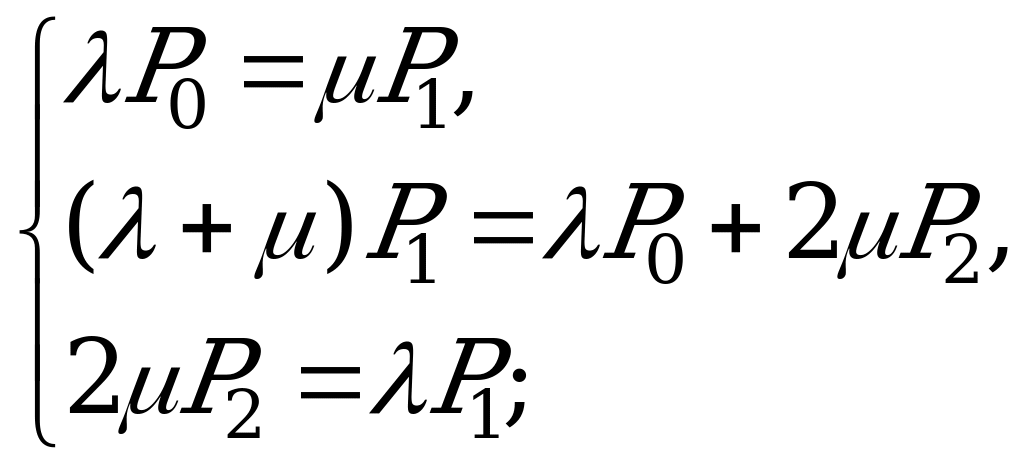
 .
.
Финальные вероятности:  ;
;  ;
;  .
.
Вероятность того, что пришедшая заявка получит отказ: 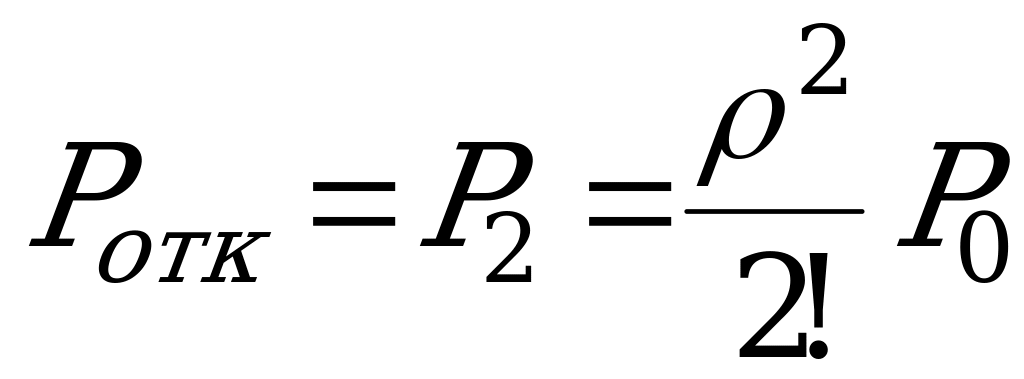 .
.


Относительная Абсолютная Среднее число
пропускная пропускная занятых
способность: способность: приборов:
 .
. 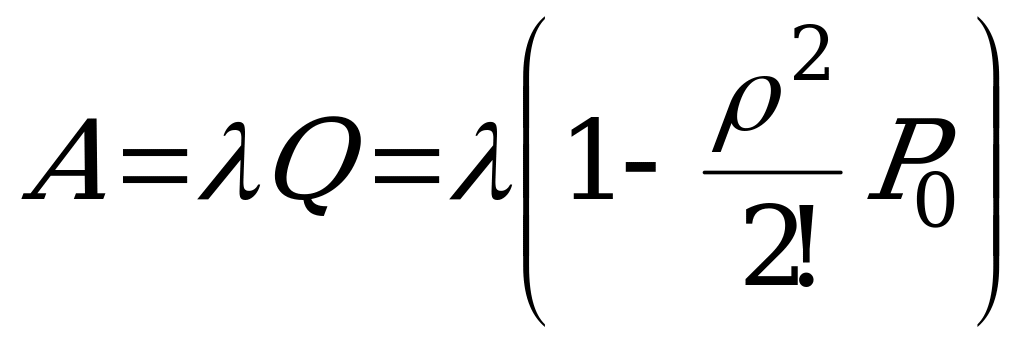 .
. 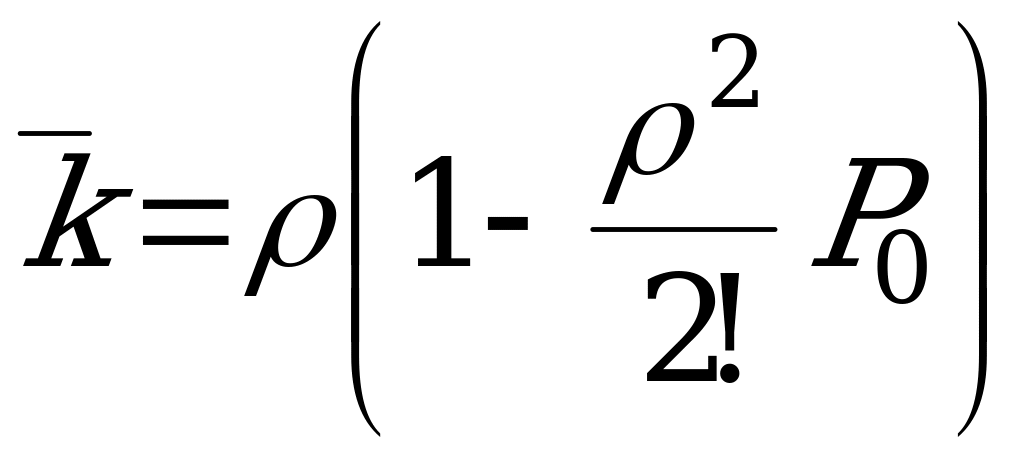 .
.
3. Многоканальная СМО (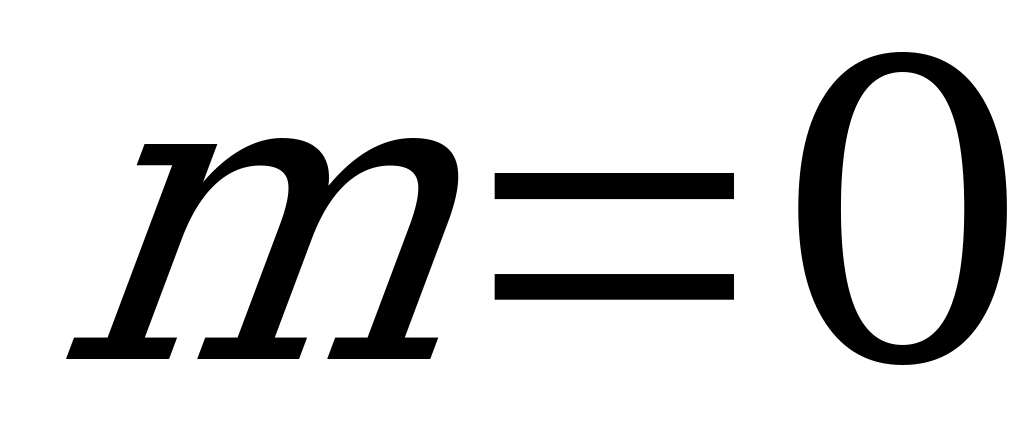 ).
).
Имеется  ПО, на которые поступает поток заявок с интенсивностью
ПО, на которые поступает поток заявок с интенсивностью  . Поток обслуживаний имеет интенсивность
. Поток обслуживаний имеет интенсивность  .
.
Возможные состояния системы:
 - все приборы свободны (в СМО нет ни одной заявки);
- все приборы свободны (в СМО нет ни одной заявки);
 - один ПО занят, остальные свободны;
- один ПО занят, остальные свободны;
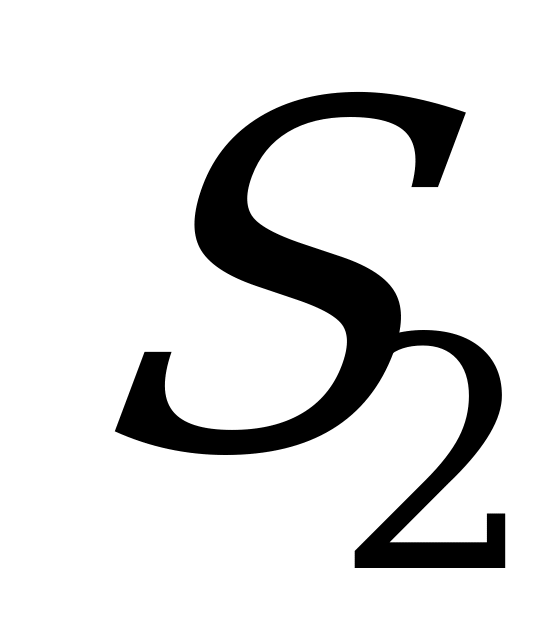 - заняты два ПО;
- заняты два ПО;
……………………..
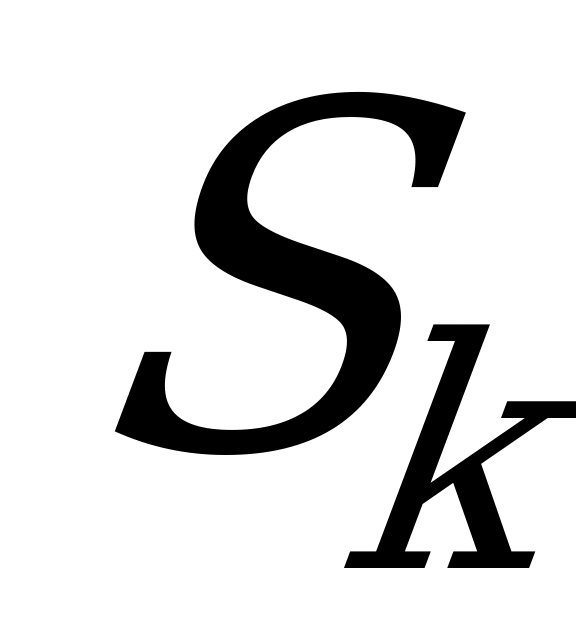 - заняты
- заняты  ПО (в СМО находится
ПО (в СМО находится  заявок);
заявок);
……………………..
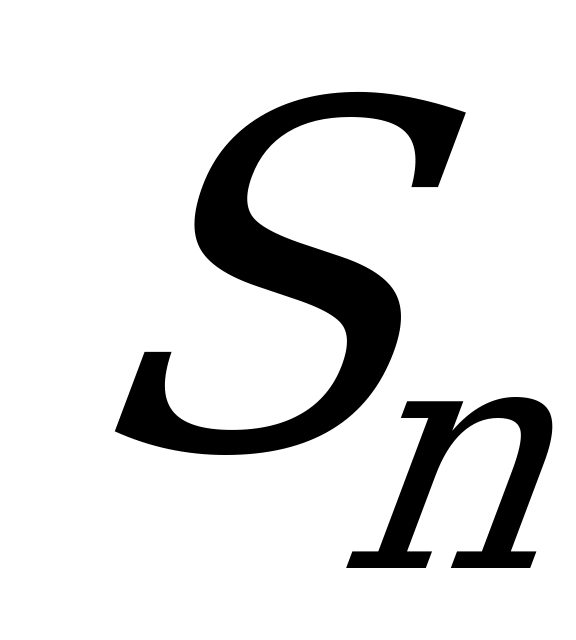
 - все
- все  ПО заняты (в СМО находится
ПО заняты (в СМО находится  заявок).
заявок).
Финальные вероятности состояний: 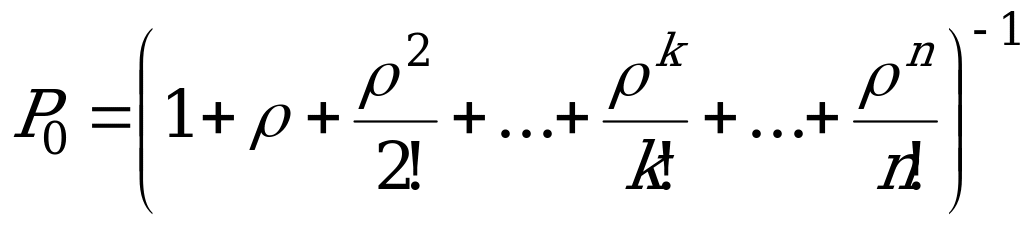
(скобку возводят в степень -1, чтобы не писать двухэтажных дробей),
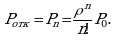
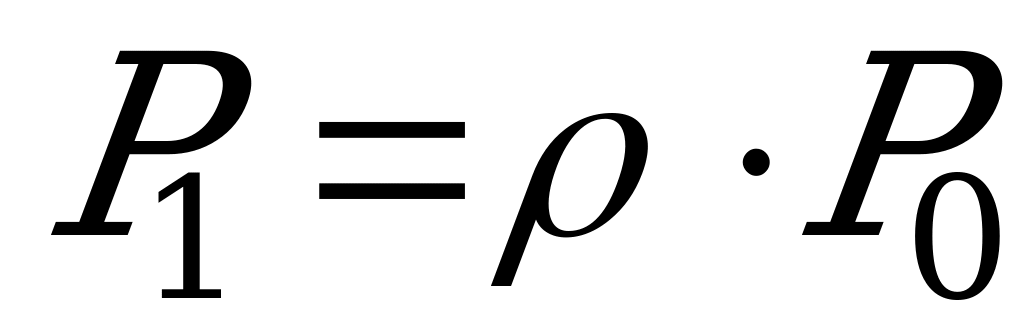 ,
,  , …
, …  , …
, … 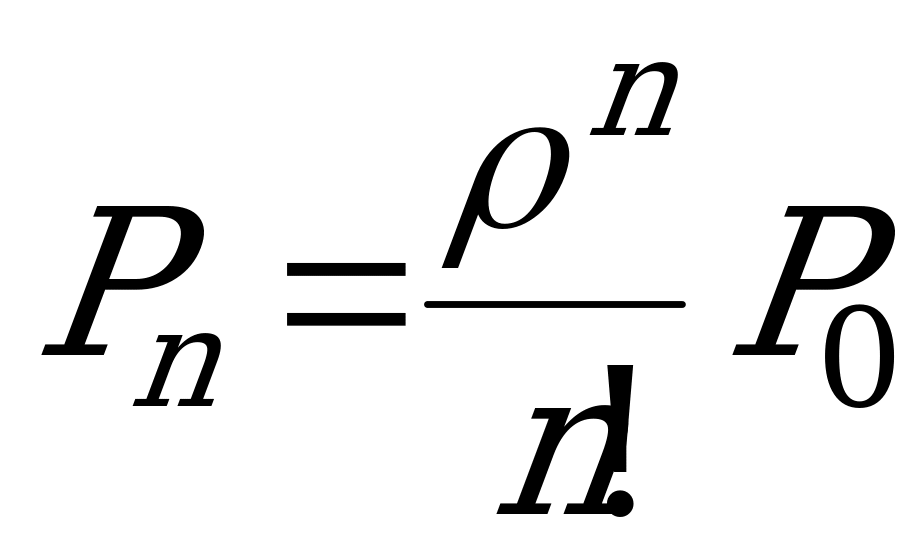 .
.
Вероятность того, что пришедшая заявка получит отказ (для этого нужно, чтобы все  ПО были заняты):
ПО были заняты):


Относительная Абсолютная Среднее число
пропускная пропускная занятых
способность: способность: приборов:
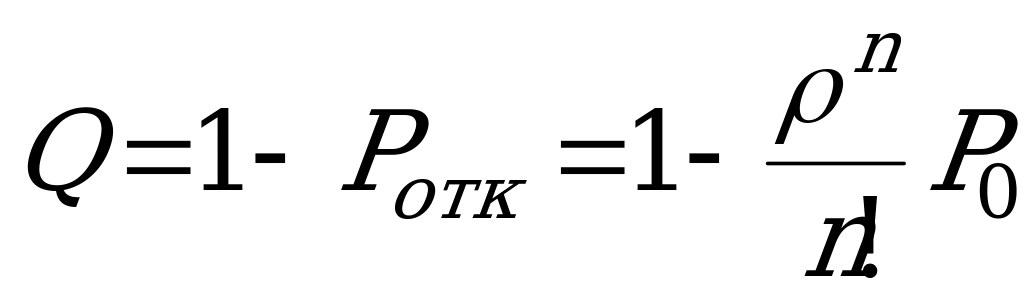 .
.  .
.  .
.
СМО с ожиданием (с очередью)
В качестве показателей эффективности СМО с очередью, кроме уже известных, рассматривают также  - среднее число заявок в системе,
- среднее число заявок в системе,  - среднее время пребывания заявки в системе,
- среднее время пребывания заявки в системе,  - среднее число заявок в очереди (длина очереди),
- среднее число заявок в очереди (длина очереди),  - среднее время пребывания заявки в очереди,
- среднее время пребывания заявки в очереди,  - вероятность того, что прибор обслуживания занят (степень загрузки канала).
- вероятность того, что прибор обслуживания занят (степень загрузки канала).
1. Одноканальная СМО с очередью  .
.
Если число заявок в очереди равно  , то следующая заявка в очередь не становится, а покидает систему необслуженной.
, то следующая заявка в очередь не становится, а покидает систему необслуженной.
 Возможные состояния системы:
Возможные состояния системы:
 - ПО свободен;
- ПО свободен;
 - ПО занят (обслуживает заявку), очереди нет (
- ПО занят (обслуживает заявку), очереди нет ( );
);
 - ПО занят, одна заявка стоит в очереди (
- ПО занят, одна заявка стоит в очереди ( ).
).
Система уравнений:
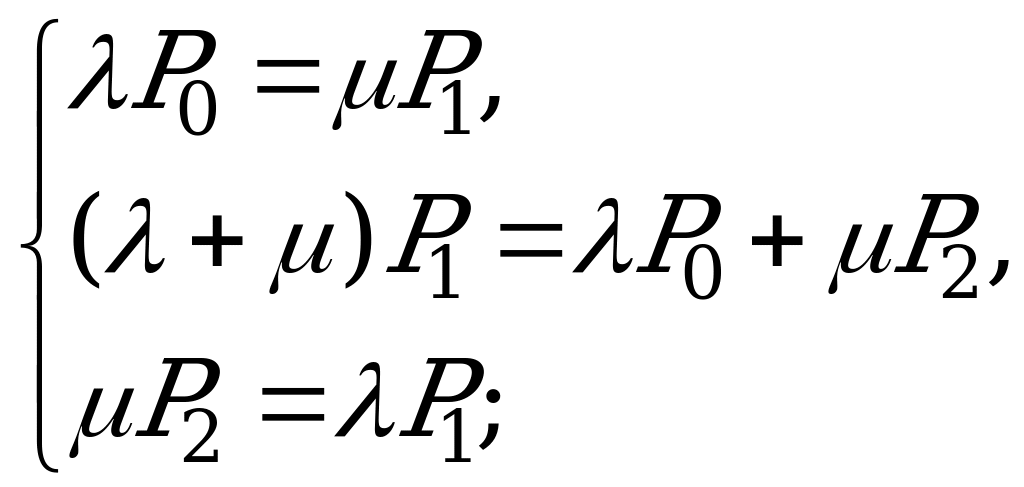
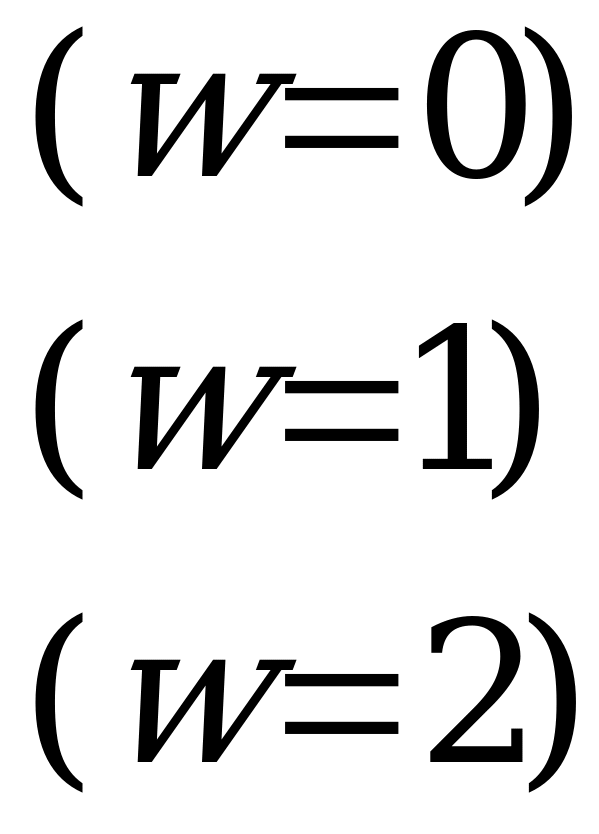
 (
( - число заявок в СМО).
- число заявок в СМО).
Финальные вероятности: 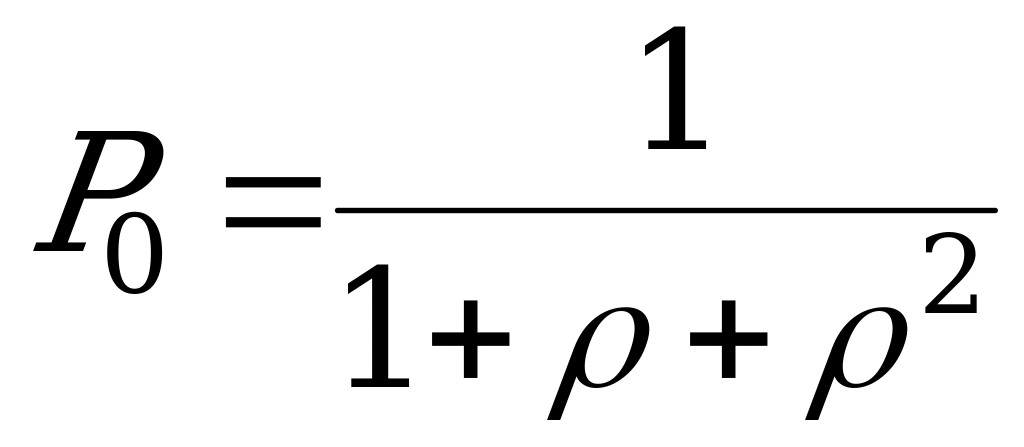 ;
; 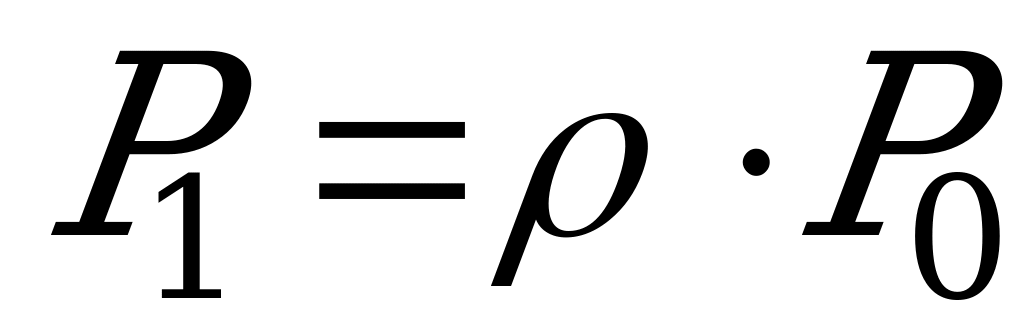 ;
;  .
.

Вероятность того, что пришедшая заявка получит отказ (если система находится в состоянии

):
Относительная пропускная способность:

. Абсолютная пропускная способность:

.
Вероятность того, что ПО занят:  .
.
Среднее число заявок под обслуживанием (среднее число занятых приборов):
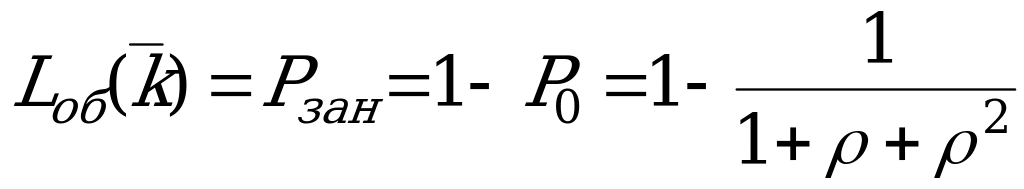 .
.
Среднее число заявок в СМО: 
(случайная величина  - число заявок в системе – имеет возможные значения 0, 1, 2 с вероятностями
- число заявок в системе – имеет возможные значения 0, 1, 2 с вероятностями 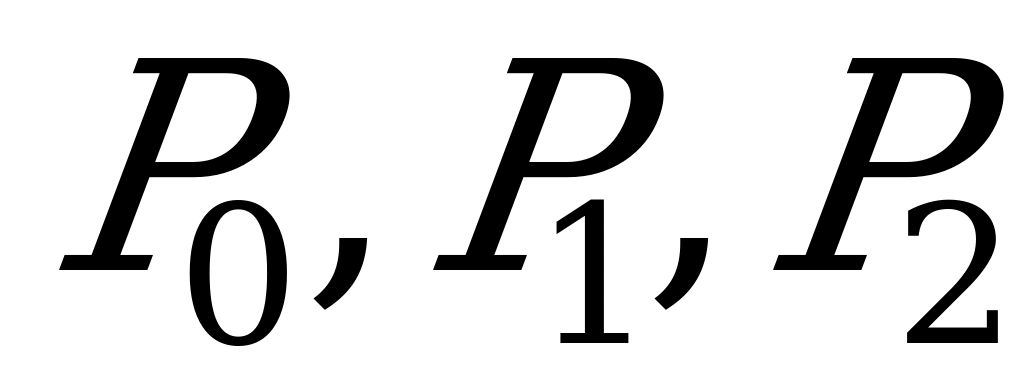 ;
;  - математическое ожидание
- математическое ожидание  ).
).
Среднее число заявок в очереди:  .
.
Среднее время пребывания заявки в СМО:

Среднее время пребывания заявки в очереди:
Последние две формулы называются формулами Литтла.
2. Одноканальная СМО с очередью 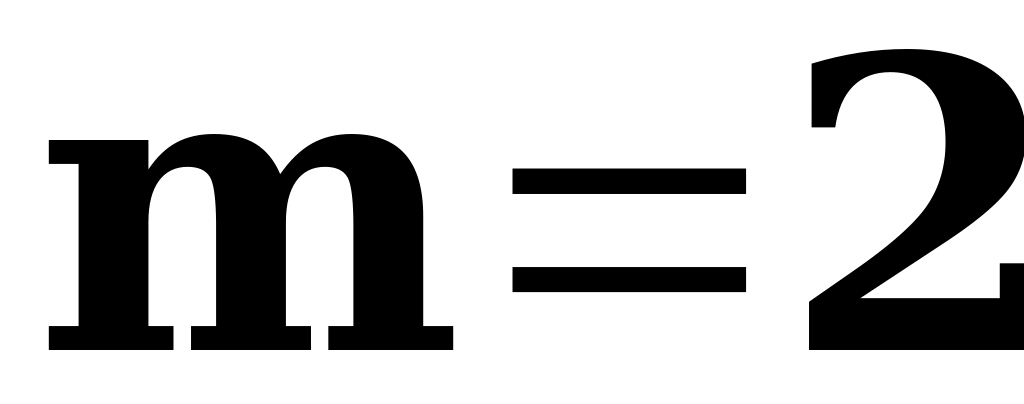 .
.
Возможные состояния системы:
 - ПО свободен;
- ПО свободен;
 - ПО занят (обслуживает заявку), очереди нет (
- ПО занят (обслуживает заявку), очереди нет ( );
);
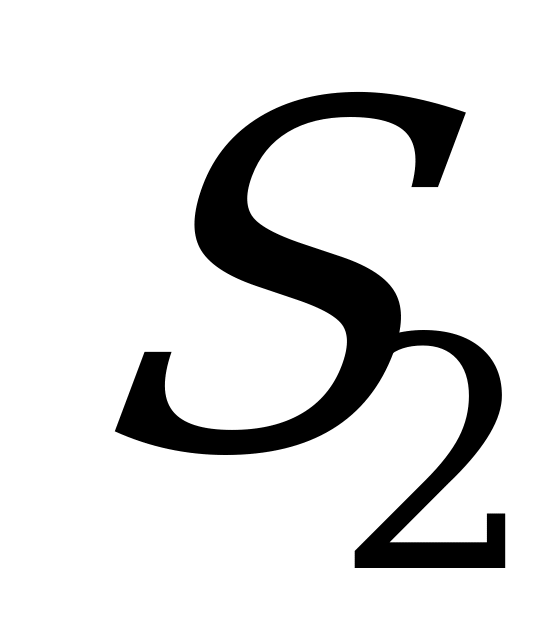 - ПО занят, одна заявка стоит в очереди (
- ПО занят, одна заявка стоит в очереди ( );
);
 - ПО занят, две заявки стоят в очереди (
- ПО занят, две заявки стоят в очереди ( ).
).
С
Граф состояний
истема уравнений:


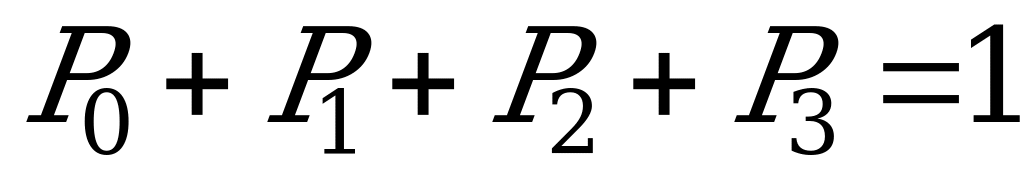 .
.
Финальные вероятности:  ;
; 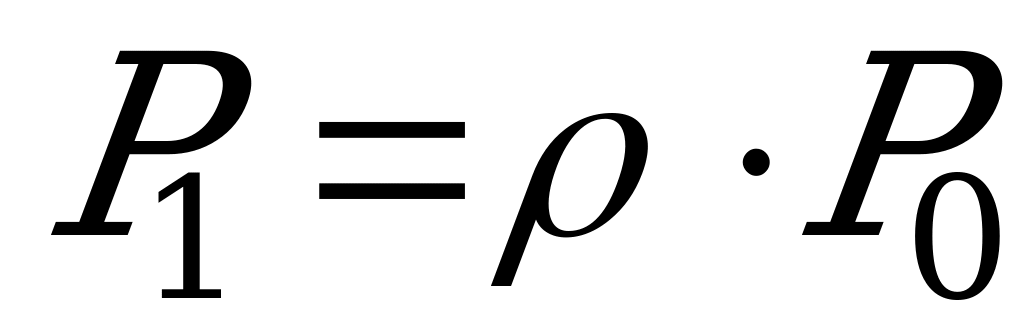 ;
;  ;
;  .
.
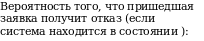

Относительная пропускная способность:  .
.
Абсолютная пропускная способность:  .
.
Вероятность того, что ПО занят: 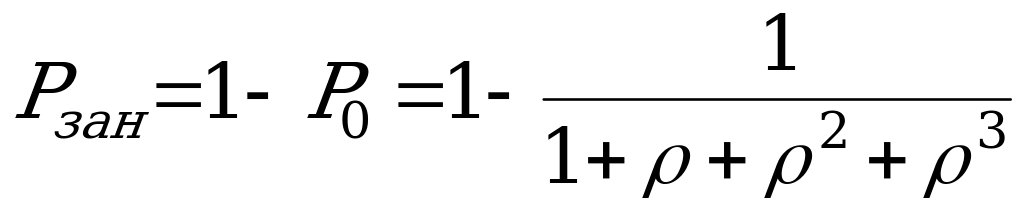 .
.
Среднее число заявок под обслуживанием (среднее число занятых приборов):

Среднее число заявок в СМО: 
(случайная величина  - число заявок в системе – имеет возможные значения 0, 1, 2, 3 с вероятностями
- число заявок в системе – имеет возможные значения 0, 1, 2, 3 с вероятностями  ;
; 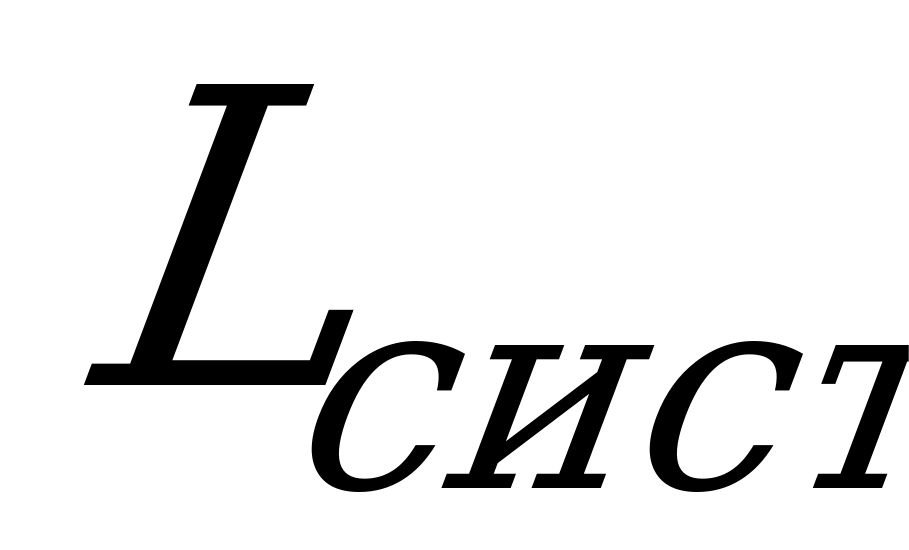 - математическое ожидание
- математическое ожидание  ).
).
Среднее число заявок в очереди:  .
.
Среднее время пребывания заявки в СМО: 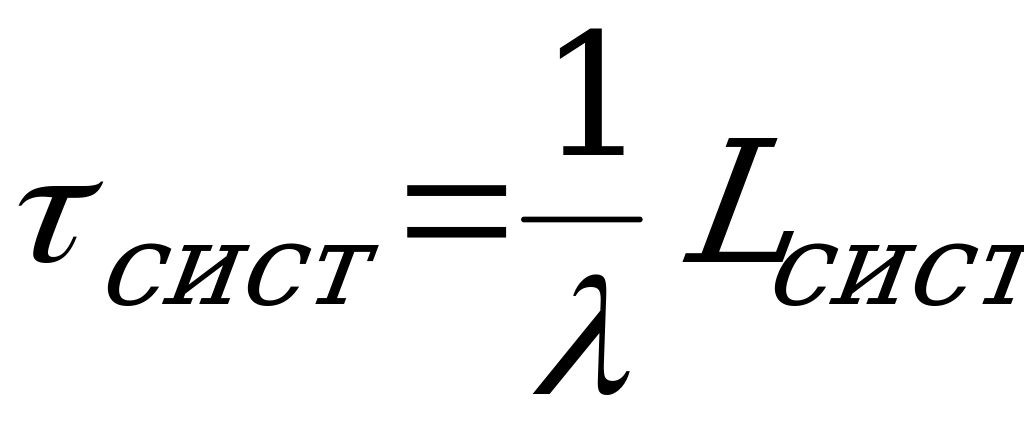 .
.
Среднее время пребывания заявки в очереди:  .
.
3. Одноканальная СМО с неограниченной очередью.
Возможные состояния системы:
 - ПО свободен;
- ПО свободен;
 - ПО занят (обслуживает заявку), очереди нет (
- ПО занят (обслуживает заявку), очереди нет ( );
);
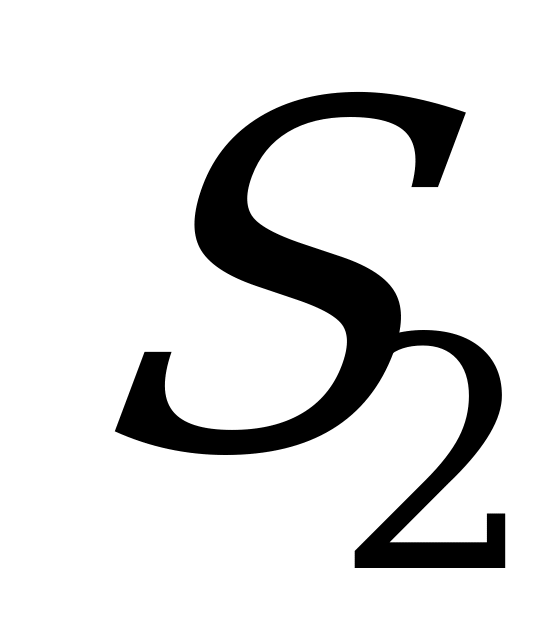 - ПО занят, одна заявка стоит в очереди (
- ПО занят, одна заявка стоит в очереди ( );
);
 - ПО занят, две заявки стоят в очереди (
- ПО занят, две заявки стоят в очереди ( );
);
… … … … … … … … … … … … … … … … …
 - ПО занят,
- ПО занят,  ;
;
… … … … … … … … … … … … … … … … … .
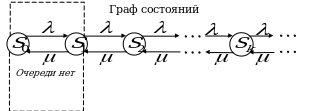
Теоретически число состояний системы ничем не ограничено (бесконечно). По всем стрелкам поток заявок с интенсивностью  переводит систему слева направо, а справа налево – поток обслуживаний с интенсивностью
переводит систему слева направо, а справа налево – поток обслуживаний с интенсивностью  .
.
Финальные вероятности для такой СМО существуют только тогда, когда система не перегружена (при  ). Если
). Если  , то очередь при
, то очередь при  растёт неограниченно.
растёт неограниченно.
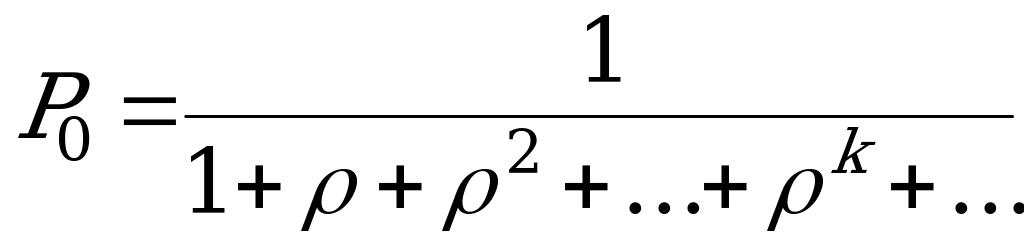
Ряд в этой формуле представляет собой геометрическую прогрессию. При  ряд сходится – это бесконечно убывающая геометрическая прогрессия со знаменателем
ряд сходится – это бесконечно убывающая геометрическая прогрессия со знаменателем 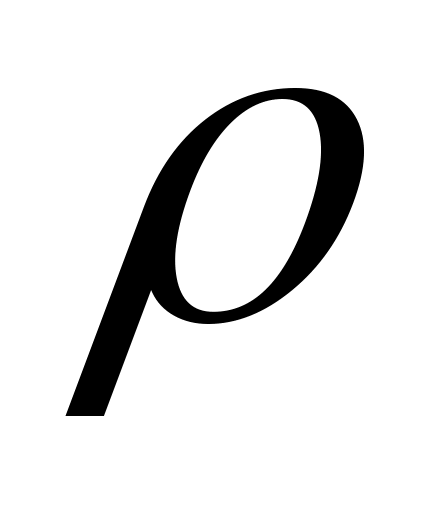 .
.
Суммируя прогрессию, имеем: 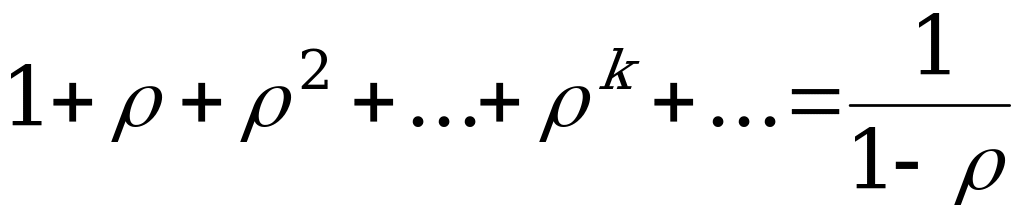 , откуда
, откуда  .
.
Вероятности  находятся по формулам:
находятся по формулам:
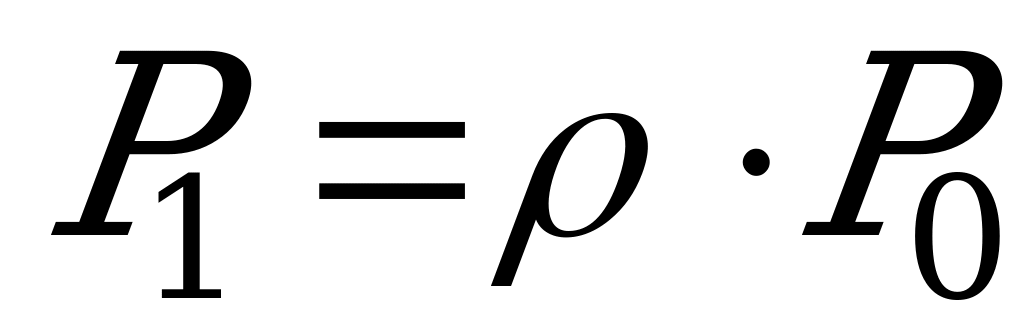 ,
,  , …,
, …,  , …,
, …,
или  ,
,  , …,
, …,  , … .
, … .
Относительная пропускная способность: 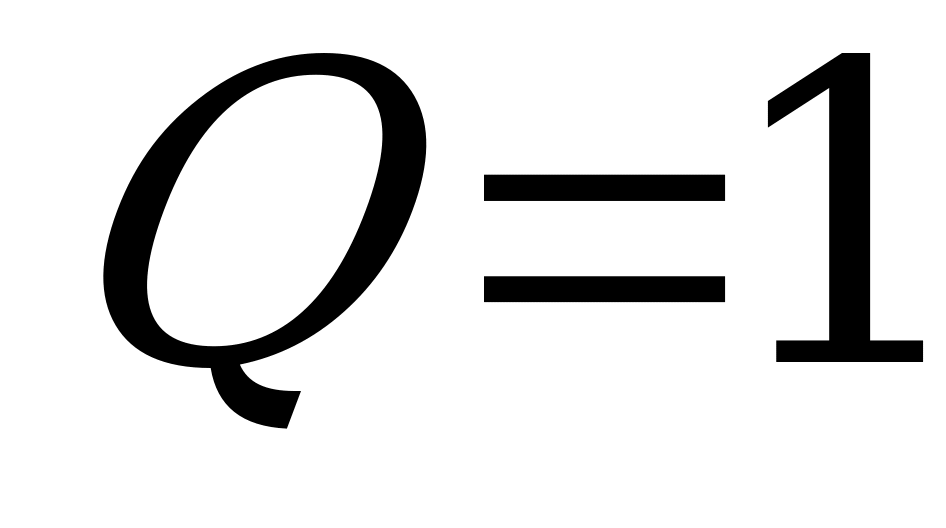 (в силу того, что очередь не ограничена, каждая заявка рано или поздно будет обслужена).
(в силу того, что очередь не ограничена, каждая заявка рано или поздно будет обслужена).
Абсолютная пропускная способность: 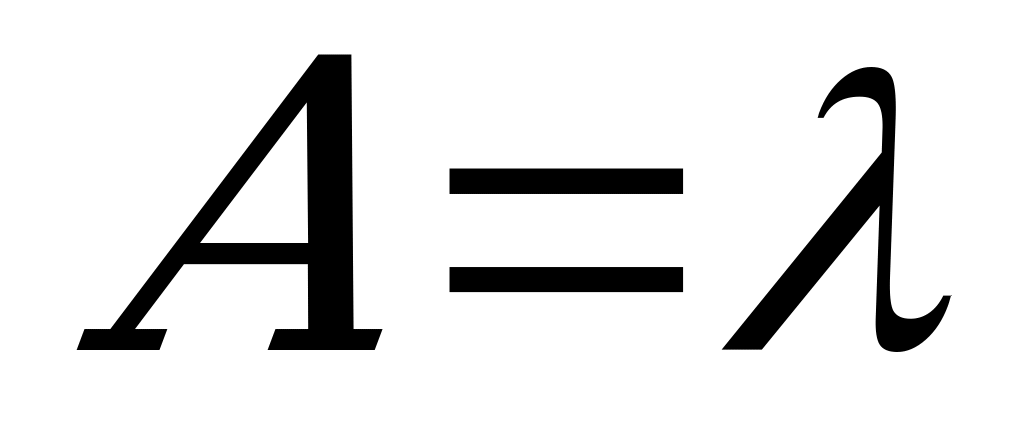 .
.
Среднее число заявок в СМО:  .
.
Среднее время пребывания заявки в СМО: 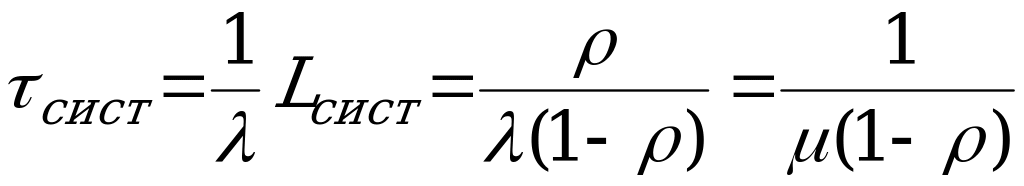 .
.
Вероятность того, что ПО занят:  .
.
Среднее число заявок под обслуживанием: 
Среднее число заявок в очереди:  .
.
Среднее время пребывания заявки в очереди:  .
.
4. Многоканальная СМО с неограниченной очередью.
Возможные состояния системы:
 - все ПО свободны;
- все ПО свободны;
 - один ПО занят, остальные свободны;
- один ПО занят, остальные свободны;
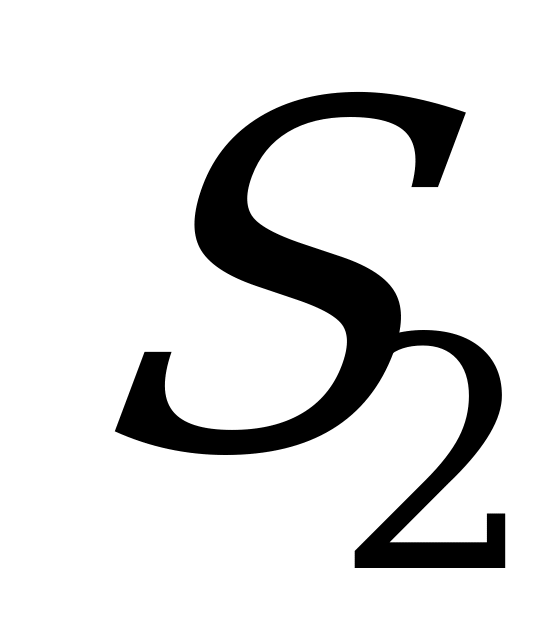 - заняты два ПО, остальные свободны;
- заняты два ПО, остальные свободны;
… … … … … … … … … … … … … … … … …
 - заняты
- заняты  ПО, остальные свободны;
ПО, остальные свободны;
… … … … … … … … … … … … … … … … …
 - заняты все ПО, очереди нет
- заняты все ПО, очереди нет 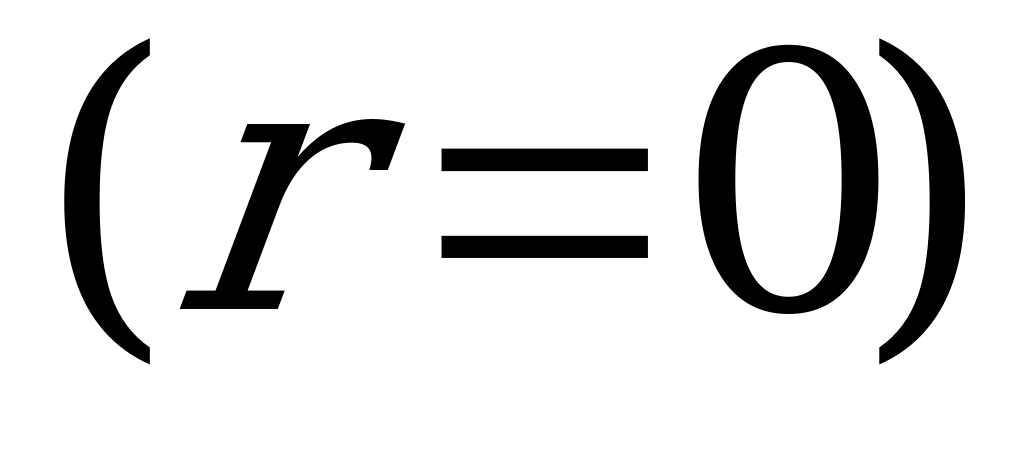 ;
;
 - заняты все ПО, одна заявка стоит в очереди
- заняты все ПО, одна заявка стоит в очереди  ;
;
… … … … … … … … … … … … … … … … …
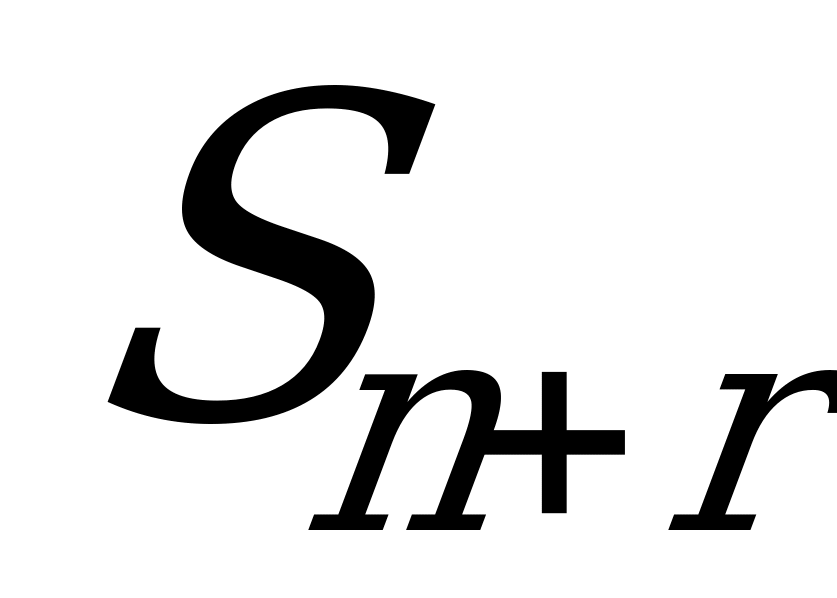
 - заняты все ПО,
- заняты все ПО,  заявок стоит в очереди;
заявок стоит в очереди;
…
Граф состояний
… … … … … … … … … … … … … … … … .
Финальные вероятности (существуют при 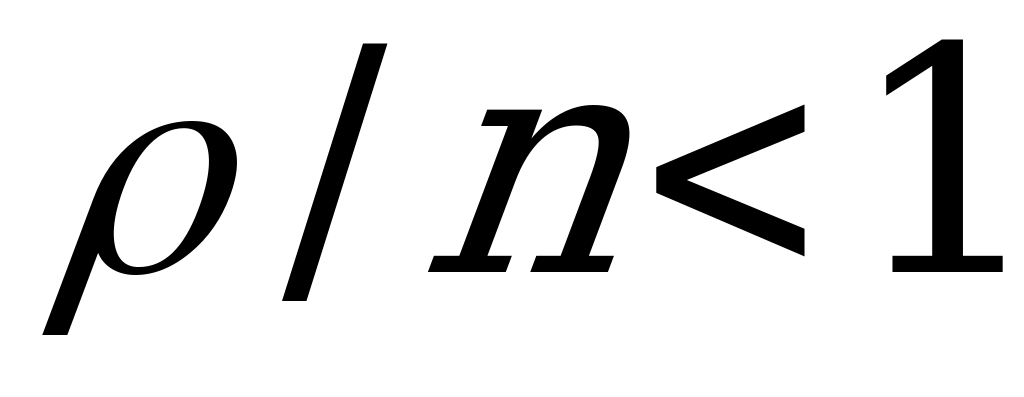 ):
):
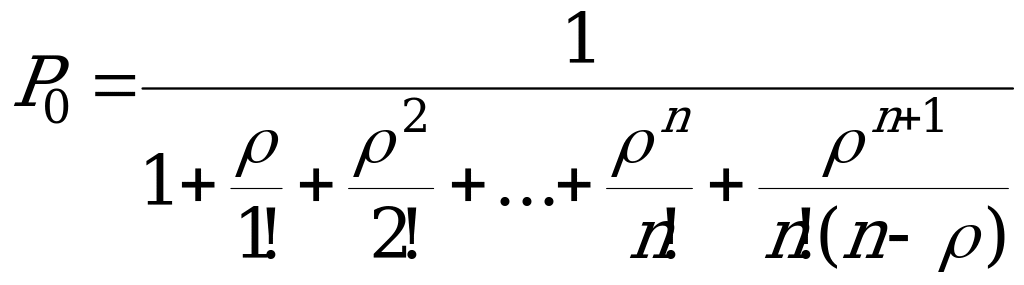 ;
;
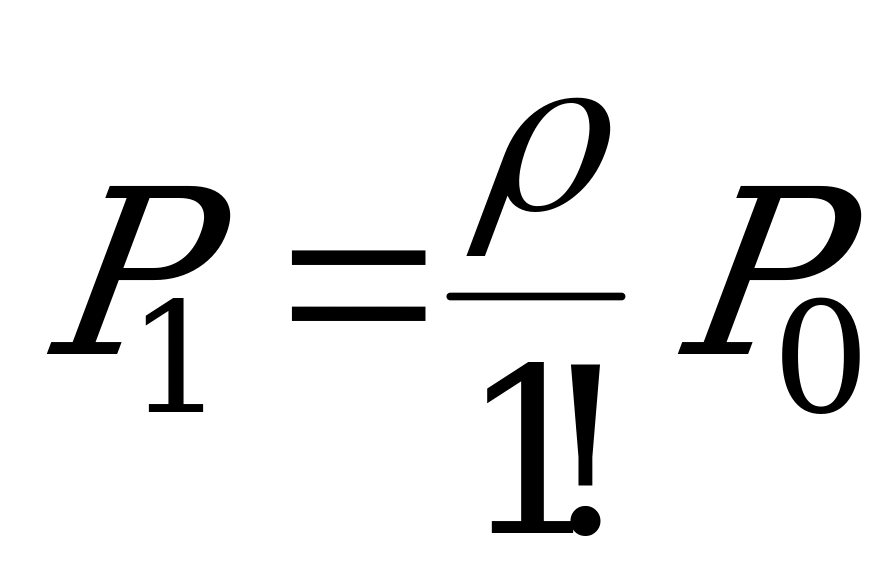 ,
,  , …,
, …,  , …,
, …, 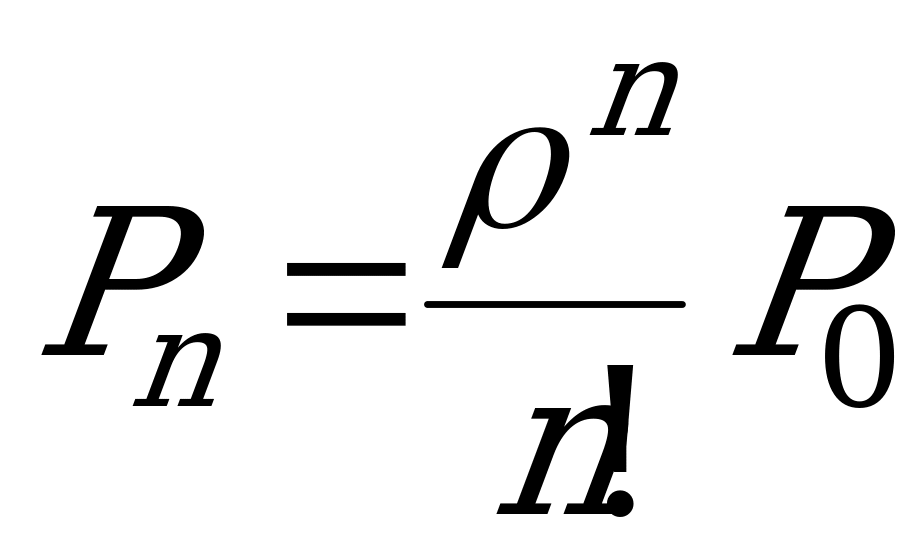 ,
,
 , …,
, …,  , … .
, … .
Относительная пропускная способность: 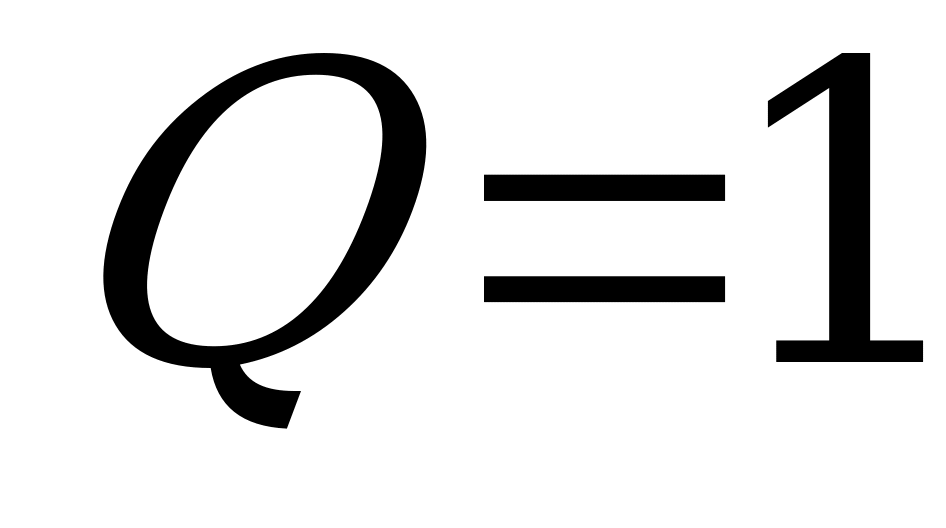 .
.
Абсолютная пропускная способность: 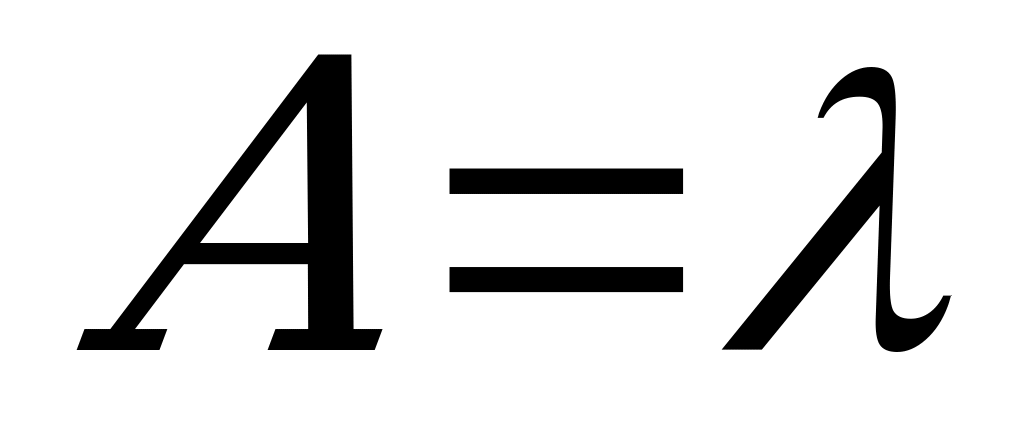 .
.
Среднее число занятых ПО: 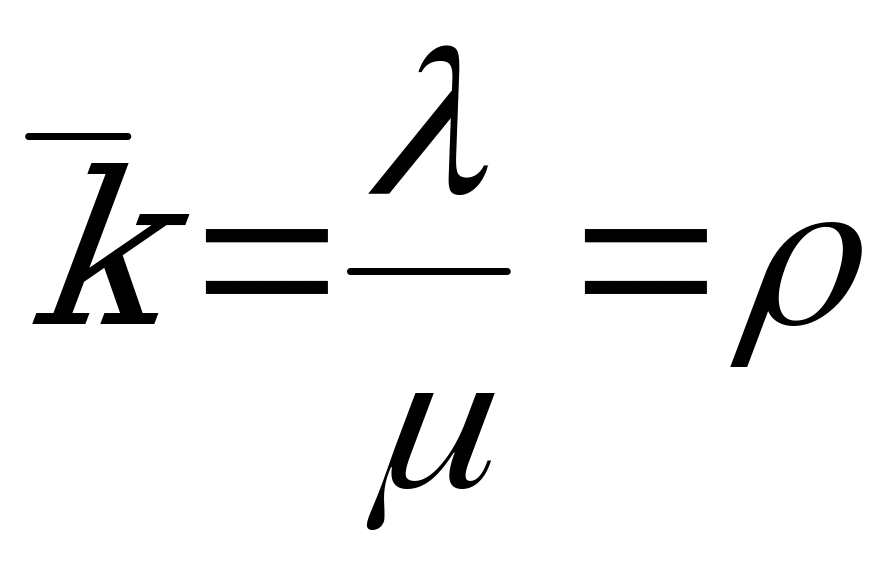 .
.
Среднее число заявок в очереди:  .
.
Среднее число заявок в СМО: 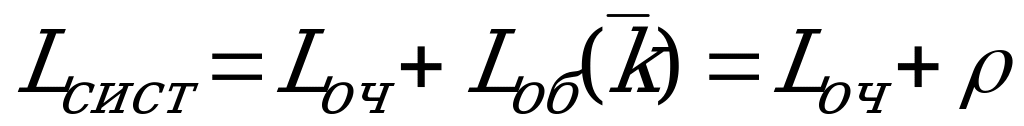 .
.
Среднее время пребывания заявки в СМО: 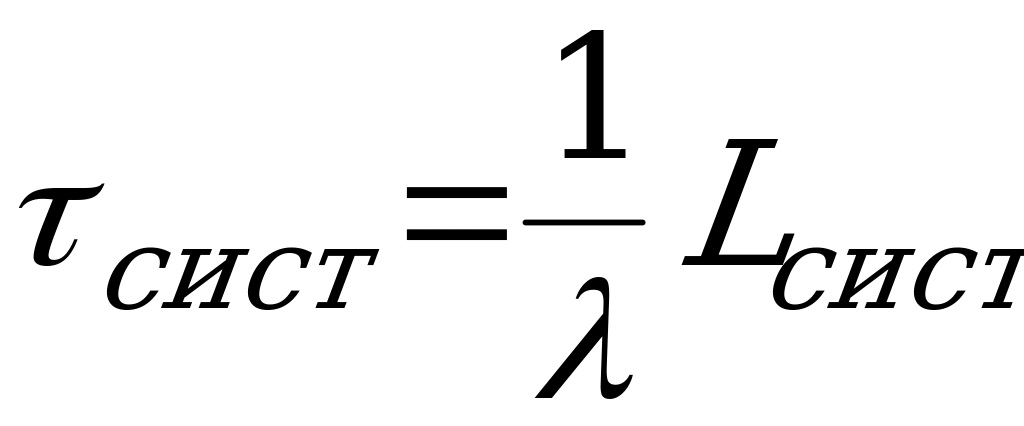 .
.
Вероятность того, что заявка окажется в очереди: 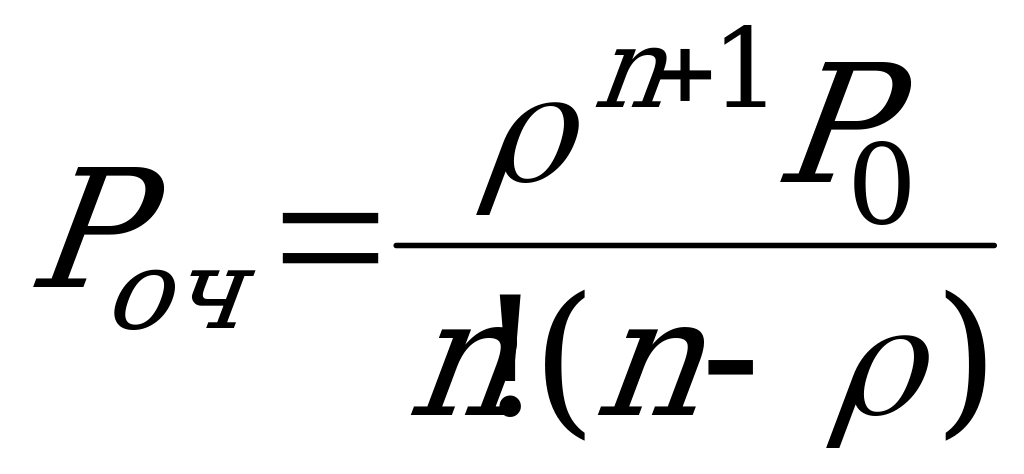 .
.
Среднее время пребывания заявки в очереди:  .
.
Многоканальная СМО с ограниченной очередью.
Число заявок в очереди не может превосходить некоторого заданного  .
.
Возможные состояния системы:
 - все ПО свободны;
- все ПО свободны;
 - один ПО занят, остальные свободны;
- один ПО занят, остальные свободны;
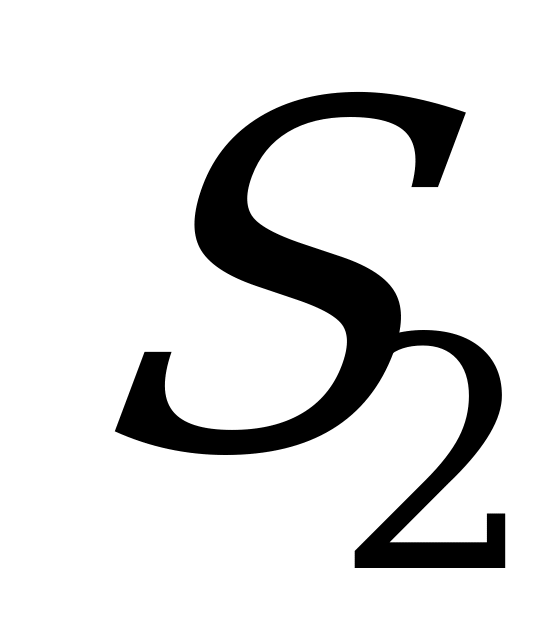 - заняты два ПО, остальные свободны;
- заняты два ПО, остальные свободны;
… … … … … … … … … … … … … … … … …
 - заняты все ПО, очереди нет
- заняты все ПО, очереди нет 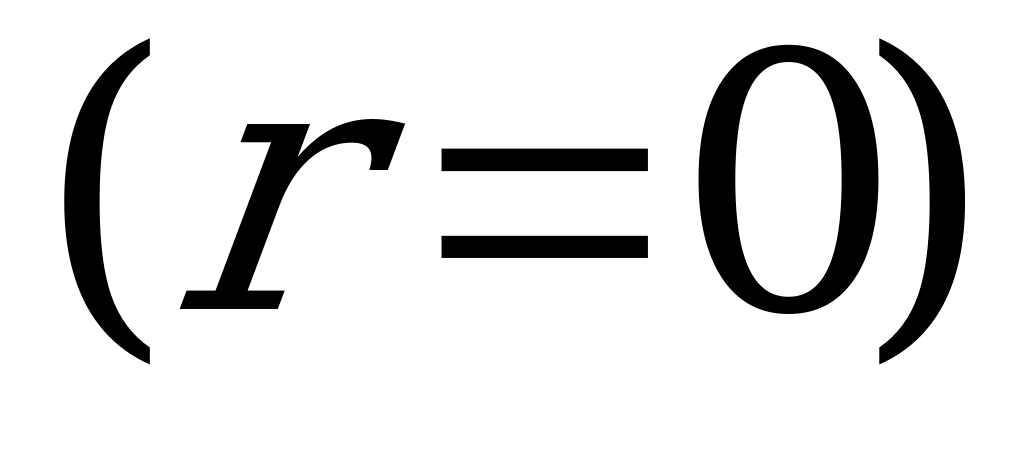 ;
;
 - заняты все ПО, одна заявка стоит в очереди
- заняты все ПО, одна заявка стоит в очереди  ;
;
… … … … … … … … … … … … … … … … …
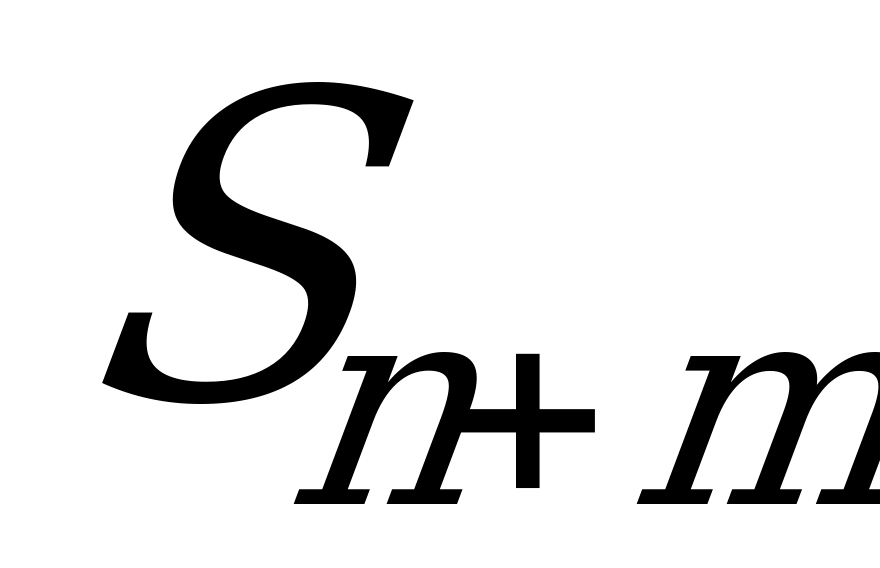 - заняты все ПО, в очереди
- заняты все ПО, в очереди  заявок (
заявок (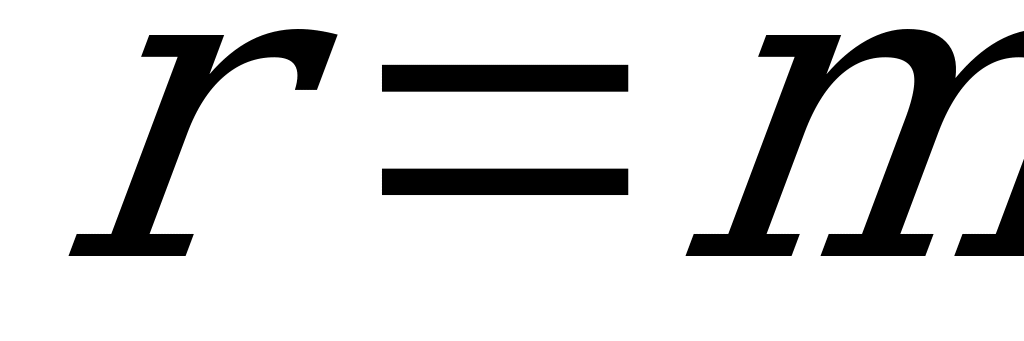 ).
).

Финальные вероятности (существуют при любом значении  ):
):
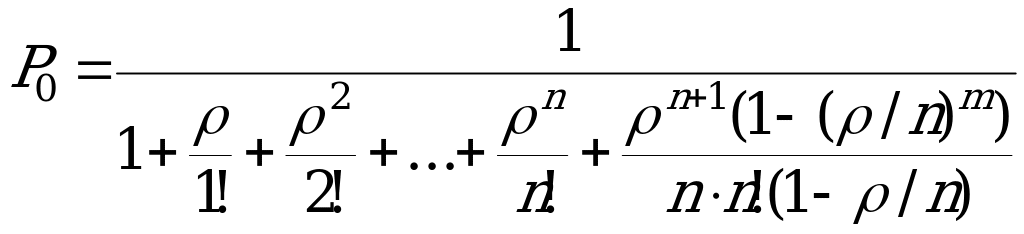 ;
;
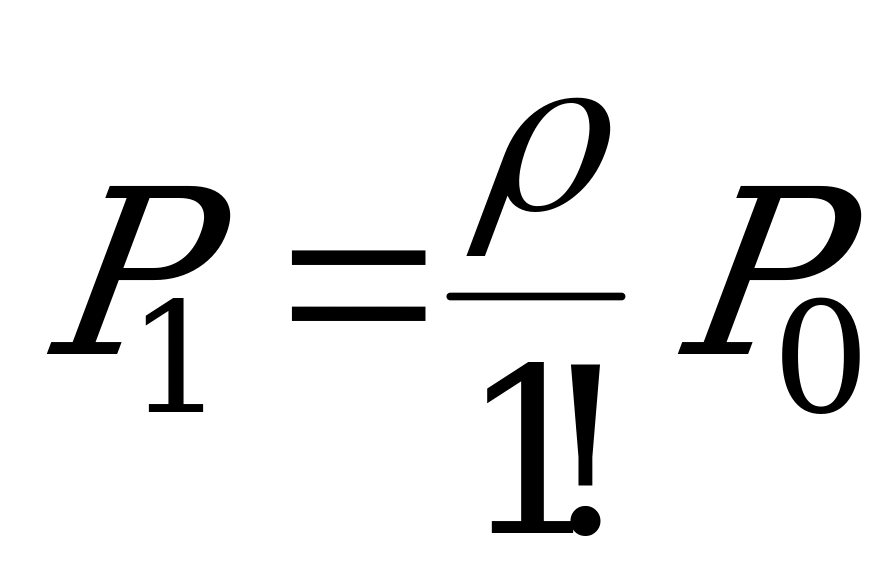 ,
,  , …,
, …,  , …,
, …, 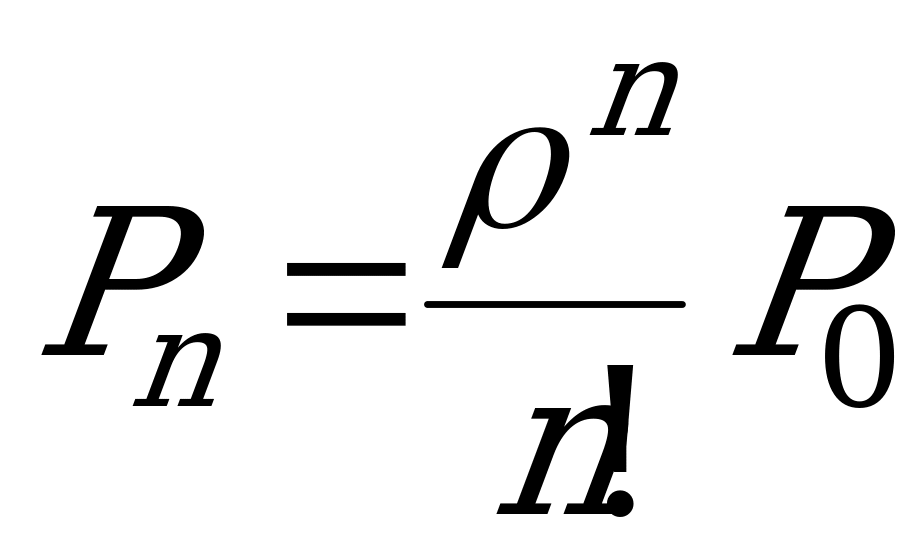 ,
,
 , …,
, …,  (
( ),
),
 - вероятность того, что
- вероятность того, что  приборов (каналов) заняты,
приборов (каналов) заняты,
 - вероятность того, что все ПО заняты, и в очереди находится
- вероятность того, что все ПО заняты, и в очереди находится  заявок.
заявок.
Вероятность отказа в обслуживании (равна вероятности того, что в очереди уже находится  заявок):
заявок): 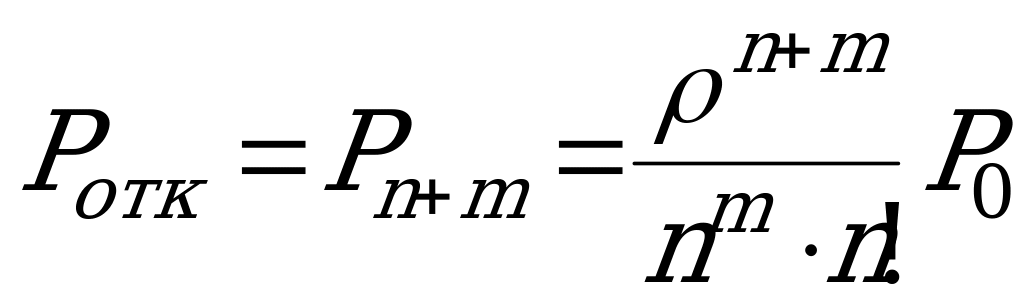 .
.
Относительная пропускная способность:  .
.
Абсолютная пропускная способность: 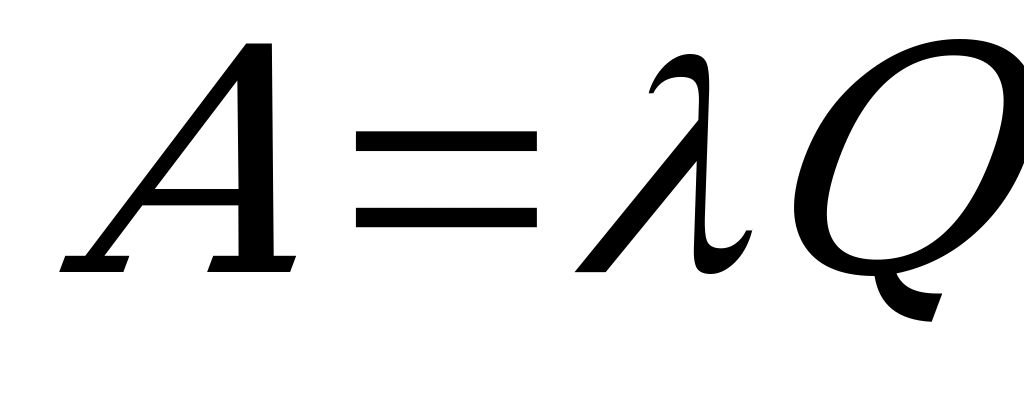 .
.
Среднее число занятых ПО: 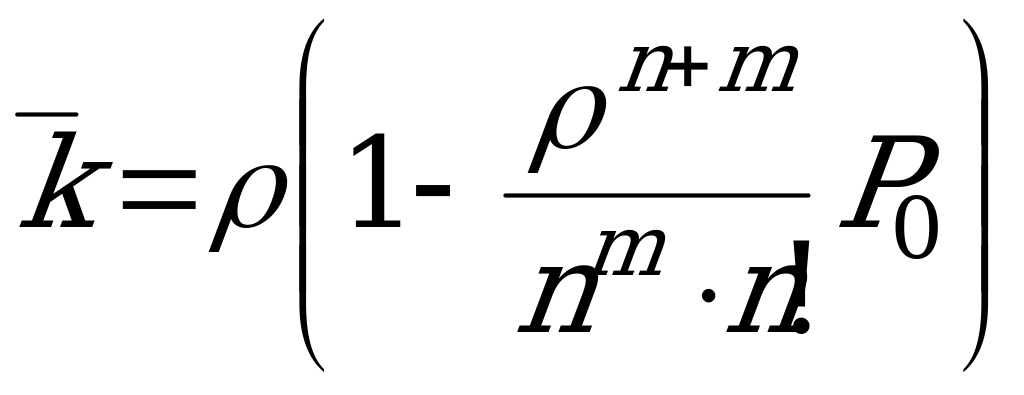 .
.
Среднее число заявок в очереди:
 .
.
Среднее число заявок в СМО:  .
.
Среднее время пребывания заявки в СМО: 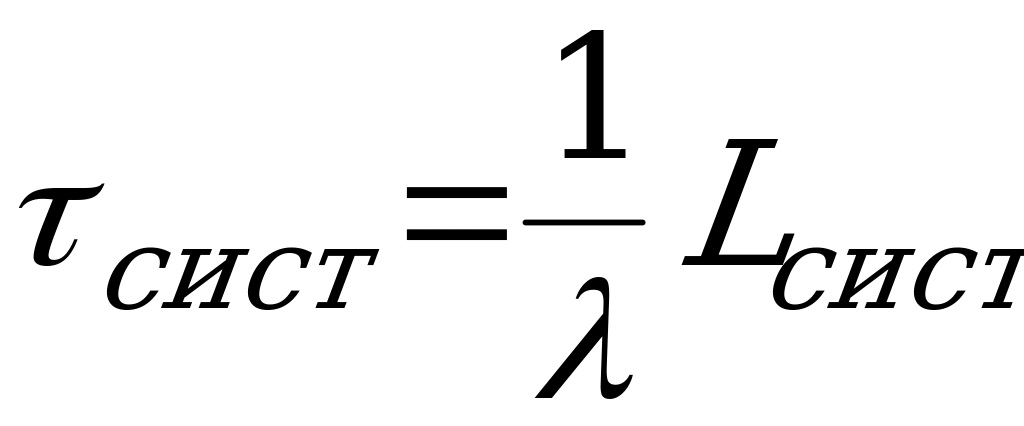 .
.
Среднее время пребывания заявки в очереди:  .
.
Пример 1. Одноканальная СМО представляет собой железнодорожную сортировочную станцию, на которую поступает простейший поток составов с интенсивностью  состава в час. Обслуживание (расформирование) состава длится случайное (показательное) время со средним значением
состава в час. Обслуживание (расформирование) состава длится случайное (показательное) время со средним значением  мин. В парке прибытия станции имеются два пути, на которых могут ожидать обслуживания прибывающие составы; если оба пути заняты, то составы вынуждены ждать на внешних путях.
мин. В парке прибытия станции имеются два пути, на которых могут ожидать обслуживания прибывающие составы; если оба пути заняты, то составы вынуждены ждать на внешних путях.
Определить характеристики работы железнодорожной станции.
Д ано:
ано:  состава в час;
состава в час;
 мин
мин  ч;
ч;
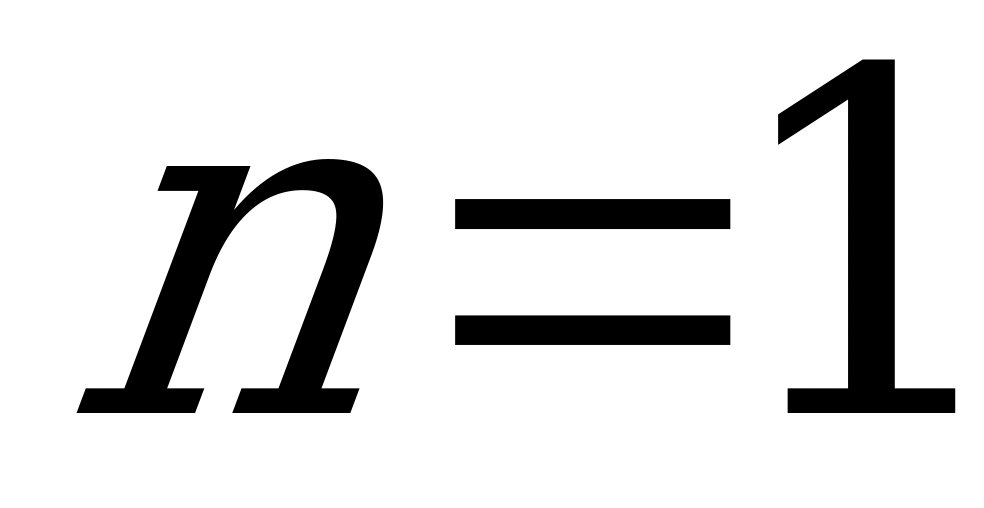 ,
, 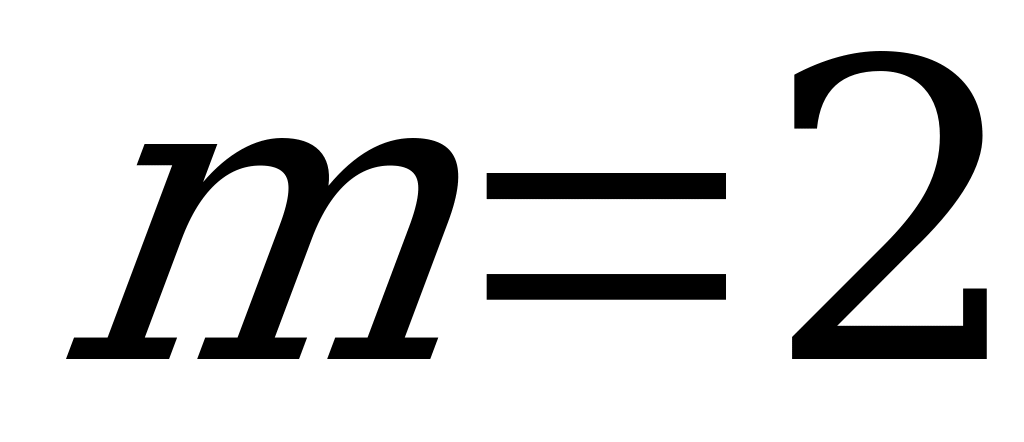 .
.
Решение.
Возможные состояния системы:
 - ПО свободен;
- ПО свободен;
 - ПО занят (обслуживает заявку), очереди нет (
- ПО занят (обслуживает заявку), очереди нет ( );
);
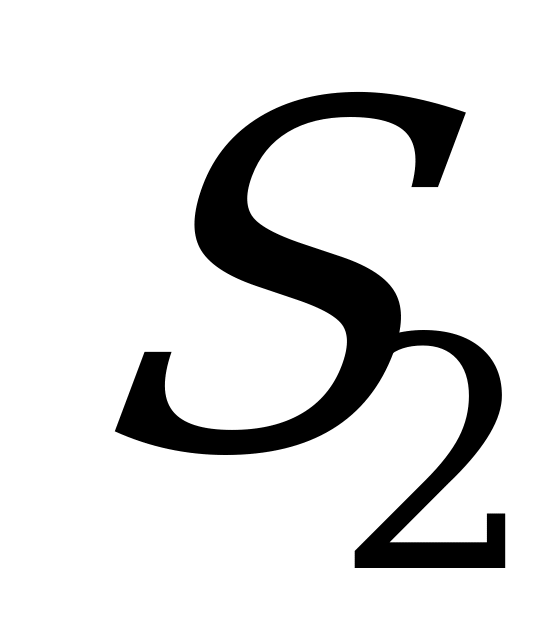 - ПО занят, одна заявка стоит в очереди (
- ПО занят, одна заявка стоит в очереди ( );
);
 - ПО занят, две заявки стоят в очереди (
- ПО занят, две заявки стоят в очереди ( ).
).


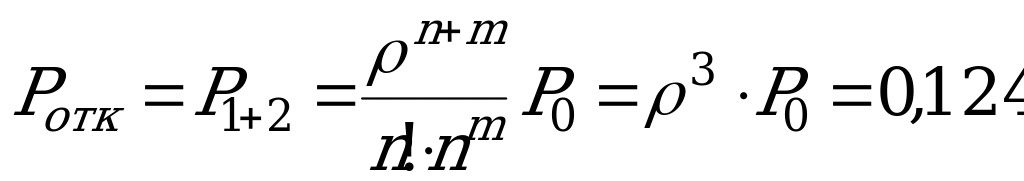

 , где
, где 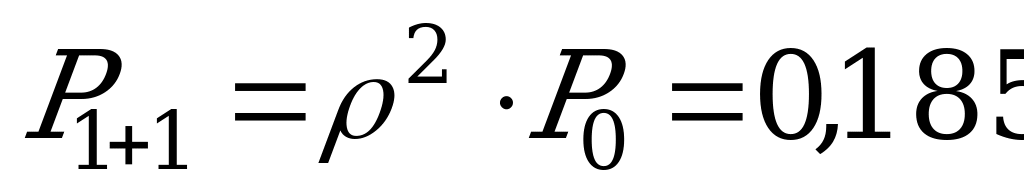 ,
,
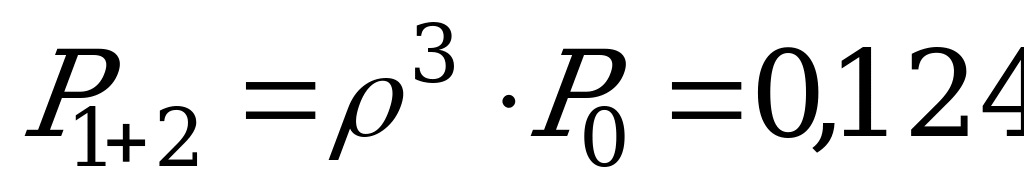 , тогда
, тогда
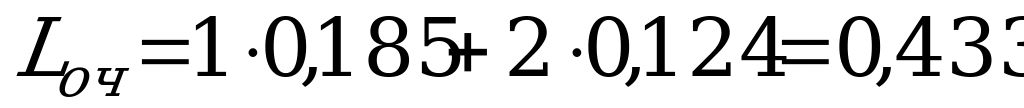 (состава)
(состава)
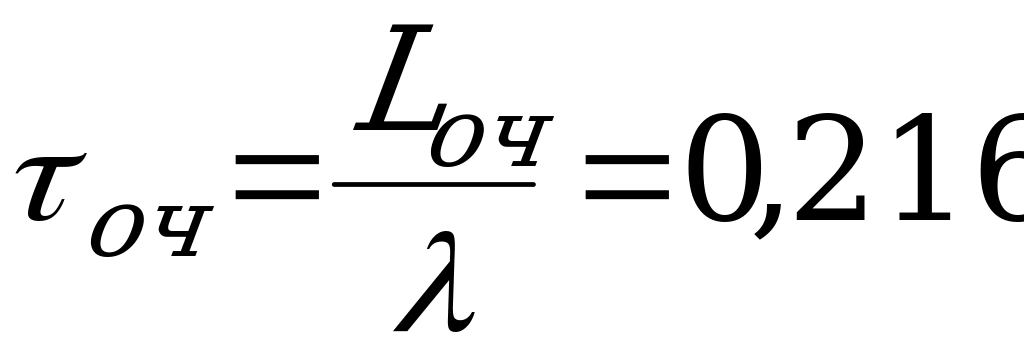 ч
ч  мин
мин
 мин
мин
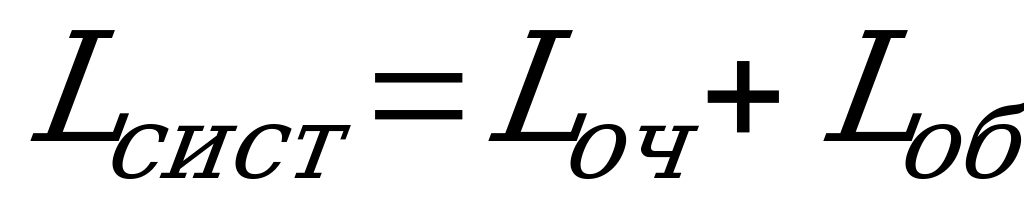 , где
, где 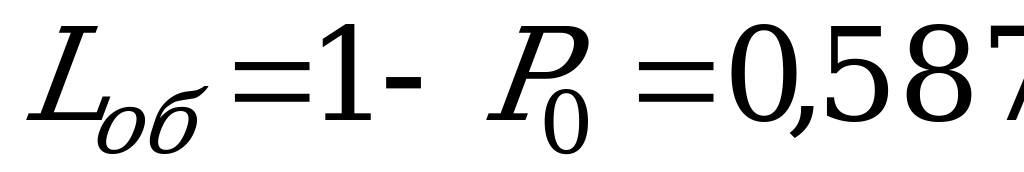 , тогда
, тогда
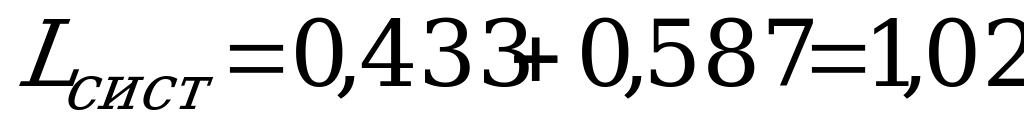 (состава).
(состава).
Пример 2. В офис некоторой фирмы поступают звонки на многоканальный телефон с интенсивностью  звонков в час, а средняя продолжительность разговора
звонков в час, а средняя продолжительность разговора 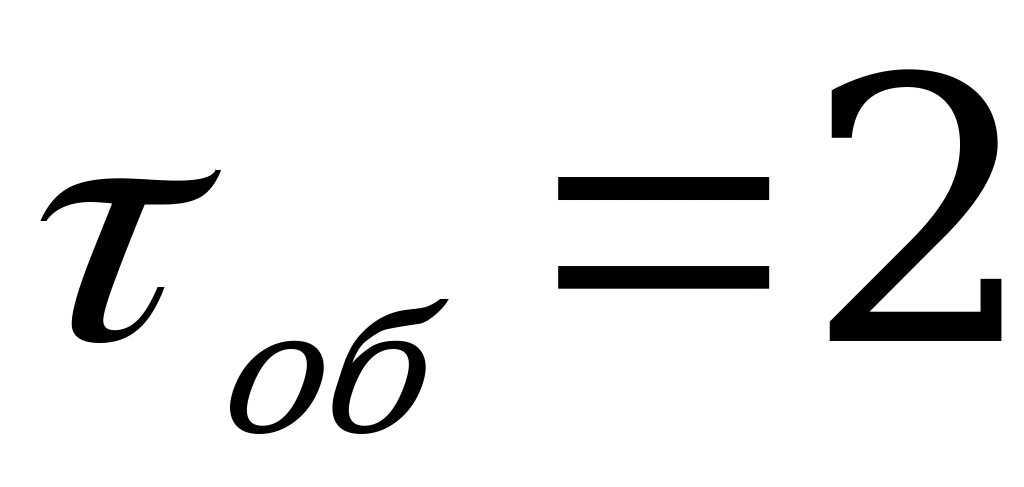 минуты. Определить оптимальное число телефонных каналов, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 90 заявок на переговоры.
минуты. Определить оптимальное число телефонных каналов, если условием оптимальности считать удовлетворение в среднем из каждых 100 заявок не менее 90 заявок на переговоры.

Дано: 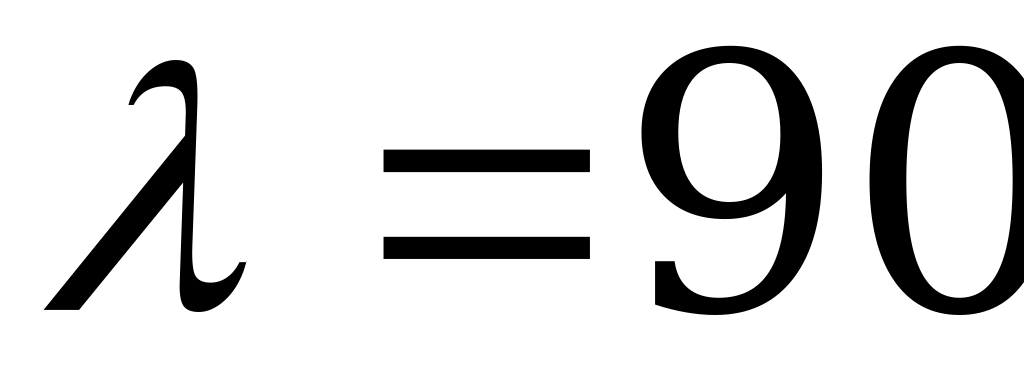 заявок в час; Найти:
заявок в час; Найти:  .
.
 мин
мин 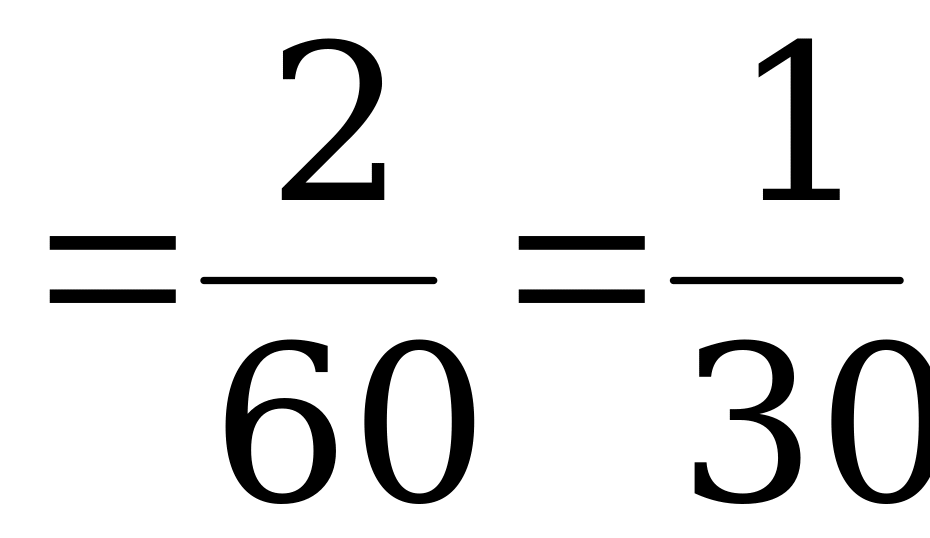 ч;
ч;
 ;
;  .
.
Решение.
Интенсивность нагрузки канала 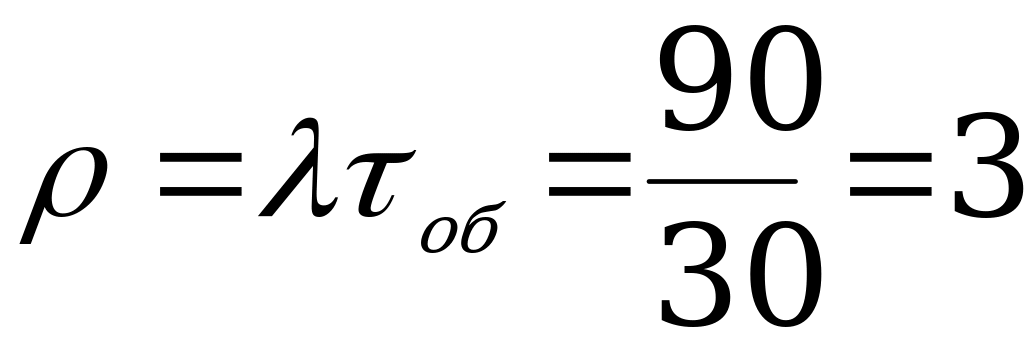 , т.е. за время среднего по продолжительности телефонного разговора
, т.е. за время среднего по продолжительности телефонного разговора  мин поступает в среднем 3 заявки на переговоры.
мин поступает в среднем 3 заявки на переговоры.
Будем постепенно увеличивать число каналов 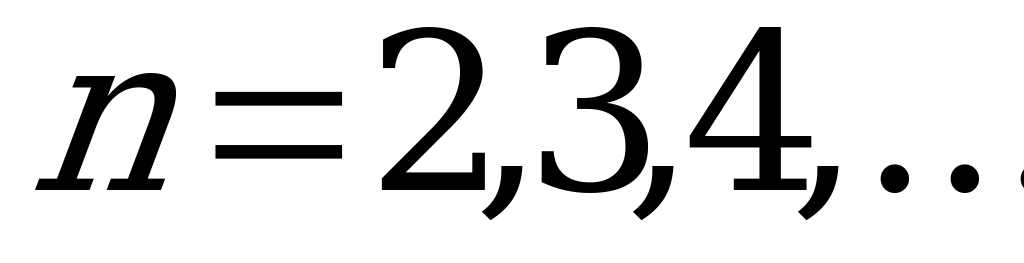 и определим для получаемой
и определим для получаемой  -канальной СМО характеристики обслуживания. Значения характеристик СМО приведены в таблице.
-канальной СМО характеристики обслуживания. Значения характеристик СМО приведены в таблице.
| Характеристика обслуживания | Число телефонных каналов |
| 1 | 2 | 3 | 4 | 5 | 6 |
| Относительная пропускная способность  | 0,25 | 0,47 | 0,65 | 0,79 | 0,90 | 0,95 |
| Абсолютная пропускная способность  | 22,5 | 42,3 | 58,5 | 71,1 | 81 | 85,5 |
По условию  , следовательно, в офисе необходимо установить 5 телефонных каналов (в этом случае
, следовательно, в офисе необходимо установить 5 телефонных каналов (в этом случае  ). При этом в час будет обслуживаться, в среднем, 81 заявка (
). При этом в час будет обслуживаться, в среднем, 81 заявка (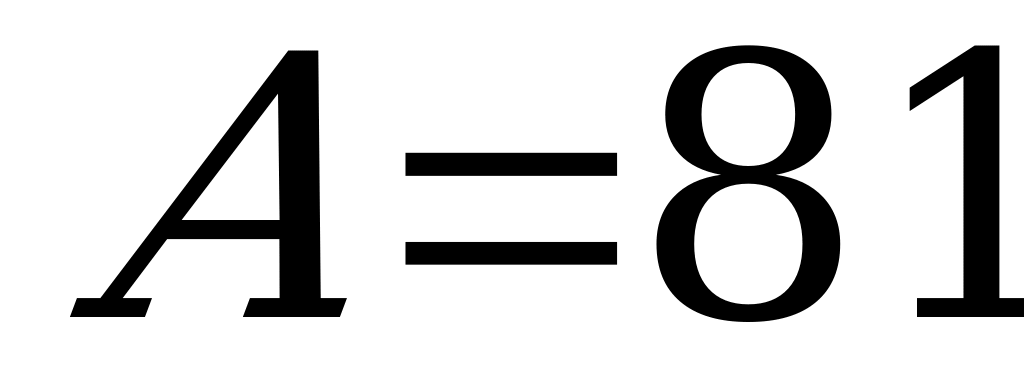 ), а среднее число занятых телефонных каналов
), а среднее число занятых телефонных каналов 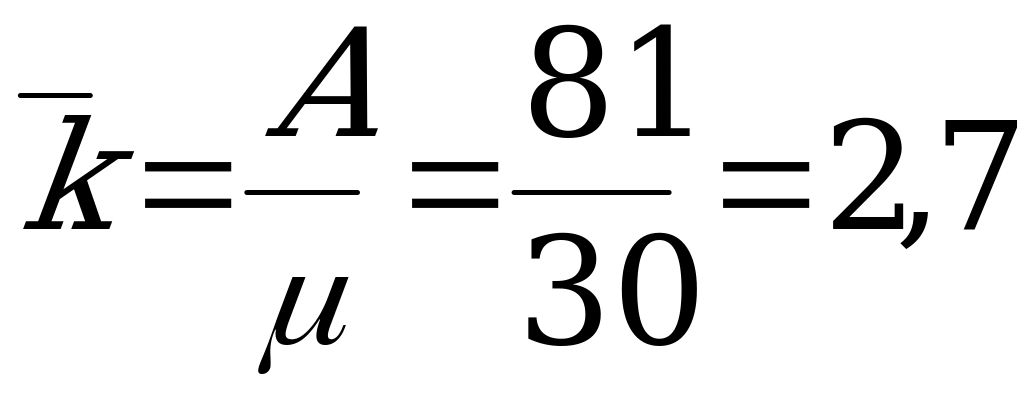 .
.
Практическая работа по теме: «Системы массового обслуживания».
З
Вар. 24
адание. Для СМО с заданными параметрами:
а) перечислить возможные состояния,
б) построить граф состояний,
в) составить уравнения для финальных вероятностей,
г) определить характеристики работы  .
.
Дано: интенсивность входного потока заявок  заявок/ед.врем,
заявок/ед.врем,
среднее число заявок, обслуживаемых в единицу времени одним ПО  заявок/ед.врем,
заявок/ед.врем,
количество приборов обслуживания  , число мест в очереди
, число мест в очереди  не ограничено.
не ограничено.
Решение. Система с заданными  и
и  является многоканальной с неограниченной очередью.
является многоканальной с неограниченной очередью.
Возможные состояния системы:
 - в СМО нет заявок (все ПО свободны, очереди нет);
- в СМО нет заявок (все ПО свободны, очереди нет);
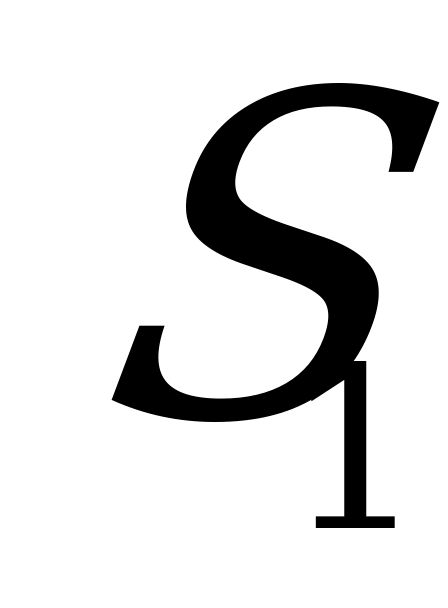 - в СМО находится одна заявка (один ПО занят, очереди нет);
- в СМО находится одна заявка (один ПО занят, очереди нет);
 - в СМО находятся две заявки (два ПО заняты, очереди нет);
- в СМО находятся две заявки (два ПО заняты, очереди нет);
 - в СМО находятся три заявки (заняты все три ПО, очереди нет);
- в СМО находятся три заявки (заняты все три ПО, очереди нет);
 - в СМО находятся четыре заявки (заняты все три ПО, одна заявка стоит в очереди);
- в СМО находятся четыре заявки (заняты все три ПО, одна заявка стоит в очереди);
… … … … … … … … … … … … … … … … …
… … … … … … … … … … … … … … … …
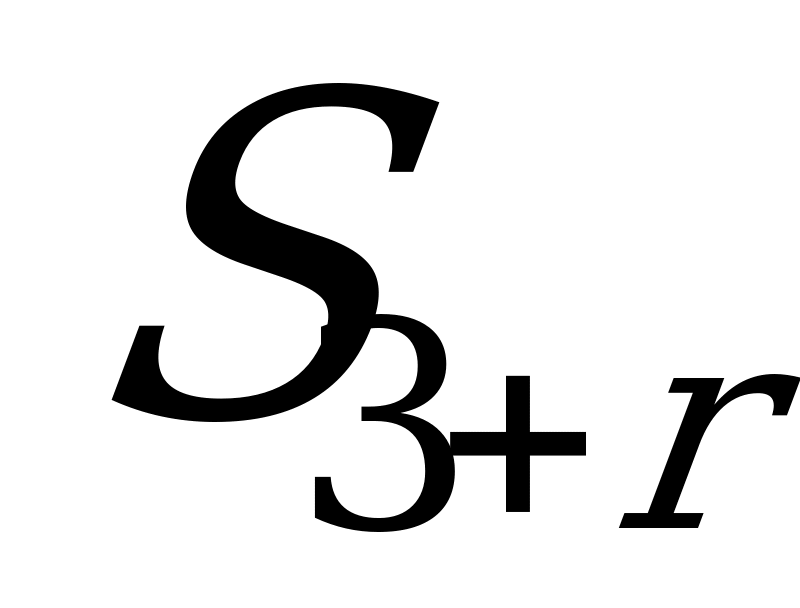 - заняты все ПО,
- заняты все ПО,  заявок стоит в очереди;
заявок стоит в очереди;
… … … … … … … … … … … … … … … … …
Уравнения
для финальных вероятностей:




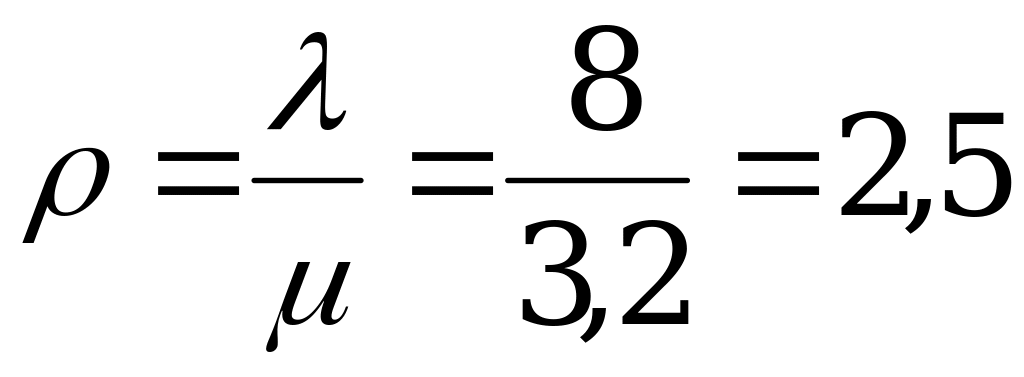 (среднее время обслуживания одной заявки
(среднее время обслуживания одной заявки  ед.врем.
ед.врем.  0,31)
0,31)
 .
.
Относительная пропускная способность:  . Абсолютная пропускная способность:
. Абсолютная пропускная способность:  .
.
Среднее число занятых ПО:  .
.
Среднее число заявок в очереди:

.
Среднее число заявок в СМО: 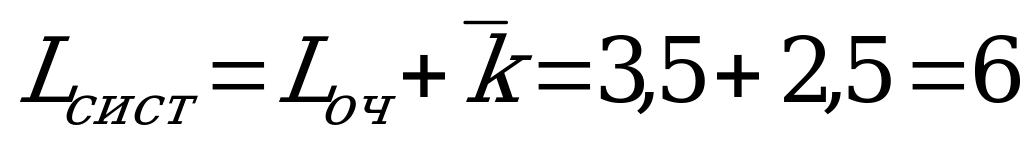 (заявок).
(заявок).
Среднее время пребывания заявки в очереди:  (ед.времени).
(ед.времени).
Среднее время пребывания заявки в СМО:  (ед.времени).
(ед.времени).
Практическая работа по теме: «Системы массового обслуживания».
З
Вар. 25
адание. Для СМО с заданными параметрами:
а) перечислить возможные состояния,
б) построить граф состояний,
в) составить уравнения для финальных вероятностей,
г) определить характеристики работы  .
.
Дано: интенсивность входного потока заявок  заявок/ед.врем,
заявок/ед.врем,
среднее число заявок, обслуживаемых в единицу времени одним ПО  заявок/ед.врем,
заявок/ед.врем,
количество приборов обслуживания  , число мест в очереди
, число мест в очереди  .
.
Решение. Система с заданными  и
и  является многоканальной без очереди.
является многоканальной без очереди.
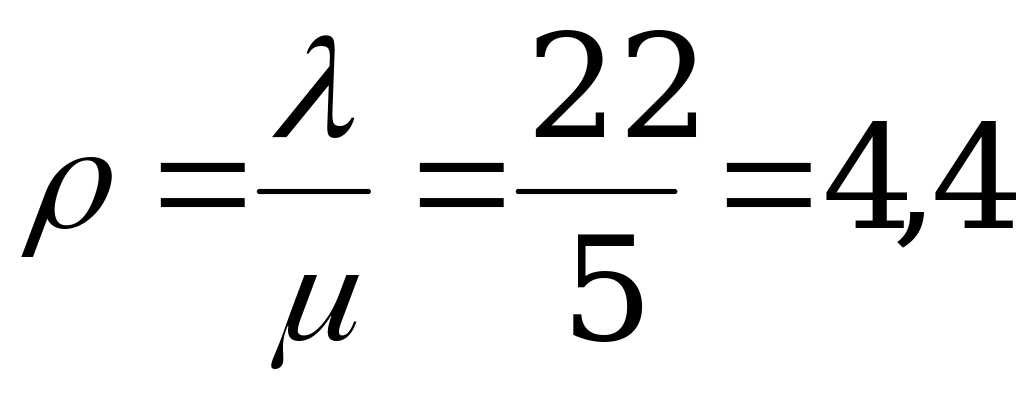
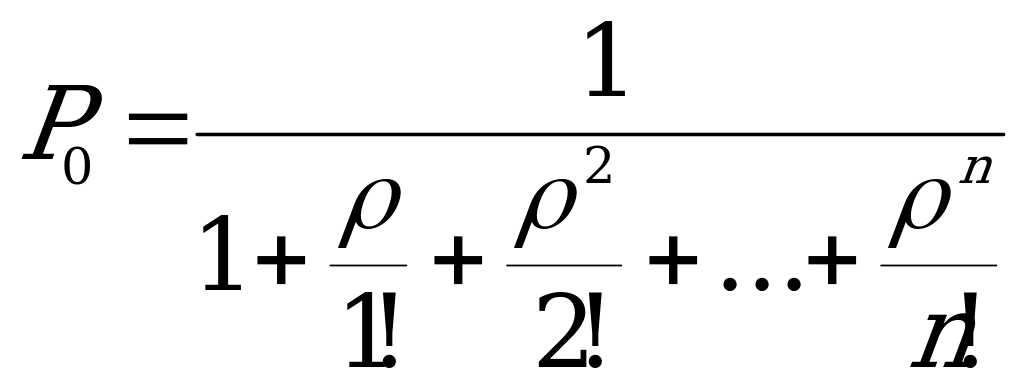 ;
;  ;
;
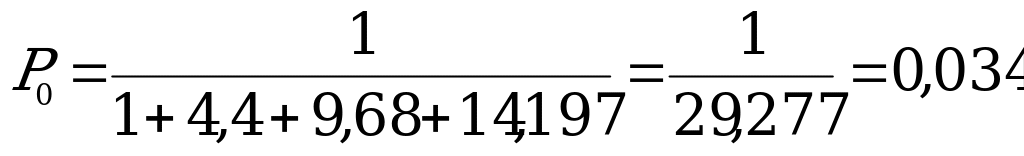 .
.

Относительная пропускная способность:  .
.
Абсолютная пропускная способность:  .
.
Среднее число занятых ПО:  .
.
Среднее время пребывания заявки в СМО: 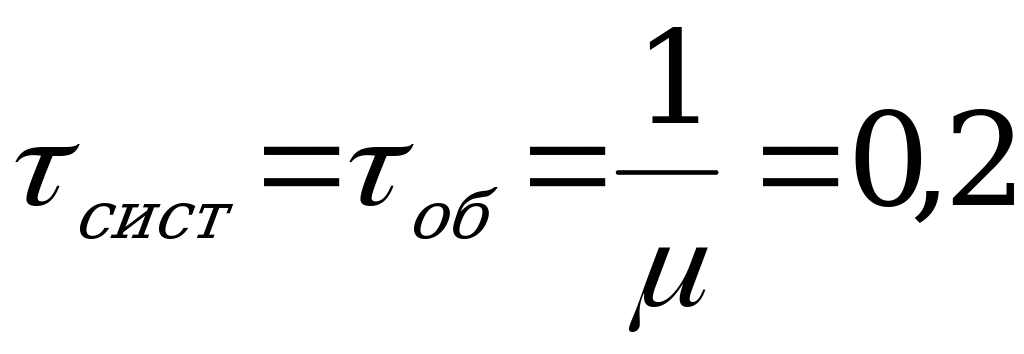 (ед.времени).
(ед.времени).














 ример. Построить граф состояний следующего случайного процесса. Техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное, случайное время.
ример. Построить граф состояний следующего случайного процесса. Техническое устройство состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего мгновенно начинается ремонт узла, продолжающийся заранее неизвестное, случайное время. 









 опадания случайной величины в этот интервал. Геометрически эта вероятность равняется площади соответствующей криволинейной трапеции.
опадания случайной величины в этот интервал. Геометрически эта вероятность равняется площади соответствующей криволинейной трапеции. 











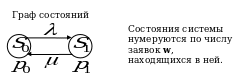

 озможные состояния системы:
озможные состояния системы:
 ;
; 

 - все
- все 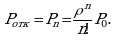

 Возможные состояния системы:
Возможные состояния системы:



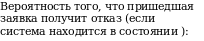
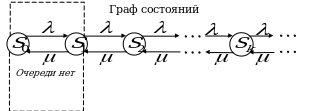
 - заняты все ПО,
- заняты все ПО, 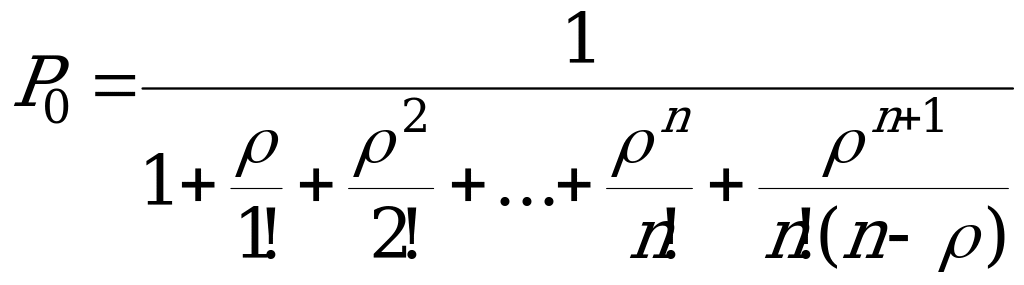 ;
;
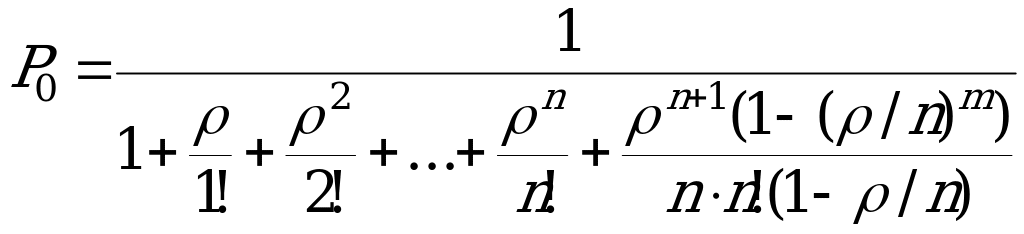 ;
; .
. ано:
ано: 

 … … … … … … … … … … … … … … … …
… … … … … … … … … … … … … … … … 

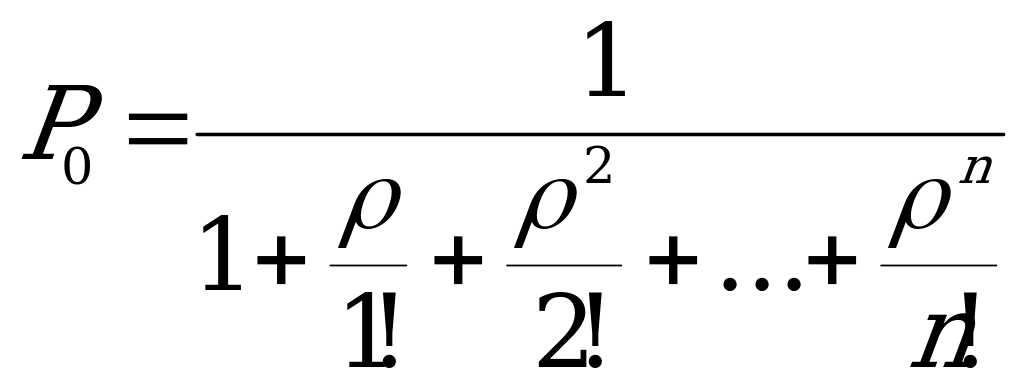 ;
;  ;
;









