Системы счисления. Общие сведения
Цели урока:
образовательная – ввести понятия систем счисления, ознакомить с классами систем счисления, машинными системами счисления, алгоритмом перевода из десятичной системы счисления в машинные с примерами, алгоритмом перевода из машинных систем счисления в десятичную систему счисления, а также с алгоритмом перевода из двоичной системы счислении в восьмеричную и шестнадцатеричную;
воспитательная – формирование логического мышления: восприятие компьютера, как инструмента, работающего по законам логики;
развивающие – становление и развитие логического мышления: развитие познавательного интереса; формирование информационной культуры и потребности приобретения знаний.
Просмотр содержимого документа
«Системы счисления. Общие сведения. 10 класс»

ИНФОРМАТИКА.
Системы счисления.

Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.

Системы счисления подразделяются на
- Позиционные
- Непозиционные

Н ЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ.
- Непозиционной называется такая система, у которой количественное значение цифры зависит от ее начертания и не зависит от положения, т.е. каждый знак всегда изображает одно и то же число.

П ОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ.
- Большинство систем счисления относятся к позиционным. В них значение каждой цифры изменяется в зависимости от места (позиции), на котором она находится.
К позиционным относятся:
- Двоичная система счисления
- Восьмеричная и шестнадцатеричная системы счислений
- Десятичная система счисления и др.
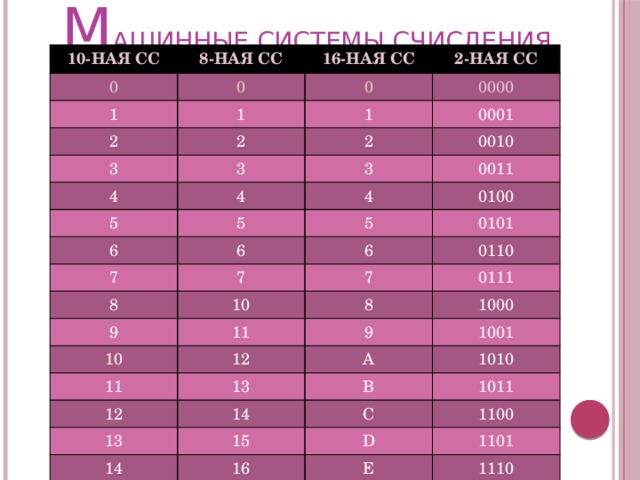
М АШИННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
10-НАЯ СС
8-НАЯ СС
0
16-НАЯ СС
0
1
2-НАЯ СС
2
0
1
2
3
1
0000
0001
4
2
3
5
4
0010
3
0011
4
5
6
0100
7
5
6
8
7
0101
6
0110
7
10
9
0111
8
11
10
9
1000
12
11
1001
12
A
13
13
14
B
1010
1011
C
15
14
1100
D
16
15
1101
E
17
1110
F
1111

Д ЕСЯТИЧНАЯ СИСТЕМА ИСЧИСЛЕНИЯ
- По плотности записи информации уступает многим другим системам счисления, но по удобству пользования человеком превосходит другие системы счисления.

П ЕРЕВОД ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ С ЧИСЛЕНИЯ В МАШИННЫЕ.
П РАВИЛА:
- Последовательно выполнять деление исходного числа и получаемых целых частных на основании новой системы счисления (двоичной, восьмеричной или шестнадцатеричной) , до тех пор пока не получится частное равное нулю.
- Записать полученное число в новой системе счисления, для чего записать полученные остатки в обратном порядке.

Например :
- перевести число 153 10 в 2-ную, 8-ную и 16-ную СС:
153 : 2 = 76 (ост 1)
76:2=38 (ост 0)
38:2=19 (ост 0)
19:2=9(ост 1)
9:2=4(ост 1)
4:2=1(ост 0)
2:2=1(ост 0)
1:2=0(ост 1)
153:8=19(ост 1)
19:8=2(ост 3)
2:8=0(ост 2)
153:16=9(ост9)
9:16=0(ост 9)
153 10 = 1001100 12 = 231 8 = 99 16

П ЕРЕВОД ЧИСЕЛ ИЗ МАШИННЫХ СИСТЕМ В ДЕСЯТИЧНУЮ СПОСОБОМ СТЕПЕННОГО РЯДА
П РАВИЛА:
- Сформулировать координатную степенную ось
- Разложить число в виде степенного ряда
- Подсчитать сумму произведении степенного ряда

Например :
Перевести числа 101 2 , 123 8 , 123 16 в 10-ную СС:
1 2 0 1 1 2 0 =1*2 0 + 0*2 1 =1*2 2 =5 10
1 2 2 1 3 8 0 =3*8 0 +2*8 1 +1*8 2 =81 10
1 2 2 1 3 16 0 =3*16 0 =2*16 1 +1*16 2 =289 10

Д ВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
- Двоичная система счисления —
это позиционная система счисления с целочисленным основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).

П еревод из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно.
Алгоритм перевода из двоичной системы счисления в восьмеричную таков:
- разбить на группы по 3 цифры справа налево начиная с младшего разряда;
- если до полной группы цифр не хватает, то добавляем нужное количество нулей справа;
- затем каждую тройку цифр заменяем соответственно цифрой восьмеричной системы счисления;
- дробную часть разбиваем от запятой вправо на группы по 3 цифры (в случае нехватки цифр нули приписываем слева);
Обратный переход: осуществляется заменой каждой восьмеричной цифры ее двоичным эквивалентом.
- Для шестнадцатеричной системы счисления цифры в двоичной системе счисления группируют по 4.
- Для удобства переводов можно использовать таблицы переводов:
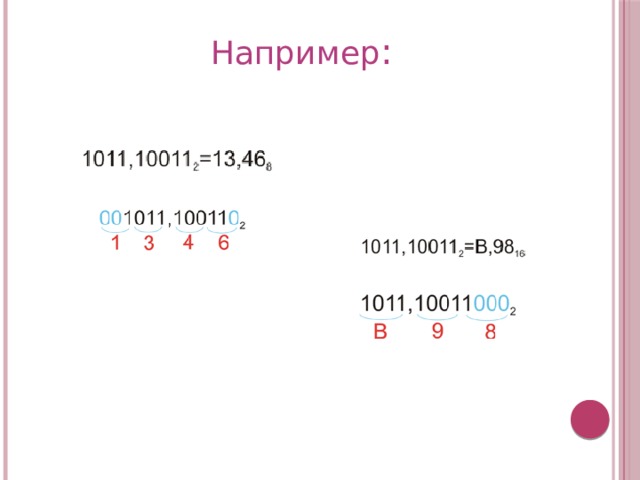
Например :

В ОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
- в осьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры 0 до 7.
- Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триады двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

ш ЕСТНАДЦАТЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ.
- Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

































