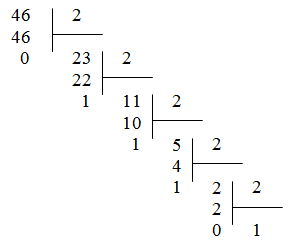Системы счисления. Представление числовой информации в различных системах счисления

Тема: "Системы счисления. Представление числовой информации в различных системах счисления. Перевод чисел из десятичной системы счисления в двоичную и наоборот".

Цель работы: 

Получение практических навыков преобразования чисел из десятичной системы счисления в двоичную и наоборот

Количество часов на выполнение работы

Продолжительность выполнения данной практической работы составляет 2 академических часа.

Оборудование

• тетрадь;

• ручка (карандаш);

• калькулятор.

Краткие теоретические сведения

Система счисления – совокупность приемов и правил для обозначения и наименования чисел. Системы счисления подразделяются на позиционные (десятичная, двоичная, восьмеричная, шестнадцатеричная) и непозиционные (римская система счисления).

Алфавит системы счисления – множество всех символов (знаков), используемых для записи чисел в данной системе счисления.

Система счисления называется непозиционной, если количественный эквивалент значения любого символа не зависит от его положения (позиции) в коде числа.

Пример: Римская система счисления (2,5тыс. лет до н.э.) 1 -I, 10 - Х, 100 -C, 1000 -M, 5 -V, 50 -L, 500 -D

Для записи числа его раскладывают на сумму цифр 1000, 500, 100, 50, 10, 5, 1.

Система счисления называется позиционной, если количественный эквивалент (значение символа) зависит от его положения в записи числа.

Базисом позиционной системы счисления называется последовательность чисел, каждое из которых определяет количественный эквивалент (вес) символа в зависимости от его места в коде числа.

Основанием позиционной системы счисления называется целое число, которое возводится в степень для получения базиса. Основание в позиционной системе счисления показывает, во сколько раз изменяется вес цифры при перемещении ее на соседнюю позицию. За основание системы счисления можно принять любое натуральное число n (n=1 - недопустимо, т.к. получим унарную систему счисления).

Для записи чисел в системе счисления с основанием q требуется q различных знаков (цифр), изображающих числа 0,1,2,…,q-1.

Основание позиционной системе счисления равно количеству знаков в ее алфавите.

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Разложение двоичного числа:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³+ 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001: 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так: 10001001₂ = 137₁₀

Перевод числа из десятичной системы в двоичную:

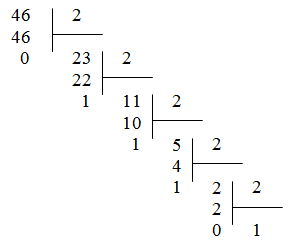
Рисунок 1 – Перевод числа из десятичной системы счисления в двоичную

Задания по практической работе

1. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101011₂, 10001011110₂, 461₈, 2644₈, 510₁₀, 1975₁₀, 3DF₁₆, 1A0A₁₆.

2. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1001110₂, 11000111011₂, 317₈, 3710₈, 252₁₀, 3999₁₀, 80C₁₆, 2FF2₁₆.

3. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101100₂, 11001100110₂, 363₈, 4114₈, 515₁₀, 2345₁₀, 5АЕ₁₆, 3ВВС₁₆.

4. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1000111₂, 11100011011₂, 415₈, 3111₈, 260₁₀, 2901₁₀, A07₁₆, 9AA4₁₆.

5. Перевести числа в двоичную, восьмеричную, десятичную и шестнадцатеричную системы счисления: 1101010₂, 10000011110₂, 333₈, 2077₈, 131₁₀, 3222₁₀, 77F₁₆, 5D74₁₆.

Контрольные вопросы

1. Что такое система счисления?

2. Какие системы счисления называются непозиционными?

3. Что такое основание, алфавит и базис системы счисления?

4. По какому правилу осуществляется перевод чисел из десятичной системы в двоичную и наоборот?