Система двух линейных уравнений с двумя переменными

Автор : учитель математики

Олейник Татьяна Алекандровна

1.Что называют системой двух линейных уравнений с двумя переменными?

2.Знак системы?

3.Что называют решением системы двух уравнений с двумя переменными?

4.Что значит решить систему уравнений?

Способы решения систем двух линейных уравнений с двумя переменными

1.Способ подстановки

2.Способ алгебраического сложения

3.Графический способ

4.Формулы Крамера

5.Метод подбора

Способ подстановки

1. Из одного уравнения системы (всё равно из какого)выразить одну переменную через другую, например, y через x .

2. Полученное выражение подставить в другое уравнение системы и получить уравнение с одной переменной x .

3. Решить это уравнение, найти значение x .

4. Подставить найденное значение x в выражение для y и найти значение y .

5. Записать ответ в виде упорядоченной пары ( x;y)

Решить систему уравнений методом подстановки

-3x=-3

X=-3: (-3)

X=1

y=4-2 * 1

y =2

Ответ: (1;2)

2x+y=4

y=4-2x

X+2*(4-2x)=5

X+8-4x=5

X-4x=5-8

Способ алгебраического сложения

1.Уравнять модули коэффициентов при одной из переменных;

2.Складывая или вычитая полученные уравнения, найти значение одной переменной;

3.Подставить найденное значение в одно из уравнений исходной системы и найти значение второй переменной;

4. Записать ответ в виде упорядоченной пары ( x;y).

Решить систему уравнений способом алгебраического сложения

X+2y=5

X+2 *2=5

X+4=5

X=1

Ответ: (1;2)

3 y =6

y=2

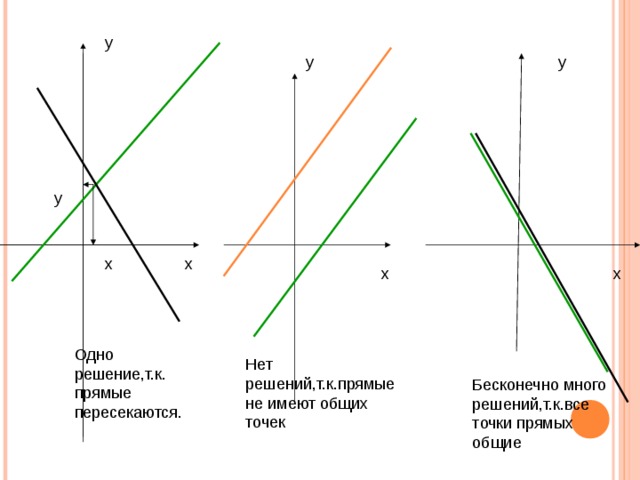
Графический способ

1 .Выразить y через x из каждого уравнения системы

2.Построить графики функций

в одной координатной плоскости.

3.Найти координаты общей точки графиков ( если графики имеют общую точку)

4 Записать ответ в виде x≈… И y≈

y

y

y

y

x

x

x

x

Одно решение,т.к. прямые пересекаются.

Нет решений,т.к.прямые не имеют общих точек

Бесконечно много решений,т.к.все точки прямых общие

Достоинство графического способа – н аглядность.

Недостаток графического способа–

приближённые значения переменных

Если система уравнений не имеет решений , то она называется н есовместной.

Если система уравнений имеет бесконечно много решений, то она называется неопределённой

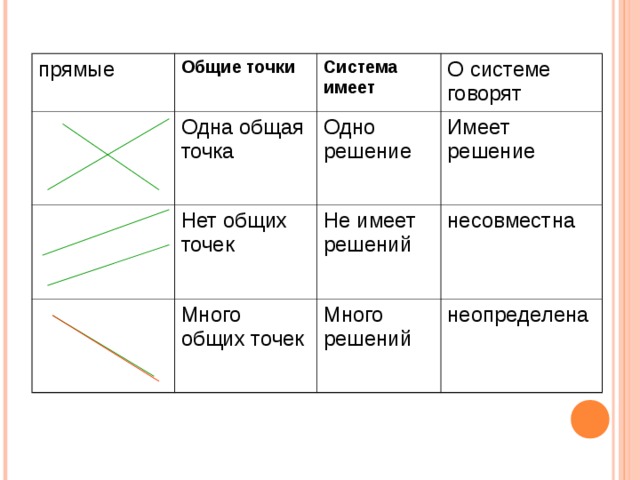
прямые

Общие точки

Одна общая точка

Система имеет

Нет общих точек

Одно решение

О системе говорят

Не имеет решений

Много общих точек

Имеет решение

Много решений

несовместна

неопределена

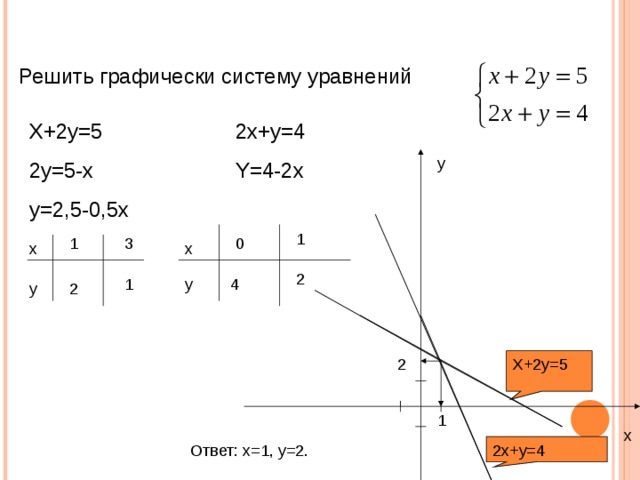
Решить графически систему уравнений

X+2y=5

2y=5-x

y=2,5-0,5x

2x+y=4

Y=4-2x

y

1

1

0

3

x

x

2

4

y

1

2

y

2

X+2y=5

1

x

2x+y=4

Ответ: x=1, y=2.

Формулы Крамера

∆ ---- главный определитель

вспомогательные определители

a1 b1

a2 b2

∆ =

=a1 * b2 –a2 * b1

1 .Если главный определитель не равен нулю, то система имеет одно решение.

2.Если главный определитель равен нулю, то:

Нет решений, если вспомогательные определители не равны нулю;

Много решений, если вспомогательные определители равны нулю

C1 b1

C2 b2

=

=c1 * b2 –c2 * b 1

x

x

A1 c1

A2 c2

=

=a1 * c2 –a2* с1

Решить систему по формулам Крамера

• 2

2 1

= 1*1-2*2=-3 ≠0

=-3 ; (-3) =1

5 2

4 1

= 5*1-4*2=-3

-6 : (-3) =2

1 5

2 4

=1*4-2*5=-6

Ответ: (1;2)

Метод подбора

1. Назови решение системы уравнений:

2.К уравнению x+y=6 добавь такое уравнение, чтобы решением системы была упорядоченная пара чисел (4;2)

3. Придумать систему уравнений такую, чтобы её решением была упорядоченная пара чисел (5;2)

О количестве решений системы уравнений по виду системы

Одно решение

Одно решение

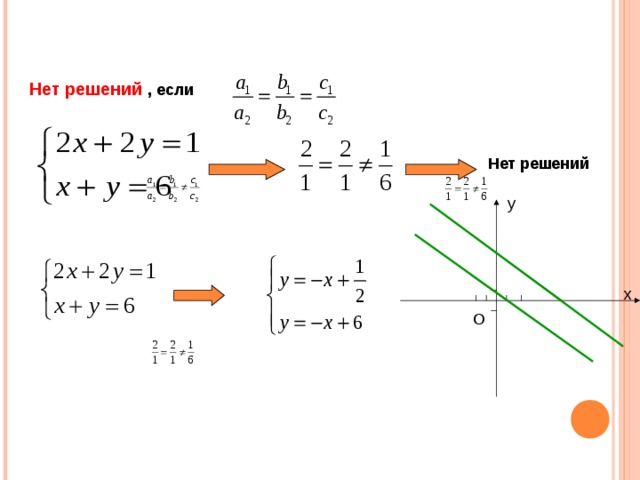
Нет решений , если

Нет решений

y

x

О

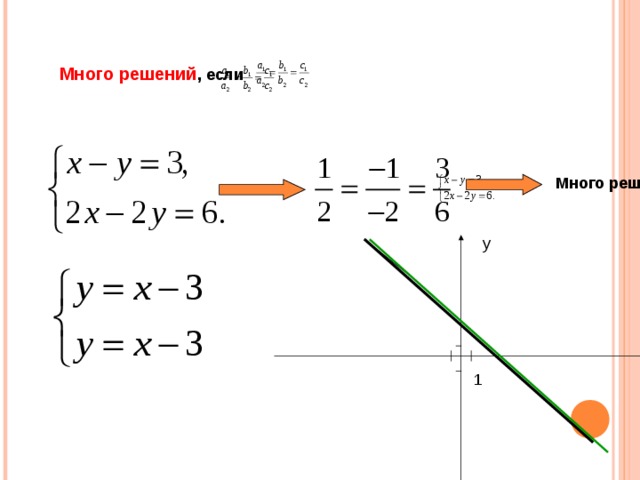
Много решений , если

Много решений

y

x

1

Проверь себя ( работа в группах)

При каком значении параметра система уравнений имеет одно решение?

При каком значении параметра система уравнений не имеет решений?

При каком значении параметра система уравнений имеет много решений?

Решение:

Система имеет много решений, если

4a-4=3a; 4a-3a=4; a=4

Значит при a=4

и

Так как

То при a =4 система имеет много решений

Итак, мы научились:

1.Решать системы линейных уравнений разными способами;

2.По виду системы отвечать на вопрос: «сколько решений имеет система»

3.А также узнали, при каком условии прямые параллельны, пересекаются.

Зачётная работа по теме: «Решение систем линейных уравнений»

• Решить систему разными способами(3балла за каждый способ)

2.Решить систему уравнений методом подбора(1 балл)

3. При всех значениях параметра a , определите число решений системы (3балла):

4.При каком значении параметра a система имеет единственное решение (2 балла):

5.При каком значении параметра a система не совместна ( 2 балла):

6.При каком значении параметра a система уравнений неопределена (2 балла):

7. Прямая y=kx+b проходит через точки A(2;7) и

B (-1;-2).Найдите значения k и b.(2 балла)

Шкала оценивания:

20б-24б --- «5» ; 13б –15б --- «4» ; 6б-9б--- «3»