Схема Бернулли и теорема Бернулли

Схема Бернулли и теорема Бернулли

10/21/24

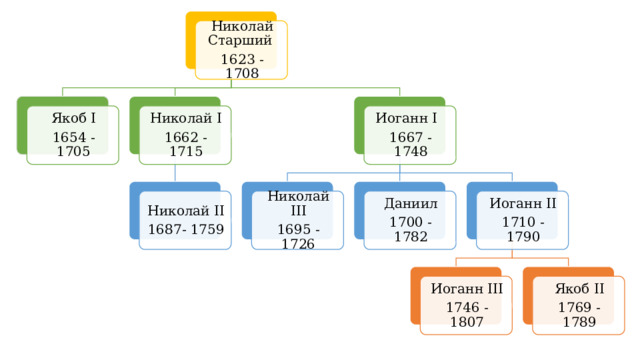
Николай Старший

1623 - 1708

Якоб I

Николай I

Иоганн I

1654 - 1705

1662 - 1715

1667 - 1748

Николай III

Иоганн II

Даниил

Николай II

1687- 1759

1710 - 1790

1695 - 1726

1700 - 1782

Иоганн III

Якоб II

1746 - 1807

1769 - 1789

Якоб Бернулли (27.12.1654 – 16.08.1705)

исследовал логарифмическую спираль

ввел полярные координаты

доказал  неравенство Бернулли

выявил  слабый закон больших чисел  (теорема Бернулли)

вычислил  число e  

изучал  процесс Бернулли

нашел решение  дифференциального уравнения Бернулли

ввел числа Бернулли

увлекался изучением теории вероятности

Формула Бернулли

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна Р , событие наступит ровно К раз, вычисляется по формуле Бернулли

где q - вероятность противоположного события

q=1-p

Какова вероятность того,

что при 10 бросаниях игрального кубика «четверка» выпадет:

а) ровно 3 раза;

б) ровно 2 раза;

в) ровно 6 раз;

г) не выпадет ни разу?

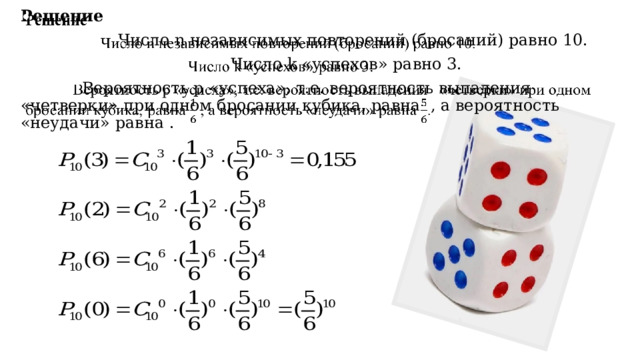
Решение

Число n независимых повторений (бросаний) равно 10.

Число k «успехов» равно 3.

Вероятность p «успеха», т.е. вероятность выпадения «четверки» при одном бросании кубика, равна , а вероятность «неудачи» равна .

Найти вероятность того, что при 9 бросаниях монеты «орел» выпадет ровно 4 раза.

Решение

Событие А выпадение «орла» , p = 0,5; q = 0,5.

Бросания предполагаем независимыми друг от друга.

По формуле Бернулли, в которой

n=9, k = 4, p = 0,5, q = 0,5.

Ответ: 0,246 .

5/16, то вероятнее выиграть одному из них 2 партии из 4-х. " width="640"

Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть одному из них 2 партии из 4-х или 3 партии из 6-ти?

Решение.

• Найдем вероятность выиграть одному из них 2 партии из 4-х:

n=4, m=2, p=1/2, q=1/2. По формуле Бернулли:

2) Найдем вероятность выиграть одному из них 3 партии из 6-ти:

n=6, m=4, p=1/2, q=1/2. По формуле Бернулли:

Сравним полученные результаты: т.к. 3/8 5/16,

то вероятнее выиграть одному из них 2 партии из 4-х.

Вероятность того, что расход электроэнергии в продолжении суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшую неделю расход электроэнергии в течении четырех суток не превысит норму.

Решение. Обозначим А – событие «расход не превысит норму».

По условию n = 7, m = 4, p = 0.75, q=1-p=0,25

По формуле Бернулли:

= 0,172536

Ответ: вероятность того, что в ближайшую неделю расход электроэнергии в течении четырех суток не превысит норму равна 0,173

За один выстрел стрелок поражает мишень с вероятностью 0,1. Найти вероятность того, что при 5 выстрелах он хотя бы раз попадет в мишень.

Решение

Считаем, что все 5 выстрелов производятся независимо друг от друга.

Событие В - попадание в мишень при одном выстреле.

p = 0,1; q = 1- 0,1 = 0,9.

А – событие, заключающееся в том, что при 5 выстрелах

будет хотя бы 1 попадание

Тогда Ā – событие, при котором стрелок все 5 раз «промазал».

Р(А) = 1- Р(Ā) =1 - 0,5905 = 0,4095

Ответ: 0,4095 .

Наивероятнейшее число появлений события.

Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных.

Решение . Вероятность изготовления бракованной детали Р = 1 - 0,8 = 0,2.

Искомые вероятности находим по формуле Бернулли:

P 5 (0) = 0,32768; P 5 (3) = 0,0512;

P 5 (1) = 0,4096; P 5 (4)=0,0064;

P 5 (2) = 0,2048; P 5 (5)=0,00032.

Полученные вероятности изобразим графически точками с координатами (m, P n (m)). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей.

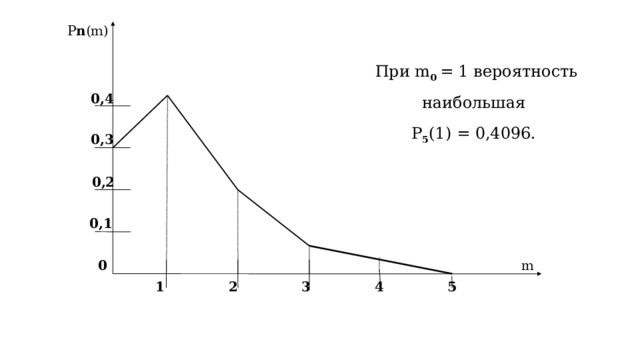
P n (m)

При m 0 = 1 вероятность наибольшая

Р 5 (1) = 0,4096.

0,4

0,3

0,2

0,1

0

m

5

4

3

2

1

Число m 0 наступления события А в n независимых испытаниях называется наивероятнейшим , если вероятность осуществления этого события Рn(m 0 ) по крайней мере не меньше вероятностей других событий Рn(m) при любом m .

Для нахождения m 0 используется двойное неравенство:

В результате многолетних наблюдений вероятность дождя 21 июля в городе N составляет 0,3. Найти наивероятнейшее число дождливых дней 21 июля на ближайшие 30 лет.

Решение. По условию: p = 0.3, q = 0.7, n = 30.

n∙p - q ≤ m 0 ≤ n∙p + p

0,3∙30 – 0.7 ≤ m 0 ≤ 0,3∙30 + 0,3

8,3 ≤ m 0 ≤ 9,3

m 0 = 9

Ответ: наивероятнейшее число дождливых дней 21 июля на ближайшие 30 лет равно 9

т.е. вероятнее всего 9 раз за 30 лет 21 июля будет дождливым.

Пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если

n = 50, m = 30, р=0,1, то для отыскания вероятности P 30 (50) надо вычислить выражение

Нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. В этом случае применяются приближённые ( асимптотические) формулы, которые позволяют приближенно найти вероятность появления события ровно m раз в n испытаниях, если число испытаний достаточно велико.

10, p0,1) . Формула Пуассона (n10, p Интегральная формула Муавра-Лапласа " width="640"

Приближённые формулы

Локальная формула

Муавра-Лапласа

(n10, p0,1) .

Формула Пуассона

(n10, p

Интегральная формула Муавра-Лапласа

10, p0,1). Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р n (m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) где " width="640"

Локальная формула

Муавра-Лапласа

(n10, p0,1).

Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность Р n (m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n)

где

5 ). " width="640"

Пользуясь этой таблицей, необходимо иметь в виду свойства функции :

1. Функция является четной, т.е.

2. Функция — монотонно убывающая при положительных значениях х, причем

при

(Практически можно считать, что уже при х 5 ).

0,1), q=1-p= = 0,2. npq = 400 ∙ 0,8∙ (1—0,8) = 64 10; . По таблице найдем " width="640"

В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти вероятность того, что из 400 семей 300 имеют холодильники.

Решение. Вероятность того, что семья имеет холодильник, равна

n = 400, m = 300, р = 80/100 = 0,8 (0,1), q=1-p= = 0,2.

npq = 400 ∙ 0,8∙ (1—0,8) = 64 10;

.

По таблице найдем

10, p Теорема. Если вероятность p наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз приближенно равна где Формулу Пуассона можно применять при λ ≤ 10. Существуют статистико-математические таблицы для распределения Пуассона. 20 " width="640"

Формула Пуассона

(n10, p

Теорема. Если вероятность p наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз приближенно равна

где

Формулу Пуассона можно применять при λ ≤ 10.

Существуют статистико-математические таблицы для распределения Пуассона.

20

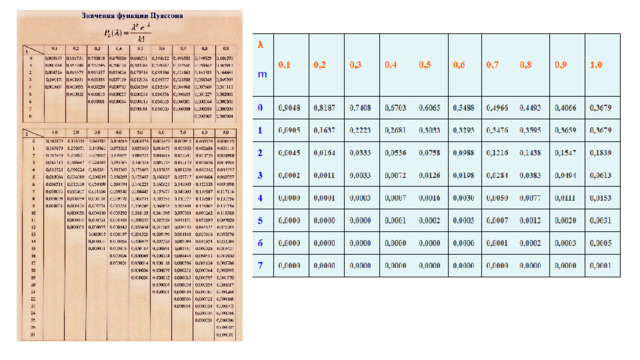
На факультете насчитывается 1825 студентов.

Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета (в году 365 дней)?

Решение. n = 1825, m=4, р = 1/365(

λ = nр = 1825 • (1/365 ) = 5

По таблицам можно точнее и быстрее найти Р(m, λ ). Так для данного примера

P 1825 (4) = P(m, λ ) = P(4,5) ≈ 0,17547.

Ответ: вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета равна 0,17547.

Интегральная формула Муавра-Лапласа

Интегральная теорема Муавра—Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n приближенно равна

где

Таблица значений функции Лапласа

26

В некоторой местности из каждых 100 семей 80 имеют холодильники. Необходимо найти вероятность того, что из 400 семей от 300 до 360 семей (включительно) имеют холодильники.

Решение. n = 400, a = 300, b = 360, р = 80/100 = 0,8, q =1-p = 0,2,

• aПо таблице: Ф (-2,5)= -Ф (2,5) ≈ -0,4938, Ф (5) ≈ 0,499997;
• a
• ; .
• По таблице: Ф (-2,5)= -Ф (2,5) ≈ -0,4938, Ф (5) ≈ 0,499997;

Тогда .

Ответ: вероятность того, что от 300 до 360 семей (включительно) имеют холодильники равна 0,993793.

= 10 " width="640"

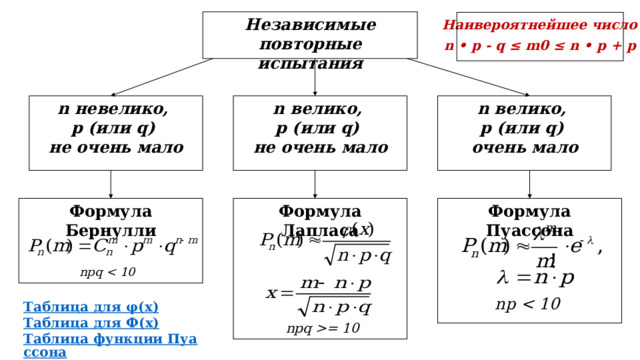
Независимые повторные испытания

Наивероятнейшее число

n • p - q ≤ m0 ≤ n • p + p

n велико,

n невелико,

n велико,

р (или q)

р (или q)

р (или q)

не очень мало

не очень мало

очень мало

Формула Пуассона

Формула Лапласа

Формула Бернулли

npq

np

Таблица для φ ( x)

Таблица для Ф( x)

Таблица функции Пуассона

npq = 10

Решение задач самостоятельно

1. Вероятность появления события А равна 0,4. Найти вероятность того, что при 6 испытаниях событие А появится не более 3 раз.

2 . Монету подбрасывают 5 раз. Найти вероятность того, что она упадет гербом не менее 4 раз.

3 . В классе 20 мальчиков и 10 девочек. На каждый из 3 вопросов, заданных учителем, ответили по одному ученику. Найти вероятность того, что среди ответивших было 2 мальчика и одна девочка.

4. По результатам проверок налоговыми инспекциями установлено, что в среднем каждое второе малое предприятие региона имеет нарушение финансовой дисциплины. Найти вероятность того, что из 1000 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины:

а) 480 предприятий;

б) наивероятнейшее число предприятий;

в) не менее 480;

г) от 480 до 520.

29

5. Вероятность малому предприятию быть банкротом за время t равна 0,2. Найти вероятность того, что из шести малых предприятий за время t сохранятся: а) два; б) более двух.

6. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета; б) не более трех пакетов.