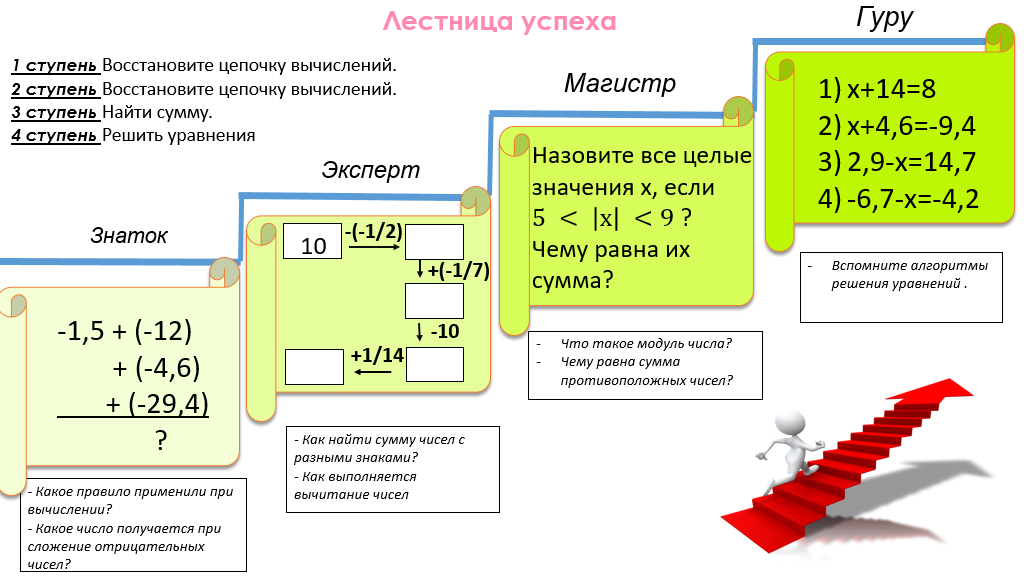
| Работа над нестандартными заданиями. Связь математики с живой природой. Сейчас мы решим несколько задач, в которых увидим, где применяются положительные и отрицательные числа. (все задачи выведены на слайды, в тетрадях записываем только решение) В биологии. Задача 1. Птица клест-еловик несет яйца и высиживает птенцов зимой. На улице температуре воздуха – 35°С, а в гнезде температура на 49°С выше. Какова температура в гнезде ? Решение. Чтобы определить температуру в гнезде , нужно 1) - 35+49= 14°С. – температура в гнезде. Ответ: 14°С.
Задача 2. Шмели выдерживают температуру до – 7,8°С, пчелы – выше этой на 1,4°С. Какую температуру выдерживают пчелы? Решение.Чтобы найти на какую температуру выдерживают пчелы, нужно к числу – 7,8 прибавить число 1,4. 1) – 7,8 + 1,4 = - 6,4 °С выдерживают пчелы. Ответ: - 6,4°С. В географии. отрицательными числами обозначают глубину морей, а положительными –высоту гор. Задача 3. Черное море имеет глубину -2500м, а Средиземное море на 3000м глубже. Какая глубина Средиземного моря? Решение: 1) -2500+(-3000)= -5500м глубина Средиземного моря. Ответ:-5500м Задача 4. Марианский желоб имеет глубину -11000м, который глубже Каспийского моря на 10000м. Какова глубина Каспийского моря? Решение: 1)-11000+10000= -1000м глубина Каспийского моря. Ответ: -1000м. В жизни. Задача 5. Если на балансе вашего телефона было 48 рублей, а ты с другом проговорил 84 рубля. Каким будет твой баланс? Мама тебе положила 100 рублей. Сколько теперь будет у тебя на счету? Решение.1)48 +(-84) = -36(р) баланс после разговора 2) – 36+100 = 64 (р) на счету Ответ: 64 рубля
Итак, где применяются отрицательные и положительные числа?
Использование знаний учащихся в стандартных условиях.
К доске приглашаются 2учащихся и записывают решение
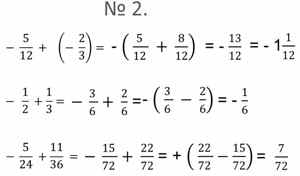
- 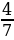 + + 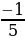 =- =- 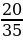 + + 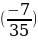 = -( = -(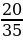 + + 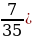 =- =- 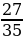
Итак, какие правила действия с дробями мы использовали?
Использование знаний учащихся в измененных условиях. Самостоятельная работа «Математическое лото». В результате выполнения этой работы, учащиеся получают два ключевых слова в изучаемой теме. На столе учеников лежат карточки с примерами и варианты ответов к ним. Учащиеся накрывают пример соответствующим ответом и получают букву угадываемого слова. Если все примеры решены правильно, то с помощью “ключа” можно отгадать слово.
| Б | Д | И | М | Н | О | Р | С | Т | У | Ь | Я | | - 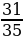 | - 2 | - 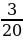 | - 1 | - 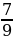 | - 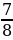 | 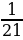
| - 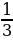 | 2 | - 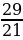 | - 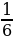 | 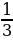
|
І вариант | № п/п | Пример | Ответ | Буква | | 1 | - 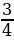 - -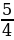 = = | - 2 | Д | | 2 | - 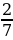 + +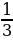 = = | 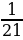
| Р | | 3 | - 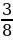 + + 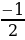 = = | - 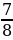 | О | | 4 | - 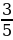 + (- + (-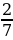 ) = ) = | - 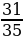 | Б | | 5 | - 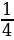 - - ) = ) = | - 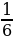 | Ь |
ІІ вариант | № п/п | Пример | Ответ | Буква | | 1 | - 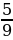 - -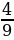 = = | - 1 | М | | 2 | - 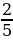 + +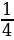 = = | - 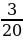 | И | | 3 | - 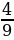 + + 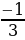 = = | - 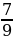 | Н | | 4 | - 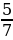 + (- + (-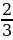 ) = ) = | - 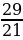 | У | | 5 | - 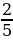 - - ) = ) = | - 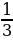 | С |
Вариант 1 – ДРОБЬ, вариант 2 – МИНУС. Так как любое рациональное число можно представить в виде дроби, то все действия с рациональными числами сводятся к действиям с дробями. И очень важно при этом соблюдать правила сложения и вычитания отрицательных чисел и чисел с разными знаками. А значит особенное внимание уделяется знаку минус. Историческая пауза. Два ученика выступают с сообщениями о возникновении дробей и о происхождении отрицательных чисел. «Не зная прошлого развития науки, трудно понять ее настоящее». Историческая «дробная» пауза. Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби. Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась “асс”. 12-ую долю “асса” называли унцией, а сами дроби - двенадцатеричными. В древнем Вавилоне предпочитали наоборот - постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. На Руси дроби называли долями, позднее “ломаными числами”. Современное обозначение дробей берет начало в Древней Индии. Вначале в записи дробей не использовалась дробная черта. Горизонтальную черту, одним из первых применял таджикский ученый ал – Насави, который умер около 1030 г. Автором первого европейского учебника, в котором использовалась современная запись дробей итальянский купец и путешественник Кибоначчи Леонардо Пизанский, который путешествуя по Востоку, познакомился с достижениями арабской математики; способствовал передаче их на Запад, применял эту черту регулярно, после него дробная черта вошла в обиход. Название числитель и знаменатель ввел в XIII в. Максим Пеануд-греческий – монах, учитель-математик.
Историческая пауза. Когда и где появились отрицательные числа? Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. Ни египтяне, ни вавилоны, ни даже древние греки чисел этих не знали. Впервые с отрицательными числами столкнулись китайские ученые в связи с решением уравнений. Они уже умели их складывать и вычитать. Однако знаки “ + “ или “ – “ тогда не употребляли, а изображали положительные числа красным цветом, а отрицательные – черным, называя их “фу”. Индийские математики Брамагупта (VII век) и Бхаскара (XII век) представляли себе положительные числа как «имущества», а отрицательные числа как «долги». Они составили правила действий для этих чисел. Вот как индийский математик Брамагупта (VIIв.) излагал правила сложения и вычитания: «Сумма двух имуществ есть имущество», «Сумма двух долгов есть долг», «Сумма имущества и долга равна их разности» и т.д. Однако долгое время отрицательные числа считали не настоящими, фиктивными, абсурдными. В Европе отрицательными числами начали пользоваться с XII –XIII вв., но до XVI.в., как и в древности, они понимались как долги, большинство учёных считали их «ложными» в отличие от положительных чисел – «истинных». Признанию отрицательных чисел способствовали работы французского математика, физика и философа Рене Декарта (1596 – 1658). Он предложил геометрическое истолкование положительных и отрицательных чисел – ввел координатную прямую в 1637 году. Спасибо , конечно, Не зная прошлого развития науки, трудно понять ее настоящее».
Занимательная задача «Найти сумму всех целых чисел от – 499 до 501». Учитель предложил Незнайке решить дома следующее задание: «Найти сумму всех целых чисел от - 499 до 501». Незнайка как обычно сел за работу, однако дело шло медленно. Тогда на помощь ему пришли мама, папа, бабушка. Вычисляли, пока от усталости не стали смыкаться глаза. А вы, ребята, как бы решили такое задание? Нашли значение следующего выражения – 499 + (– 498) + (– 497) + …+ 497 + 498+ 499 + 500 + 501? Вспомогательные вопросы к задаче Какими числами являются некоторые слагаемые? Чему равна сумма противоположных чисел? Какие свойства сложения можно применить? Решение. Так как сумма противоположных чисел равна 0, то – 499 + (– 498) + (– 497) + …+ 497 + 498+ 499 + 500 + 501 = = 501 + 500 + (– 499 + 499) + (– 498 + 498) + (– 497 + 497) + …+ (– 1 + 1) + 0 = = 501 + 500 + 0 = 1001. Ответ: сумма всех целых чисел от – 499 до 501 равна 1001.
Блицтурнир учитель против 6-Б класса. Верно ли утверждение: 1) сумма двух чисел с разными знаками всегда положительна; 2) сумма двух чисел с разными знаками не всегда положительна; 3) сумма двух чисел с разными знаками всегда отрицательна; 4) сумма двух чисел с разными знаками не всегда отрицательна; 5) сумма двух чисел с разными знаками всегда равна нулю; 6) сумма двух чисел с разными знаками может быть равна нулю; 7) знак суммы двух чисел с разными знаками всегда такой же, как у слагаемого с большим модулем; 8) если модули слагаемых с разными знаками равны, то сумма слагаемых равна нулю; 9) модуль суммы двух чисел с разными знаками равен сумме модулей слагаемых; 10) модуль суммы отрицательных чисел равен сумме модулей слагаемых; 11) сумма отрицательных чисел всегда отрицательное число.
Рефлексия. А теперь давайте вернемся к задаче, которую я вам зачитала в начале урока. В чем же ее смысл? - А что же нового вы узнали сегодня на уроке? - Довольны ли вы результатами? - Что понравилось в работе? - Какие трудности испытывали? - Как их преодолевали? - Покажите, какое настроение сейчас у вас.
9. Подведение итогов урока. Выставление оценок.
Задание на карточке: В клетки квадрата записать такие числа, чтобы сумма чисел по любой вертикали, горизонтали была равна 0 Ответ: | -3 | -5,3 | 8,3 | | 2,5 | 4,4 | -6,9 | | 0,5 | 0,9 | -1,4 |
2 препятствие . Тот, кто не знает математики , не может узнать никакой другой науки. (Роджер Бэкон) Устный счет. 1) 15 – (- 58) = 4) 28 – 100 = 7) 75 – 90 = 2) – 36 – 24 = 5) – 20 + 6 = 6) – 75 + 75 = 9) -35 – 28 =
3 препятствие . Математика – точильный камень способностей. Работа в тетрадях. 1. Упростите сумму: -8+х+(-22). 2. Упростите сумму: -10+а+34. 3. Разность у и 6 равна 12. Найдите у. 4. Решите уравнение: 5-с=12. ). Самое маленькое государство – Ватикан – 189 + 233 =? (44 гектара) в). Материк с наибольшим числом границ – Африка – 75 +? = 33 (108) МИР построен на силе ЧИСЕЛ. (Пифагор) а) Математические знаки. 1). *6 *18 =-14 2). *29 * 50=+21 б) Какая рыба без чешуи? 1) Щука-5 2) Сом-7, 3) Карась-9. –15+у=-8 в) Какое озеро самое красивое? 1)Чудское-2 2) Ильмень-4, 3)Байкал-6. m+(-14)=-8
| 





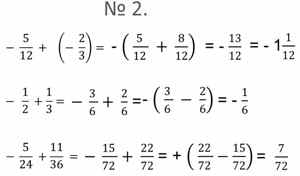
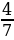 +
+ 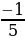 =-
=- 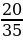 +
+ 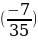 = -(
= -(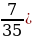 =-
=- 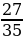
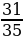
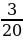
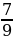
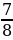
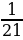
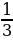
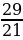
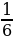
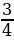 -
-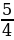 =
=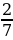 +
+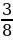 +
+ 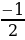 =
=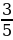 + (-
+ (-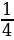 -
- ) =
) =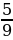 -
-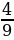 =
=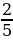 +
+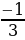 =
=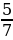 + (-
+ (-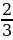 ) =
) =