Сложение и вычитание векторов.
Сумма двух векторов. Законы сложения векторов. Правило параллелограмма.
Представим себе такую ситуацию. Направляясь из школы домой, вам захотелось пить и вы решили зайти сначала в магазин, а затем уже домой. Цель достигнута: вы из школы добрались домой. Сейчас мы описали принцип первого правила сложения векторов.
Правило треугольника.
Чтобы найти вектор суммы двух векторов  и
и 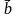 , нужно:
, нужно:
-
совместить параллельным переносом начало вектора 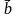 с концом вектора
с концом вектора  ;
;
-
провести вектор из начала вектора  в конец вектора
в конец вектора 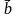 ;
;
-
получившийся вектор и есть вектор суммы: 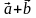 .
.

Если к вектору  прибавить нулевой вектор
прибавить нулевой вектор 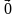 по правилу треугольника, то получим вектор
по правилу треугольника, то получим вектор  , т.е. справедливо равенство:
, т.е. справедливо равенство: 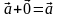 .
.
Утверждение. Если  и
и 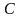 – произвольные точки, то
– произвольные точки, то 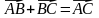 .
.
Например, 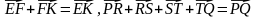 .
.
Сложение векторов подчиняется алгебраическим законам.
ТЕОРЕМА. Для любых векторов 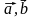 и
и  справедливы равенства:
справедливы равенства:
 (переместительный закон)
(переместительный закон)
 (сочетательный закон).
(сочетательный закон).
Дано: 
Доказать: 1) 
2) 
Доказательство.
Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны.
1). Отметим произвольную точку 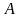 и отложим от этой точки вектор
и отложим от этой точки вектор  . Воспользуемся правилом треугольника и прибавим к нему вектор
. Воспользуемся правилом треугольника и прибавим к нему вектор  . Вектором суммы этих двух векторов является вектор
. Вектором суммы этих двух векторов является вектор  . (Рисунок слева).
. (Рисунок слева).
Теперь от точки 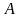 и отложим вектор
и отложим вектор  . По правилу треугольника прибавим к нему вектор
. По правилу треугольника прибавим к нему вектор  . Вектором суммы этих двух векторов является вектор
. Вектором суммы этих двух векторов является вектор  . (Рисунок справа).
. (Рисунок справа).
– параллелограмм и точка  совпадает с точкой
совпадает с точкой 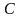 . Значит,
. Значит,  , т.е.
, т.е. 
2
). От точки 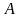 отложим вектор
отложим вектор  , от точки
, от точки  отложим вектор
отложим вектор  , а от точки
, а от точки 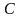 – вектор
– вектор  . Найдём суммы векторов по правилу треугольника.
. Найдём суммы векторов по правилу треугольника.
Теорема доказана.
При доказательстве первой формулы получился параллелограмм, причём, из точки 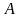 выходят два вектора
выходят два вектора  и
и 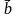 , а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.
, а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов.
Правило параллелограмма.
Чтобы найти вектор суммы двух векторов  и
и 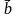 , нужно:
, нужно:
-
совместить параллельным переносом начала векторов  и
и 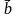 ;
;
-
на этих векторах достроить параллелограмм;
-
вектором суммы 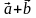 является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.
является вектор, который лежит на диагонали параллелограмма, имеющий своё начало в начале исходных векторов.
Сумма нескольких векторов.
Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример.
Сложить векторы  .
.
О тметим точку  и отложим от неё вектор
и отложим от неё вектор  . Прибавим к нему вектор
. Прибавим к нему вектор  по правилу треугольника.
по правилу треугольника. 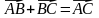 . Теперь к вектору
. Теперь к вектору  прибавим вектор
прибавим вектор  .
.  . К вектору
. К вектору  прибавляем вектор
прибавляем вектор  .
.  . Осталось к вектору
. Осталось к вектору  прибавить вектор
прибавить вектор  .
.  .
.
Итак, . Значит, суммой векторов  является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.
является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника.
Правило многоугольника.
Чтобы найти вектор суммы нескольких векторов, нужно:
-
последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего;
-
вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего.
Вычитание векторов.
Определение. Разностью двух векторов  и
и 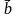 называется такой вектор
называется такой вектор  , что при сложении его с вектором
, что при сложении его с вектором 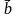 получается вектор
получается вектор  .
.

В ычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них.
Сложим векторы  и
и 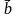 по правилу треугольника. По рисунку видно, что
по правилу треугольника. По рисунку видно, что 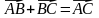 . Отсюда,
. Отсюда,  и
и  . Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:
. Значит, разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила:
I правило вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
-
совместить параллельным переносом начала этих векторов;
-
вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора.

II правило вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно:
-
совместить параллельным переносом концы этих векторов;
-
вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора.

Далее, из алгебры мы знаем, что для того, чтобы из числа  вычесть число
вычесть число  , нужно к числу
, нужно к числу  прибавить число, противоположное числу
прибавить число, противоположное числу  , т.е.
, т.е.  . Такое же правило справедливо и для векторов.
. Такое же правило справедливо и для векторов.
ТЕОРЕМА. Для любых векторов 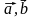 справедливо равенство:
справедливо равенство:

Дано: 
Доказать:
Доказательство.
1. Найдём разность векторов  по I правилу. Вектором разности является вектор
по I правилу. Вектором разности является вектор  (рисунок слева). А теперь найдём сумму векторов
(рисунок слева). А теперь найдём сумму векторов  по правилу треугольника, где
по правилу треугольника, где  – вектор, противоположный вектору
– вектор, противоположный вектору 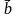 . Вектором суммы является вектор
. Вектором суммы является вектор  (рисунок справа). Не трудно заметить, что
(рисунок справа). Не трудно заметить, что  . Они сонаправлены и имеют одинаковые модули.
. Они сонаправлены и имеют одинаковые модули.
2. А теперь докажем то же самое аналитически. По определению разности векторов,




Что и требовалось доказать.
Из этой теоремы следует третье правило вычитания векторов.
III правило вычитания векторов.
Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму.
Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно.
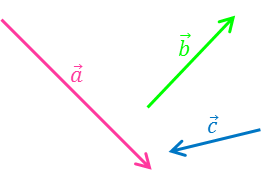
-
В ектор  является суммой векторов
является суммой векторов  и
и 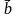 . Определите, какой из четырёх рисунков верный.
. Определите, какой из четырёх рисунков верный.
-
Проведите векторы . Какая геометрическая фигура у вас получилась?
-
В ектор  является разностью векторов
является разностью векторов  и
и 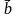 . Определите, какой из четырёх рисунков верный.
. Определите, какой из четырёх рисунков верный.
-
В ектор  является суммой векторов
является суммой векторов  и
и 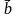 . Определите, какой из четырёх рисунков верный.
. Определите, какой из четырёх рисунков верный.
-
В ыразите вектор  через векторы
через векторы  , используя рисунок.
, используя рисунок.
-
В ыразите вектор  через векторы
через векторы  , используя рисунок.
, используя рисунок.
-
Упростите выражения:
-
Длина вектора  равна
равна  , а длина вектора
, а длина вектора  равна
равна  . Сколько различных целых значений может принимать длина вектора
. Сколько различных целых значений может принимать длина вектора  ?
?
-
Длина вектора  равна
равна  , а длина вектора
, а длина вектора  равна
равна  . Сколько различных целых значений может принимать длина вектора
. Сколько различных целых значений может принимать длина вектора  ?
?
-
Длина вектора  равна
равна  , а длина вектора
, а длина вектора  равна
равна  . Сколько различных целых значений может принимать длина вектора
. Сколько различных целых значений может принимать длина вектора  ?
?
-
Длина вектора  равна
равна  , а длина вектора
, а длина вектора  равна
равна  . Сколько различных целых значений может принимать длина вектора
. Сколько различных целых значений может принимать длина вектора  ?
?
-
Длина вектора  равна
равна  , а длина вектора
, а длина вектора  равна
равна  . Сколько различных целых значений может принимать длина вектора
. Сколько различных целых значений может принимать длина вектора  ?
?
-
В квадрате  проведены диагонали
проведены диагонали  и
и  . Укажите номера верных утверждений.
. Укажите номера верных утверждений.
-
 – параллелограмм. Найдите сумму векторов .
– параллелограмм. Найдите сумму векторов .
-
 – прямоугольник. Диагонали
– прямоугольник. Диагонали  и
и  пересекаются в точке
пересекаются в точке  . Укажите номера верных утверждений.
. Укажите номера верных утверждений.
-
 – параллелограмм. Выразите векторы
– параллелограмм. Выразите векторы  и
и  через векторы
через векторы  и
и  .
.
-
 – параллелограмм. Выразите векторы
– параллелограмм. Выразите векторы  и
и  через векторы
через векторы  и
и 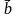 .
.
-
 – прямоугольник. Выразите векторы
– прямоугольник. Выразите векторы  и
и  через векторы
через векторы  и
и  .
.
-
 – параллелограмм. Выразите векторы
– параллелограмм. Выразите векторы  и
и  через векторы
через векторы  и
и 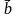 .
.
-
Н айдите длины векторов  , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
, изображённых на клетчатой бумаге с размерами клетки 1 х 1.
-
Д ве стороны прямоугольника  равны 20 и 21. Найдите длину суммы векторов
равны 20 и 21. Найдите длину суммы векторов  и
и  .
.
-
Д ве стороны прямоугольника  равны 7 и 24. Найдите длину разности векторов
равны 7 и 24. Найдите длину разности векторов  и
и  .
.
-
Н а каждом рисунке найдите длину вектора  (размеры клетки 1 х 1).
(размеры клетки 1 х 1).
-
Н а каждом рисунке найдите длину суммы векторов  и
и 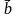 (размеры клетки 1 х 1).
(размеры клетки 1 х 1).
-
Н а каждом рисунке найдите длину разности векторов  и
и 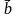 , изображённых на клетчатой бумаге с размерами клетки 1 х 1.
, изображённых на клетчатой бумаге с размерами клетки 1 х 1.
5







 и
и 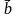 , нужно:
, нужно: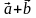 .
.
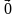 по правилу треугольника, то получим вектор
по правилу треугольника, то получим вектор 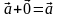 .
. и
и 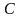 – произвольные точки, то
– произвольные точки, то 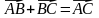 .
. 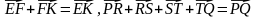 .
. и
и  справедливы равенства:
справедливы равенства: (переместительный закон)
(переместительный закон) (сочетательный закон).
(сочетательный закон).

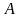 и отложим от этой точки вектор
и отложим от этой точки вектор 

















