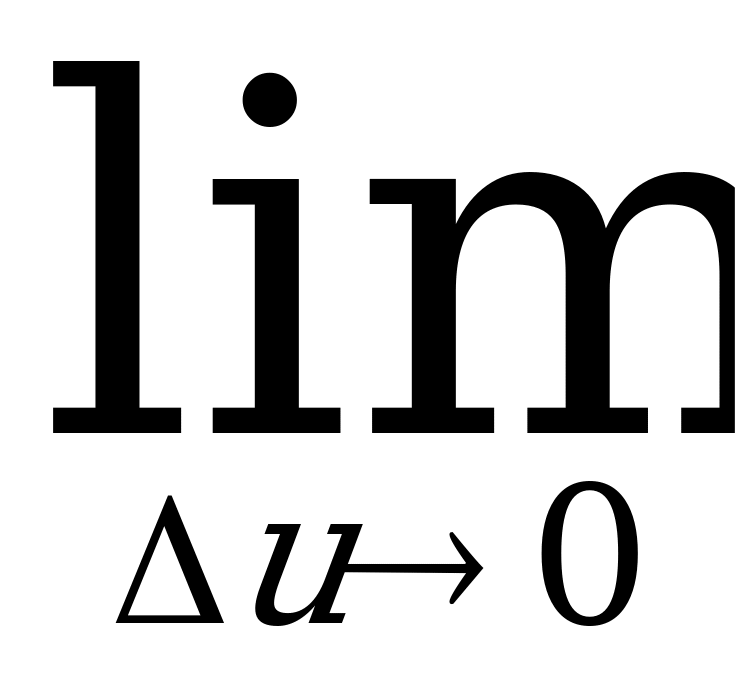Урок по алгебре в 11 классе.
Тема: Сложная функция и ее производная.
Цели:
-
ввести понятие сложной функции, ознакомить с выведением правила дифференцирования сложной функции;
-
научить представлять сложные функции в виде композиций элементарных функций, учить распознавать сложные функции;
-
продолжать прививать интерес к предмету, расширять кругозор учащихся, демонстрировать межпредметные связи;
-
воспитывать добросовестное отношение к учебе, формировать умение аккуратно вести записи, самостоятельно работать с литературой.
Оборудование: опорный конспект по теме «Производная», плакаты, две матрешки, модель куба и трехгранного угла, графики функций.
Ход урока.
І. Введение. Активизация внимания.
1. На доске плакат:






Вы видите трехгранный угол и коробку. Присмотритесь повнимательнее, где расположена коробка - внутри угла или вне его?
Большинству из вас кажется, что коробка находится внутри. Но при желании можно увидеть и другое положение, будто нижняя грань угла «отогнута», и коробка расположена снаружи. (Учитель показывает на модели)
2. Рассмотрим расположение двух матрешек, вложенных одна в другую. Если в случае с коробкой игра была построена на основе оптических иллюзий, то сейчас достаточно открыть одну куклу и посмотреть, есть ли внутри другая или нет.
3. На доске запись: у=
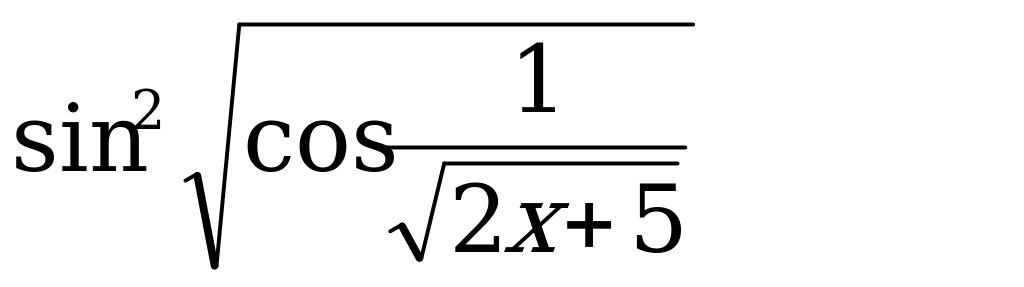
Определите порядок вычислений значения данного выражения при заданном х .
Не случайно мы рассмотрели эти три примера, на первый взгляд не связанных между собой. Но одна связь все же есть: вложенность. Будучи вложенными одна фигура или функция в другую, образовалась композиция, которая и создала более сложную ситуацию. И сегодня на уроке нам предстоит окунуться в мир сложной функции и ее производной.
Историческая справка.
Великий астроном древности Птолемей, чтобы объяснить движение планет по небу, придумал сложную систему мироздания, в которой было такое нагромождение окружностей ( планетных орбит), что когда королю Альфонсу Х пытались объяснить систему, он сказал: «Жаль, что меня не было, когда бог творил мир: я посоветовал бы ему сделать мироздание проще».
Но мы не станем поддерживать это заявление, дабы нас не обвинили в богохульстве (что, кстати, произошло с Альфонсом Х и чуть не лишило его короны). А наоборот, увидим как мир красив в своем многообразии, как удивительно красивы сложные фукции и по своей структуре, и в применении к различным областям знаний.
ІІ. Актуализация опорных знаний.
Начнем мы пока с простого и известного.
Задание: Предлагается набор графиков. Составить пары «функция - ее производная». (рисунок 1) Ответы: (1г; 2а; 3в; 4б; 5д.)
Заметим, что сейчас мы вспомнили некоторые элементарные функции и их производные. К элементарным также относятся тригонометрические функции, им обратные, показательная и логарифмическая. А сейчас посмотрим, как с их помощью образуются сложные функции.
ІІІ. Объяснение первой части нового материала.
Со сложными функциями мы уже встречались, когда преобразовывали графики, находили области определения. Помните, у=sin 2x, у=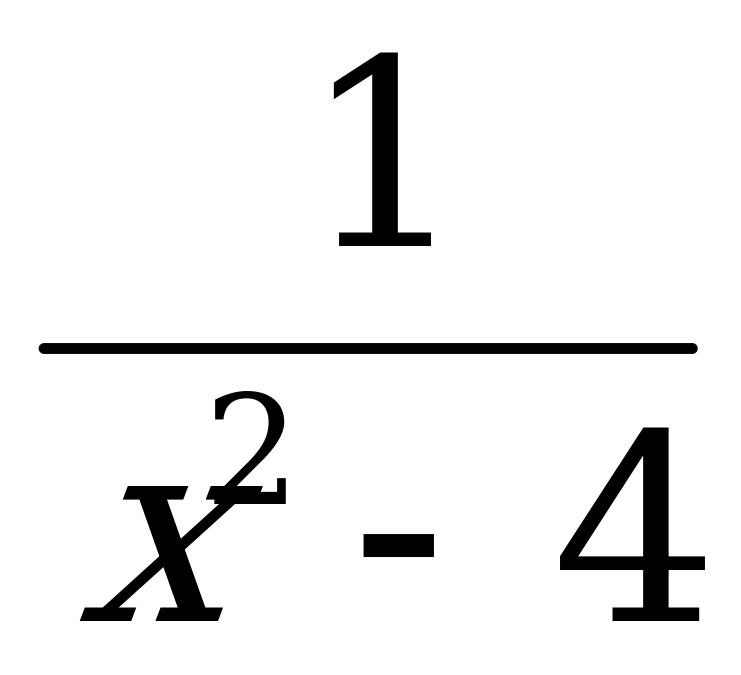 ? Рассмотрим график фукции у=
? Рассмотрим график фукции у=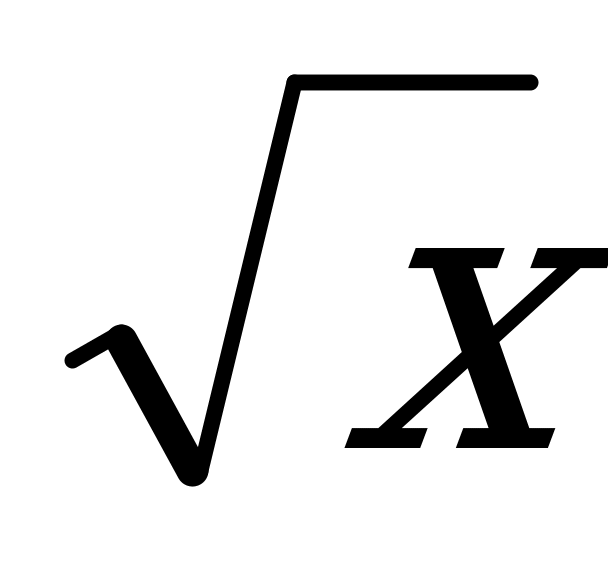 . Если изменить подкоренное выражение , то получится другая функция, например у=
. Если изменить подкоренное выражение , то получится другая функция, например у=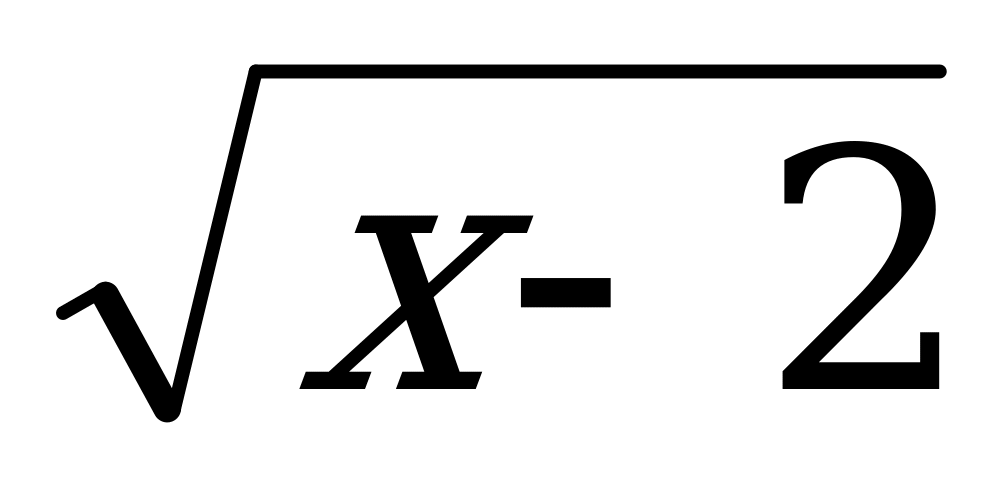 , соответственно и другой график , хотя по форме он похож на у=
, соответственно и другой график , хотя по форме он похож на у=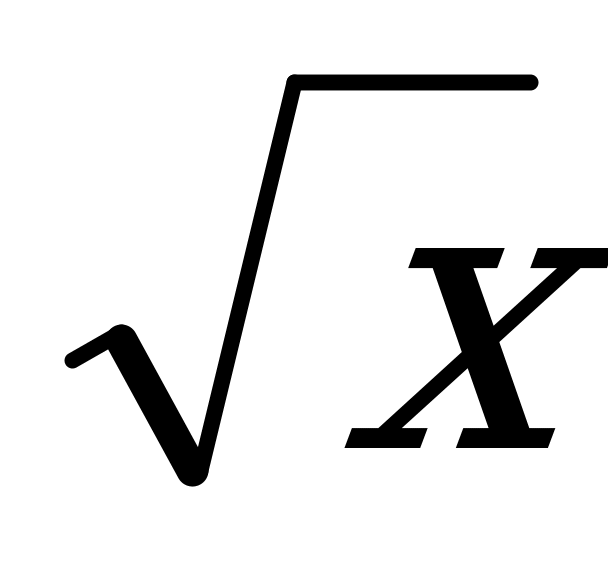 . (показываем на модели).
. (показываем на модели).
Как найти значение этой функции в фиксированной точке х ? Для этого нужно: 1) вычислитьзначение выражения х-2 (записываем на доске); 2) найти значение корня из полученного числа. Иными словами, сначала нужно найти значение функции g(х)=х-2, а потом найти значение функции f=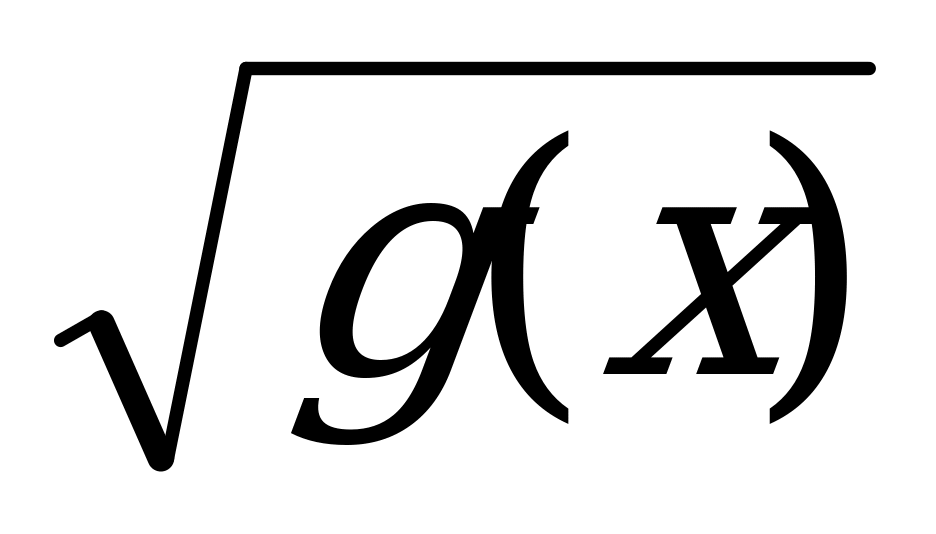 , которая сама по себе является функцией. В подобных случаях говорят, что задана сложная функция f (g(х)).
, которая сама по себе является функцией. В подобных случаях говорят, что задана сложная функция f (g(х)).
В нашем примере (записываем на доске) f(u)=
нашем примере (записываем на доске) f(u)= 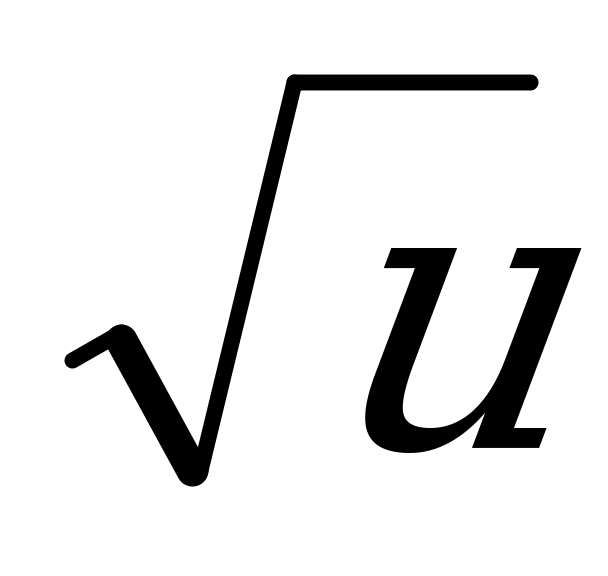 где и= g(х)=х-2. Переменную и называют внутренней переменной или промежуточной (соответственно, внутренней или промежуточной функцией), а f(и) называют внешней функцией. Таким образом: (записываем в тетрадь)
где и= g(х)=х-2. Переменную и называют внутренней переменной или промежуточной (соответственно, внутренней или промежуточной функцией), а f(и) называют внешней функцией. Таким образом: (записываем в тетрадь)
 у = f ( g (х) ) - сложная функция
у = f ( g (х) ) - сложная функция
основная переменная
промежуточная переменная (внутренняя)
внешняя функция
ІV. Закрепление материала.
Часть 1.
Вернемся к функции из первой части урока: у=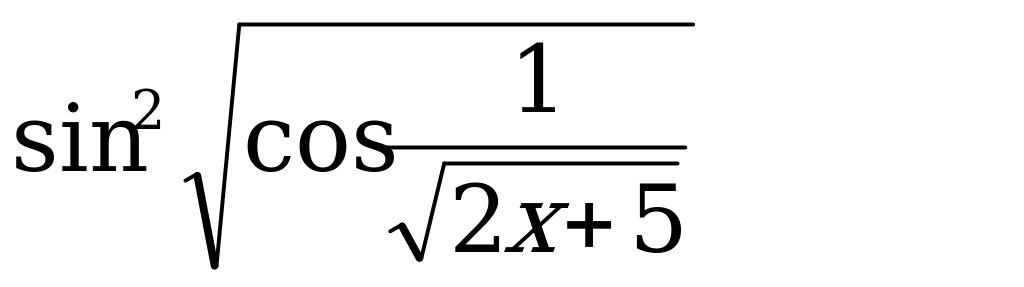
Задание к классу:
-
Из каких элементарных функций составлена эта функция?
-
Сколько всего элементарных функций задействовано в построении этой функции? ( Семь)
-
Запишите эти элементарные функции. (два ученика работают у доски)
-
Эта сложная функция является квадратичной или тригонометрической ? (Квадратичной)
-
Чем является для сложной функции функция у=sin х ? (Промежуточной переменной)
-
Как это определить? (Порядком действий)
Часть ІІ.
Можно ли сказать, что сложная функция - это функция от функции? (Да)
Когда математик употребляет понятие «сложная функции», он подразумевает, что эта функция есть результат операции последовательного выполнения некоторых функций (что мы сейчас и увидели) . Эту операцию называют композицией (видите, какой музыкальный термин использовали математики?).
Является ли сложной функция g(х)=sin x . cos x? (Нет, т.к. это не функция от функции, а произведение двух различных функций).
Ваша задача: научиться распознавать сложные функции, уметь определять промежуточную переменную, представлять сложные функции в виде композиций элементарных функций.
Устные упражнения.
-
Укажите номера сложных функций:
| 1) у = (х+3)4 2) у = аrсsin х 3) у =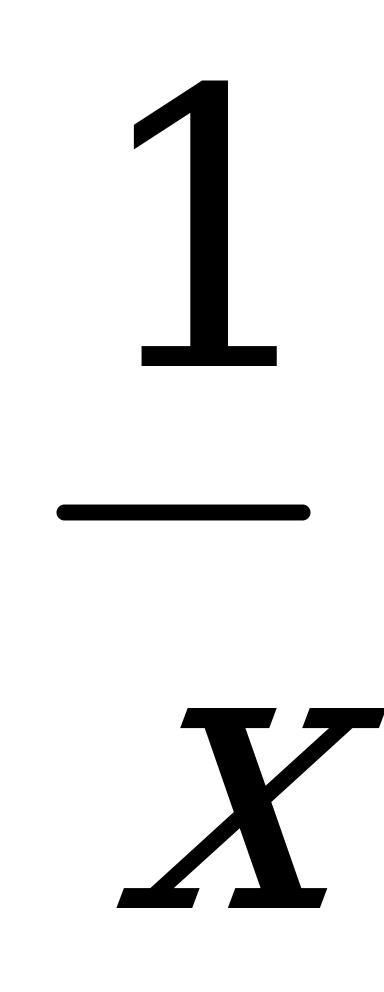 +1 +1 | 4) у = 2 sin х соs х 5) у = 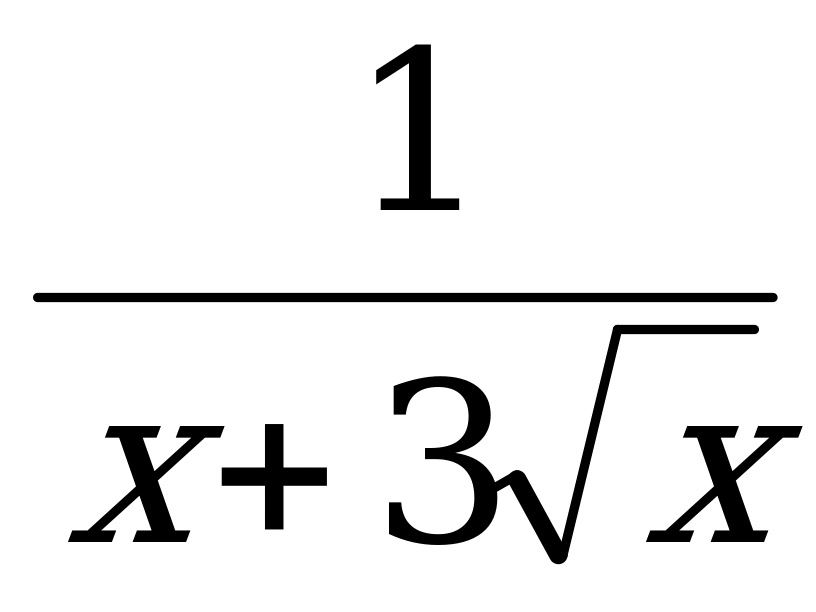 6) у = х2 . | х | | 7) у=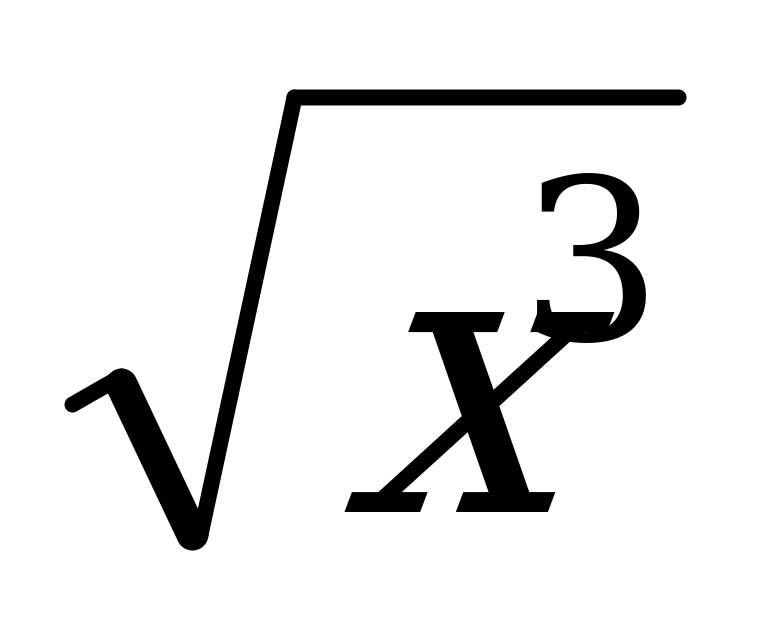 8) у= sin 2х 9) у= х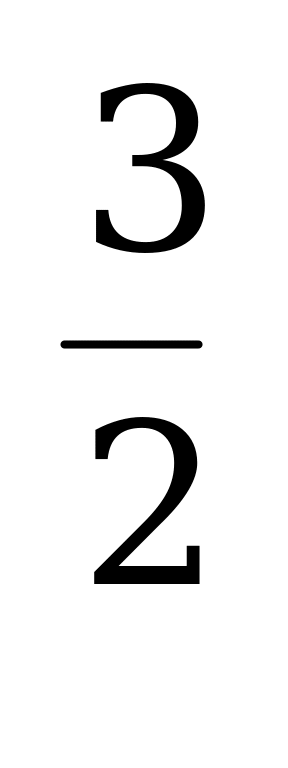 |
(1, 5, 7, 8 )
2. Под какими номерами находятся функции, для которых можно применить правила вычисления производных? (2, 3, 4, 6, 9).
3. Есть ли среди данных функций те, значения которых во всех точках х равны? (Да, 4 и 8) Обратите внимание, правые части функций 4) и 8) тождественно равны. Это одна и та же функция! Но в записи у= sin 2х она сложная. Т.е. «сложная функция» - это форма записи функции.
4. Есть ли еще такая же ситуация? (Да, 7 и 9) Как можно иначе представить эти функции ? (х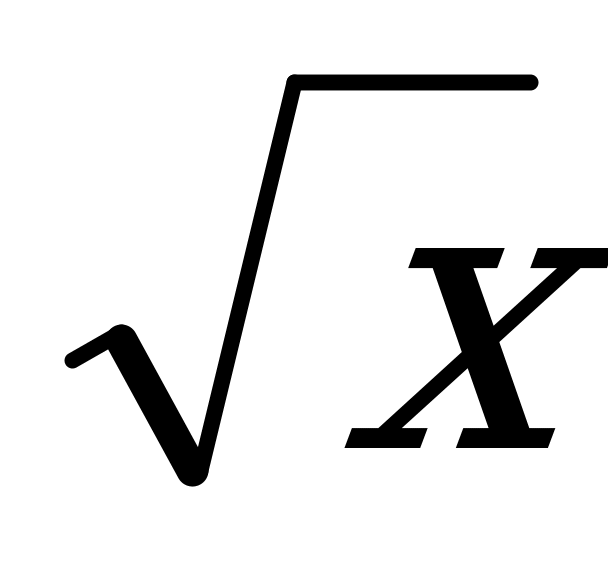 )
)
Ясно, что у тождественных функций производные будут равны.
Упражнение:
Заданы функции: с(х)=х/(х-1) ; р(х)= соs х ; у(х)= 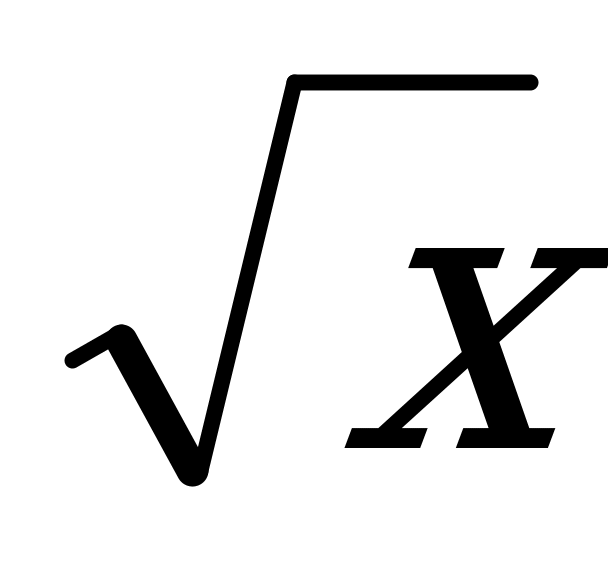
Составьте следующие композиции:
1) с(р(х)); 2) р(с(х)) ; 3) с(у(х)) ; 4) у(с(х)) ; 5) р(у(х)) ; 6) у(р(х)) ;
7) у(у(х)); 8)* с(с (у (р (у(х))))).
Н а доске показан образец записи решения:
а доске показан образец записи решения:
-
с(р(х)) - ?
U= р(х)= соs х
с(р(х)) = с(U) = 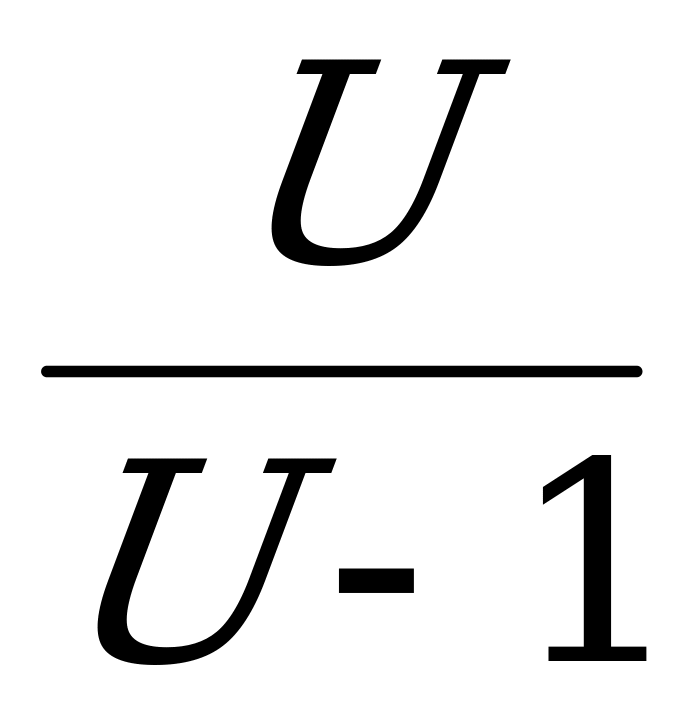 =
= 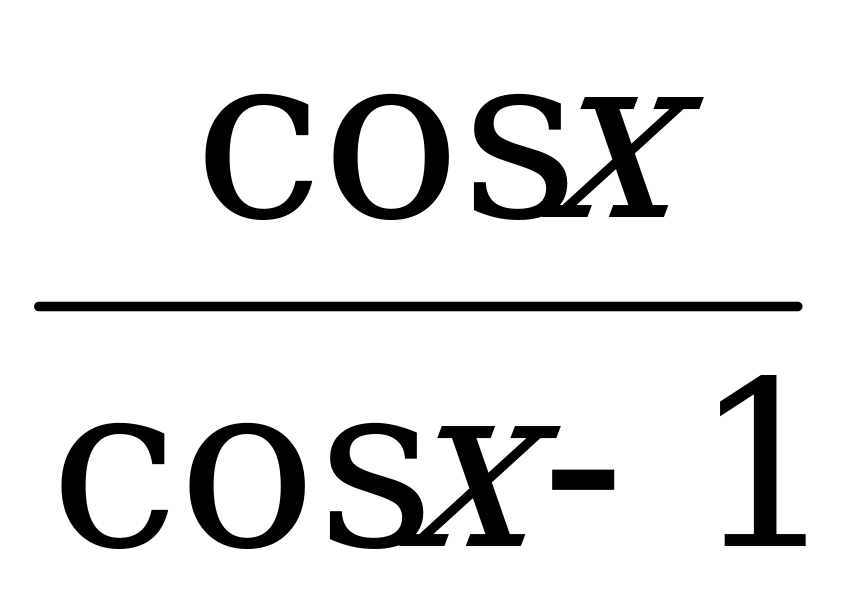
Обратите внимание: внешняя функция придает «форму» выражению, а внутренняя - «содержание»! Используя это мнемоническое правило, вы можете быстро ориентироваться в любых композициях.
Учащиеся начинают работать в парах, по одному желающему выходят к доске, записывают ответы:
1) 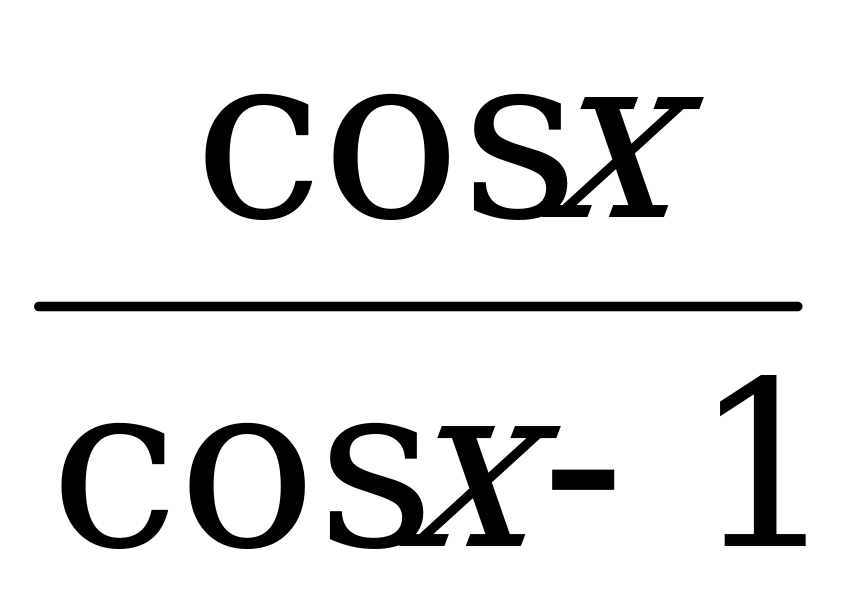 ; 2)
; 2) 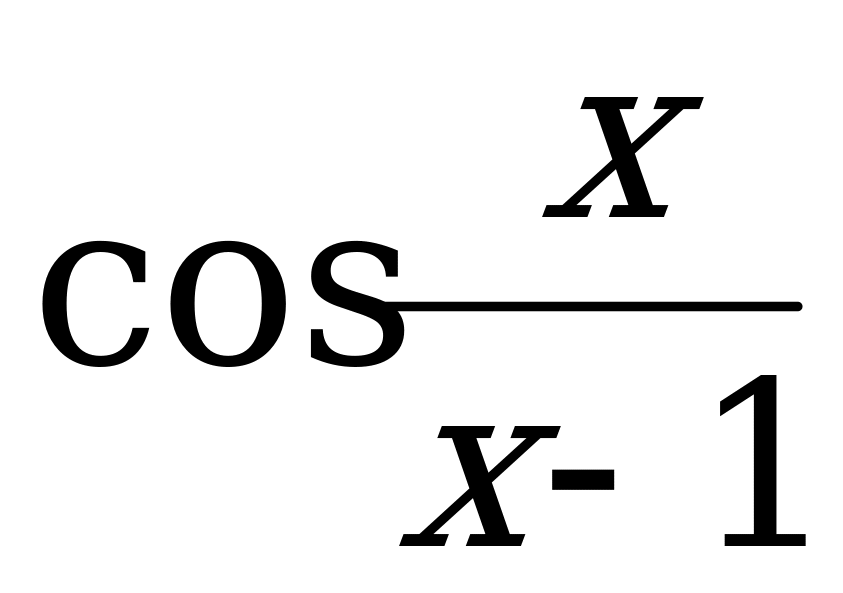 ; 3)
; 3)  ; 4)
; 4) 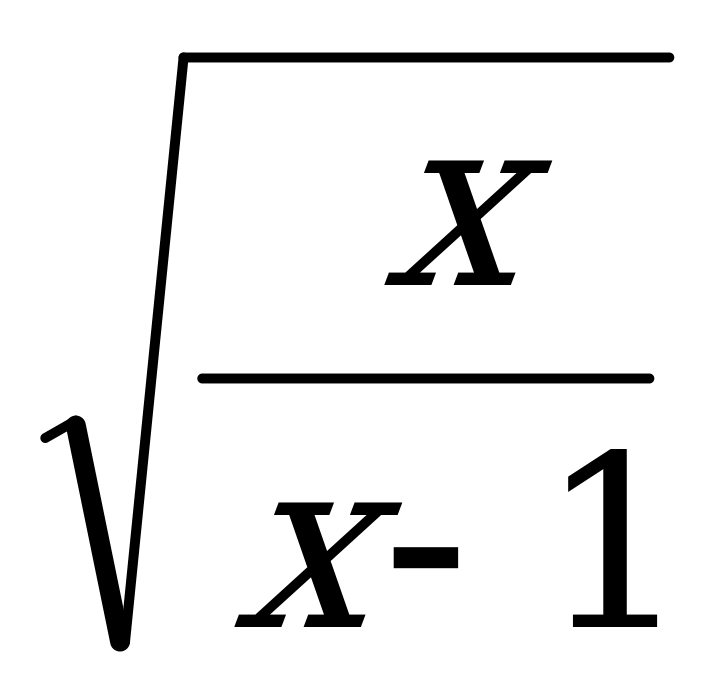 ; 5) cos
; 5) cos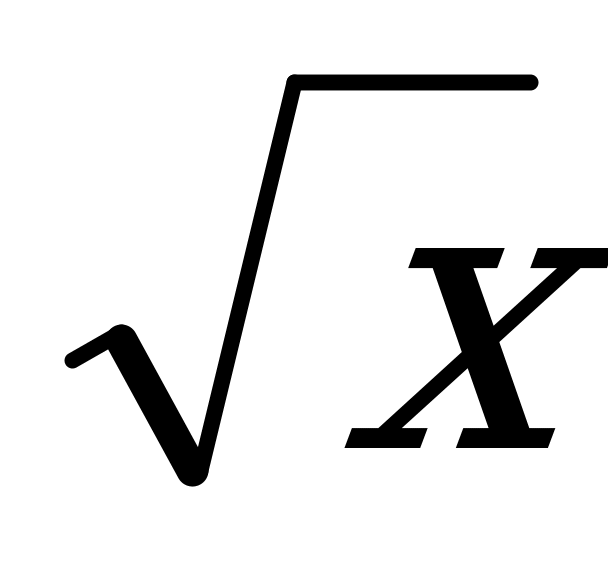 ; 6)
; 6) 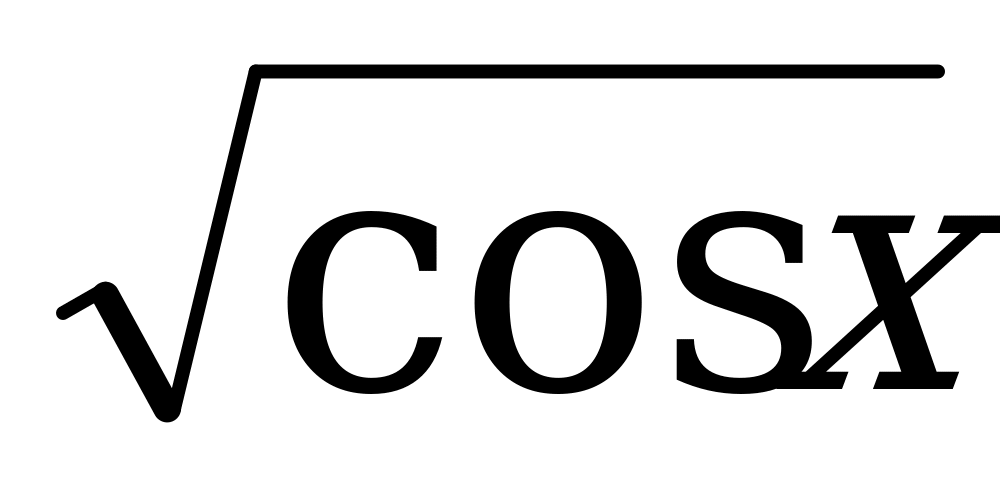 ; 7)
; 7) 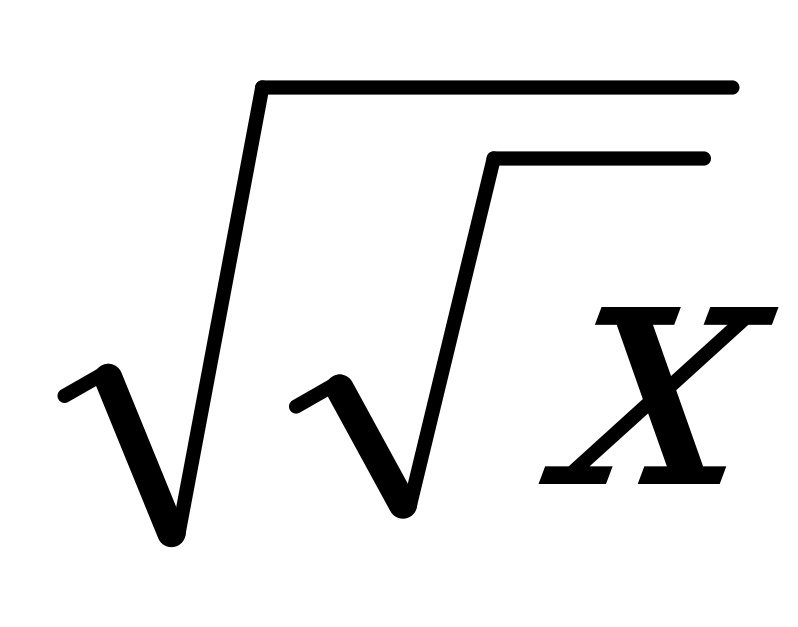 или
или 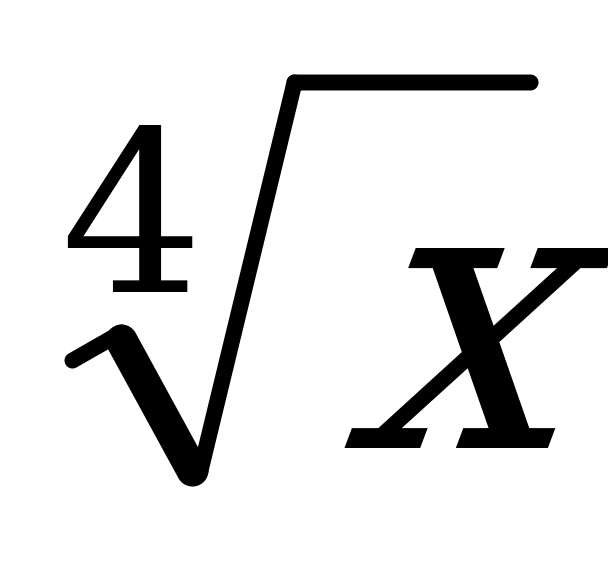 .
.
Можно ли сказать, что композиции 1 и 2 равносильны? (Нет)
Какой композицией можно записать функцию под номером 8*? ( у(р(у(х))) )
Часть ІІІ.
Предлагается доклад учащегося о том, на службе у каких наук и отраслей находятся сложные функции:
«Сложные функции находят широкое применение в различных областях.
А) Например, в атомной физике применяется формула m(t) = M (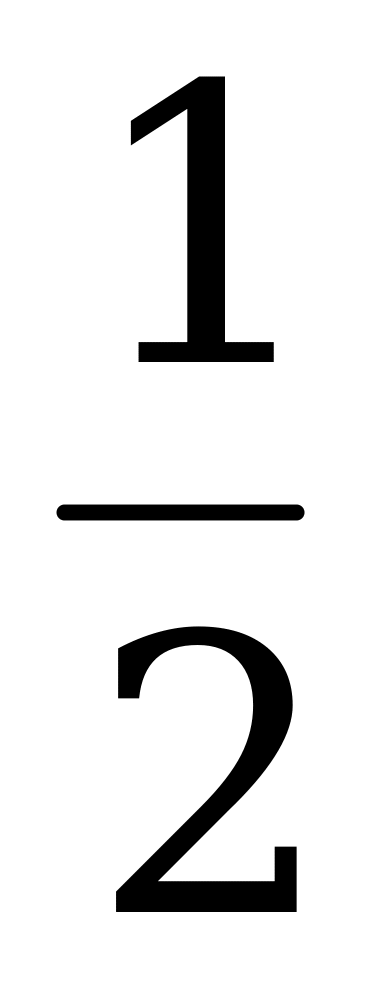 )
)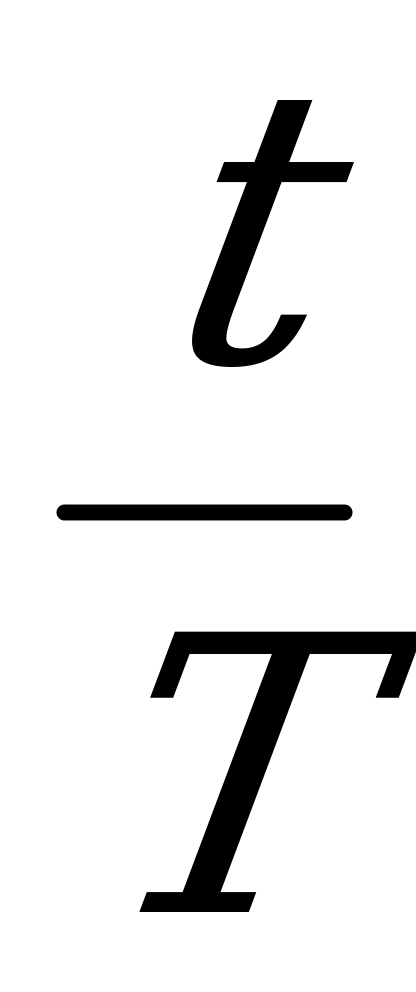 ,
,
где Т- период полураспада вещества, t - время, M - начальная масса вещества, m - масса через промежуток времени t.
Б) Балка - основной элемент строительной конструкции. В задаче о прочности балки используется функция h(x)=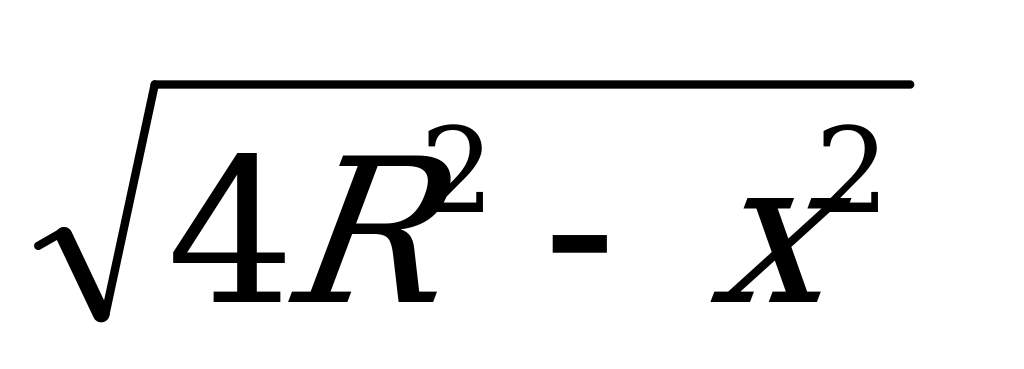 , где h- высота балки, имеющей ширину х, R - радиус бревна, из которого эту балку вытесали.
, где h- высота балки, имеющей ширину х, R - радиус бревна, из которого эту балку вытесали.
В) При расчете сложных оптических систем применяется функция t(х)=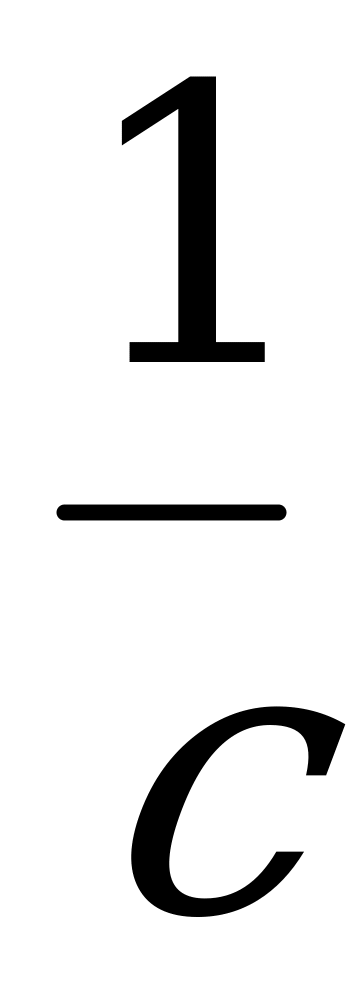 (
(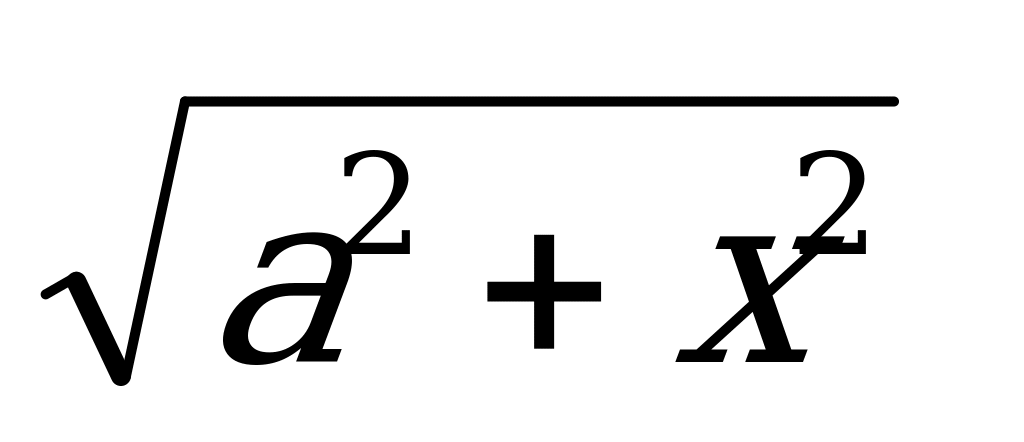 +
+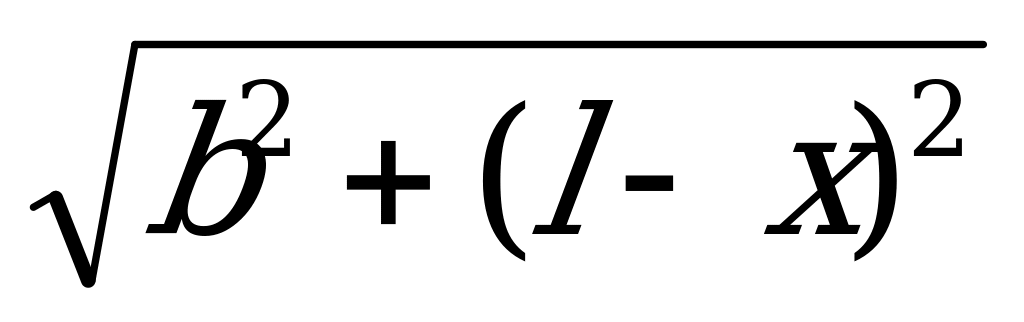 ), где t- время , за которое луч света проходит расстояние х от точки - начала движения до отражающей поверхности. Здесь с- скорость света, a, b, l- дополнительные измерения. Именно с помощью этой функции выведен закон физики о том, что угол падения равен углу отражения.
), где t- время , за которое луч света проходит расстояние х от точки - начала движения до отражающей поверхности. Здесь с- скорость света, a, b, l- дополнительные измерения. Именно с помощью этой функции выведен закон физики о том, что угол падения равен углу отражения.
Г) Многопудовый колокол, раскачиваясь под действием внешней силы, совершает так называемые вынужденные колебания. Они изменяются по закону: F(t)=B cos Ωt, где t- некоторый момент времени, Ω - частота возбуждающей силы, В - амплитуда.
Таким образом, мы видим многообразие в применении сложных функций в разных областях человеческой деятельности. И может быть благодаря им наш мир такой красивый и удивительный?...»
В это время один ученик у доски демонстрирует решение задачи из домашнего задания: Найти производную функции у=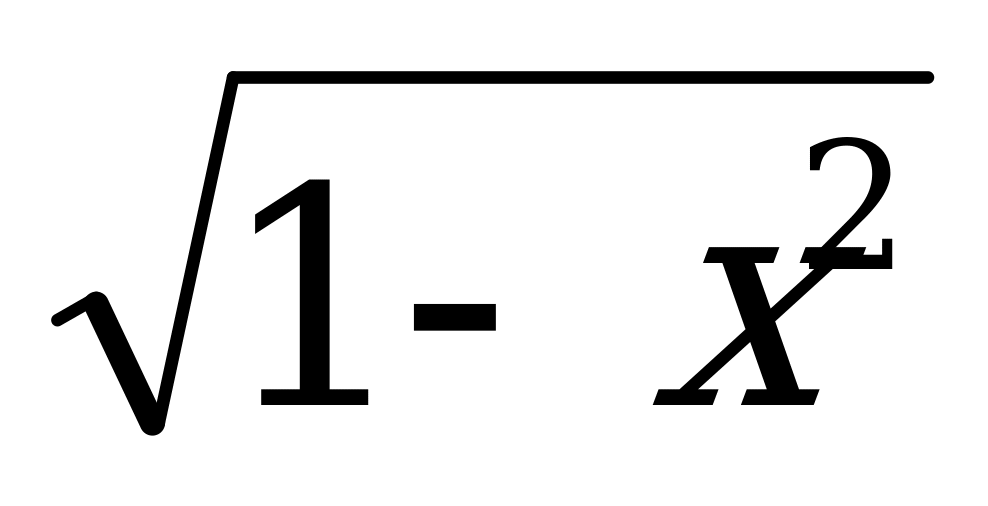 по определению .
по определению .
Когда мы подойдем к изучению приложений производной, нами будут рассматриваться практические задачи на оптимизацию (от латинского „оптимум”- наилучший), т.е. задачи на нахождение наибольшего и наименьшего значений. Сейчас мы услышали, насколько многогранно применение сложных функций. Поэтому, чтобы мы успешно умели принимать оптимальные решения, нужно научиться находить производную сложной функции.
V. Объяснение второй части нового материала.
Вернемся к вашему домашнему заданию и проверим , как вы нашли производную функции у= 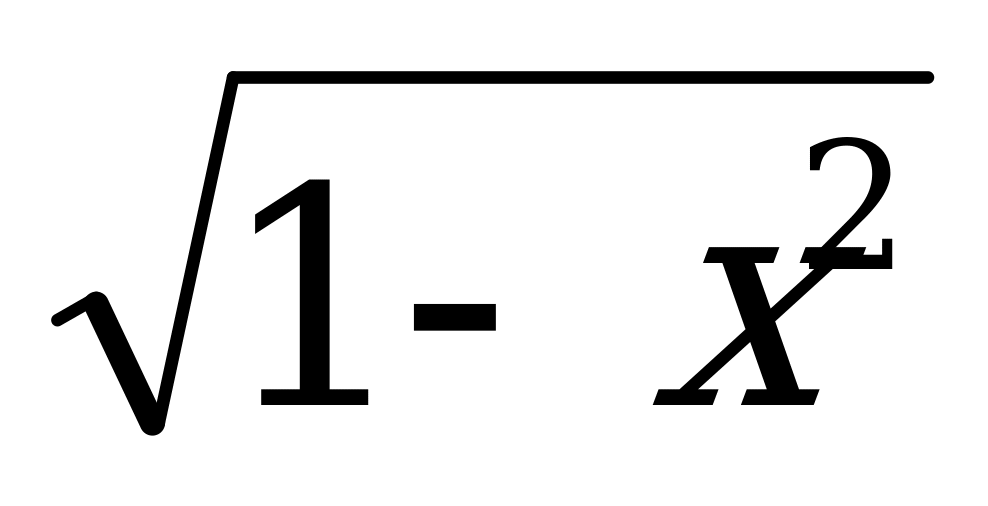 по определению. Ответ: -
по определению. Ответ: -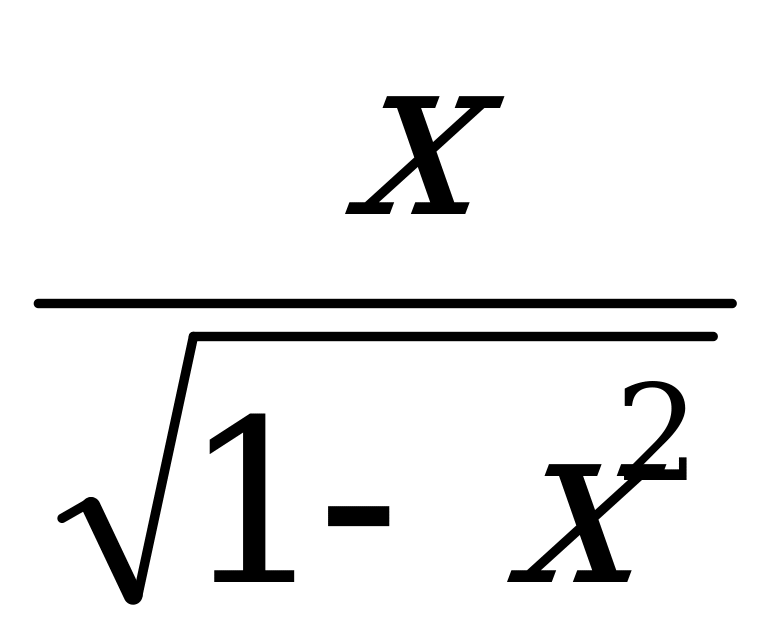
Но пользоваться всякий раз алгоритмом, как мы уже убеждались, неудобно, это кропотливая работа. А известные нам правила применимы только для елементарных функций. Поэтому необходимо еще одно правило - для нахождения производной сложной функции. Такое правило существует. Оно выведено на доске:
у=f(φ (х))
-
х, х+∆х.
-
∆у= f(φ (х+∆х)) - f(φ (х)) (*)
-
u=φ (х), φ (х+∆х)= φ (х)+ ∆φ (х), т.е. φ (х+∆х)= u+∆u.
-
(*)=f(u+∆u)- f(u), где ∆u ≠ 0, ∆u → 0, если ∆x→ 0.
-
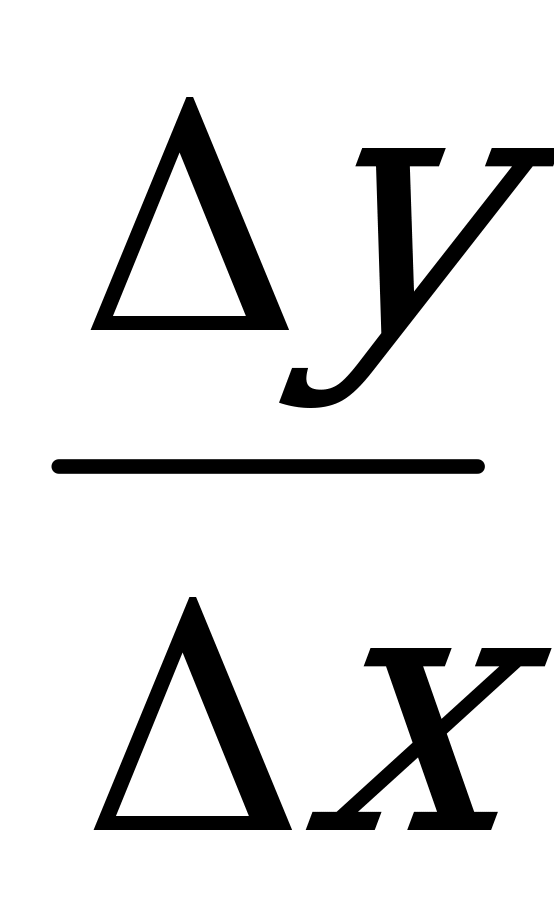 =
= 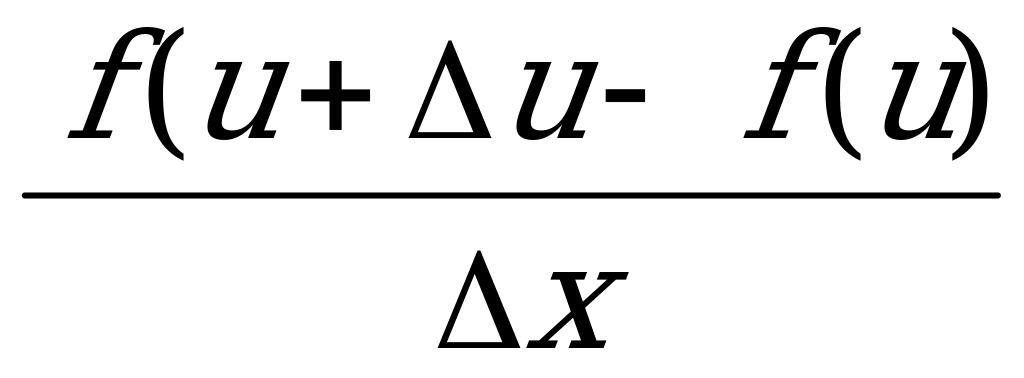 =
= 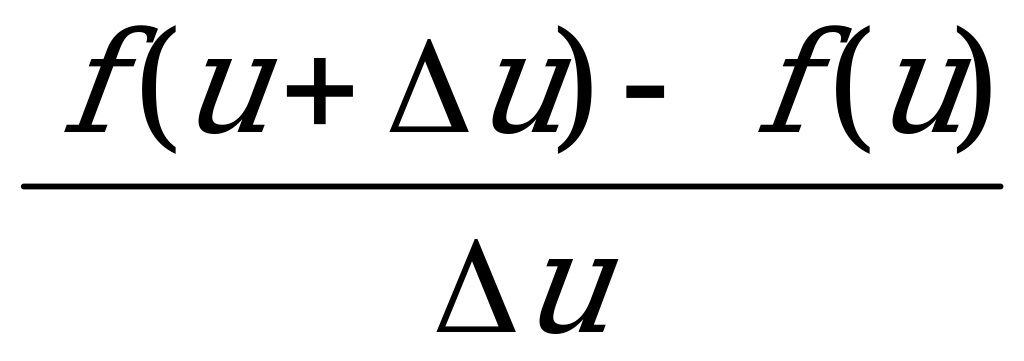 .
. 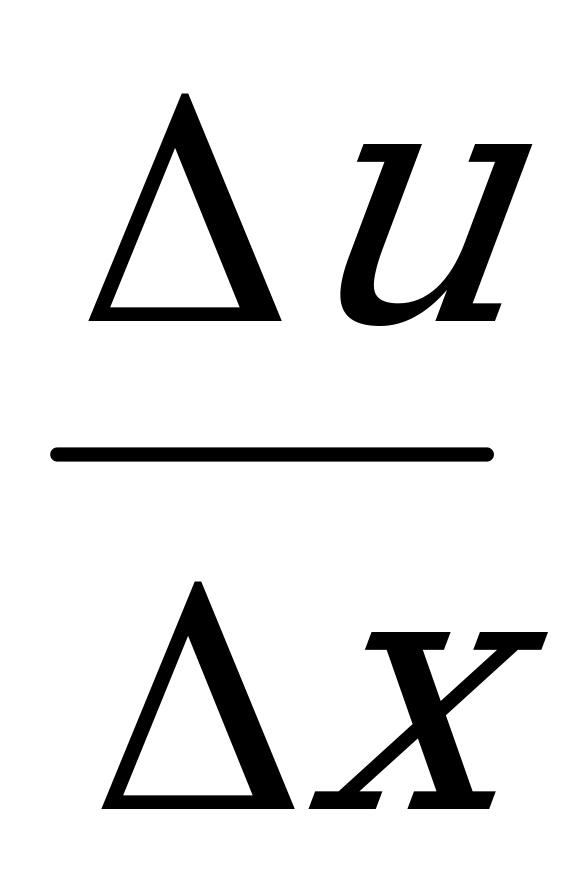
-
y/ (x)= 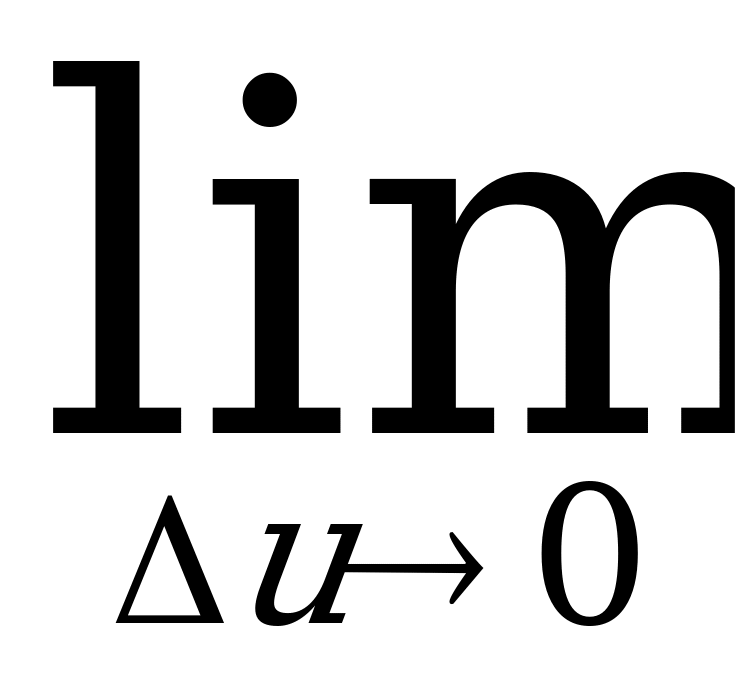
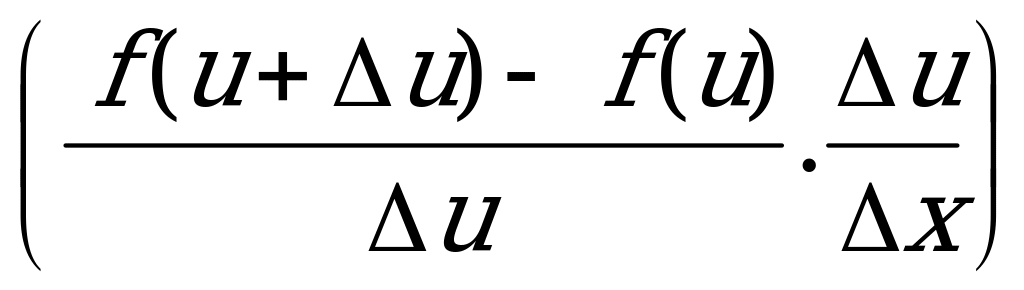 =
=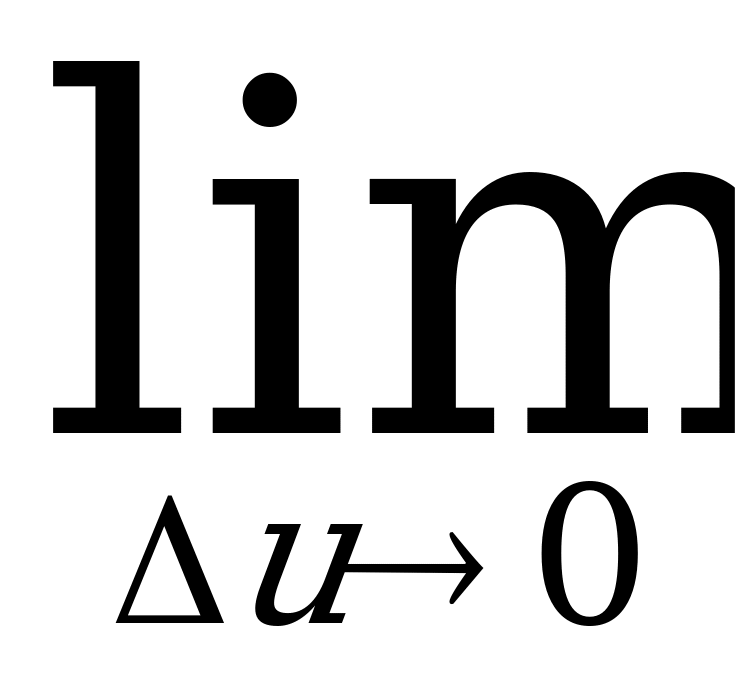
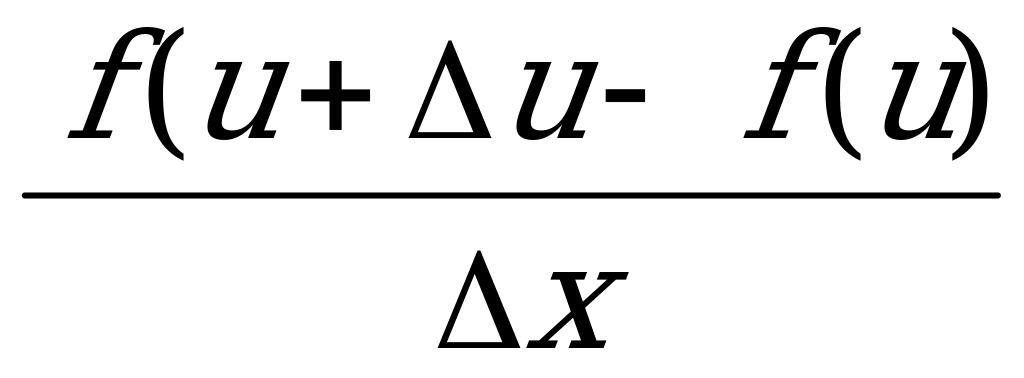 .
. 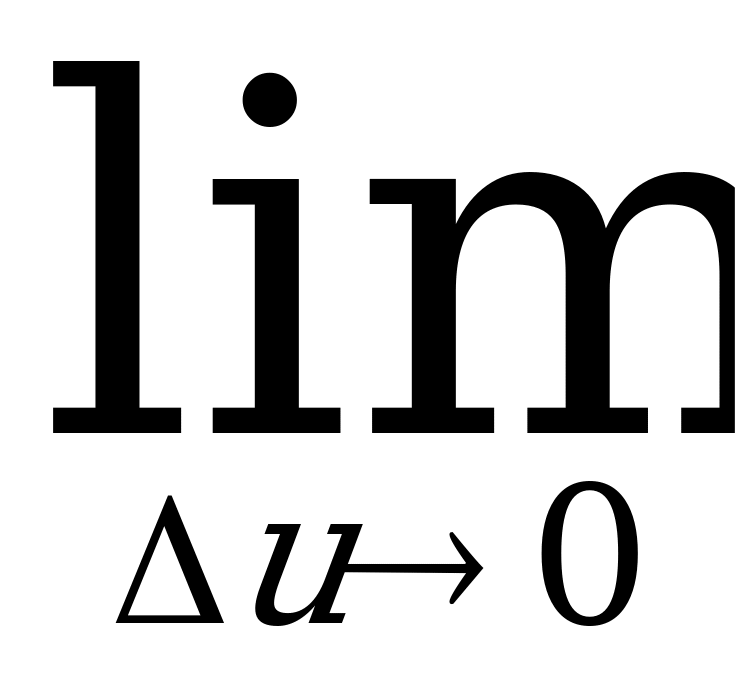
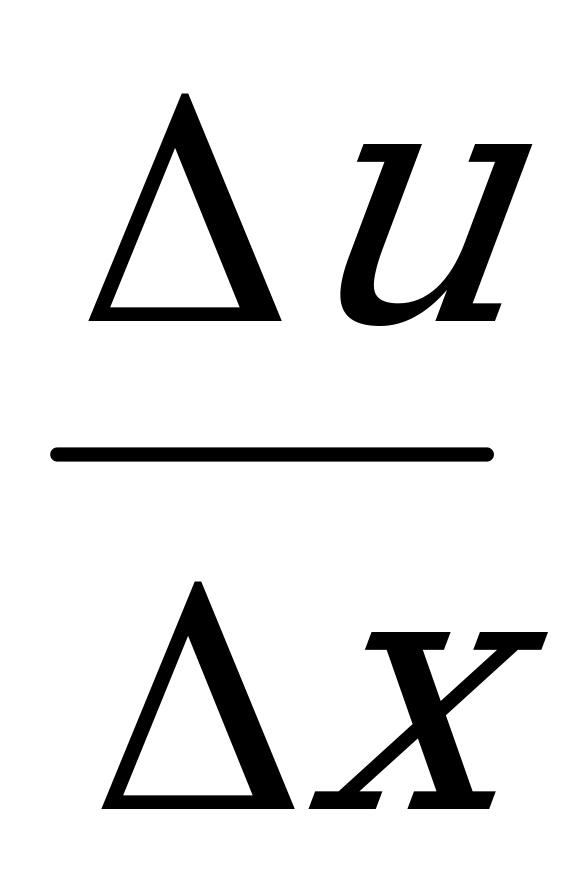 = f / (u) . u/
= f / (u) . u/
В учебнике вывод этой формулы есть. Но в том виде, в котором вы видите его на доске, он мне представляется более наглядным и доступным. Чтобы все выкладки здесь вам были понятны, вспомним некоторые теоретические вопросы.
VІ. Актуализация знаний. Закрепление материала.
Часть 1
Вопросы классу:
-
Дать определение возрастающей и убывающей функции.
-
Изобразить схематически график возрастающей функции, убывающей функции, отметить точку х0, показать приращение функции (∆х∆х 0).
-
Может ли приращение возрастающей или убывающей функции равняться нулю? (Нет). Почему? (Т.к. она монотонна, а не постоянна)
-
Сформулируйте определение производной.
-
Назовите алгоритм ее нахождения.
-
Как звучит лемма о приращении дифференцируемой функции?
Часть 2
Возвращаемся к выведению правила нахождения производной сложной функции.
Задание первому учащемуся: прокомментировать вывод формулы; заполнить пропуски
Задание второму учащемуся: дать словесную формулировку правилу.
Задание третьему учащемуся: Найти уравнение касательной к графику функции у=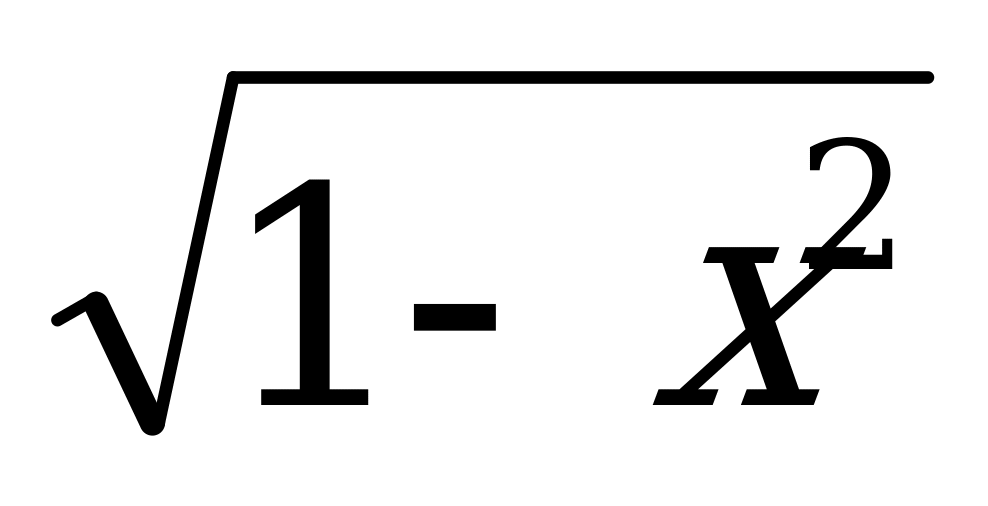 в точке х0 = 0. (Уравнение касательной имеет вид у=1)
в точке х0 = 0. (Уравнение касательной имеет вид у=1)
Комментарий учителя: Заметим, что графиком функции у=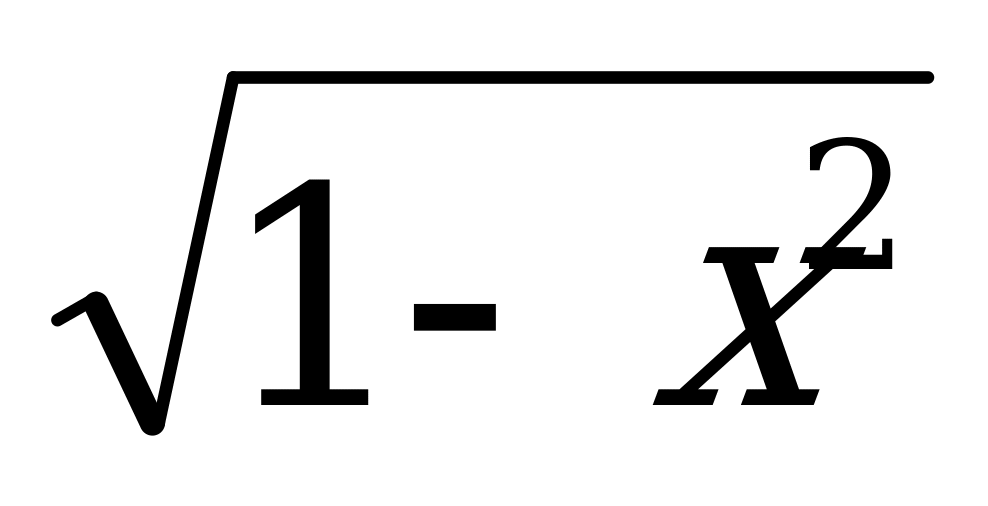 является полуокружность с центром в точке (0;0) и радиусом 1 ( этот материал мы изучали в 9 классе). Поэтому очевидно, что искомое уравнение касательной у=1.
является полуокружность с центром в точке (0;0) и радиусом 1 ( этот материал мы изучали в 9 классе). Поэтому очевидно, что искомое уравнение касательной у=1.
VІІ. Заключительная часть . Подведение итогов.
В этой связи, думаю, уместны будут слова известного немецкого математика Лейбница: «Кто хочет ограничиться настоящим без знания прошлого, тот никогда его не поймет».
Поэтому домашнее задание помимо нового материала будет включать повторение:
-
Выучить конспект урока.
-
Решить задачу: Покажите, что функция у=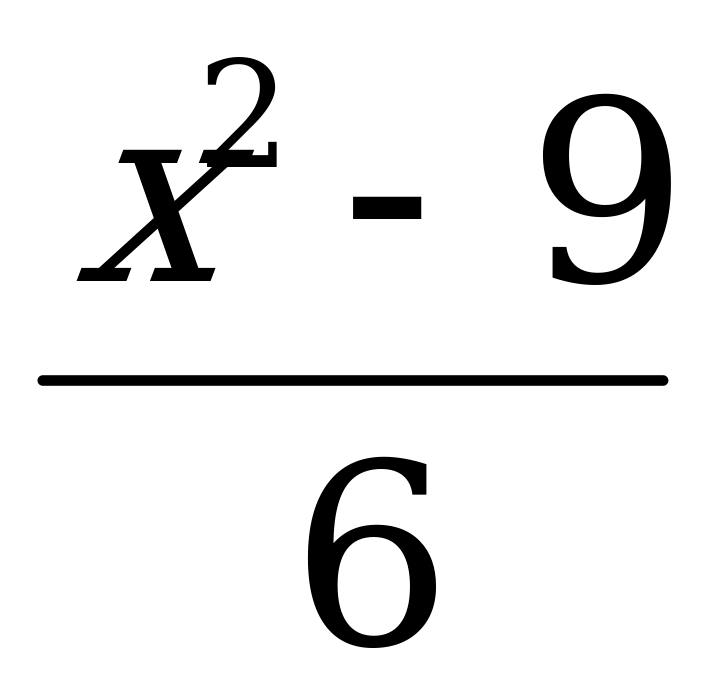 является решением дифференциального уравнения ху/ - y =
является решением дифференциального уравнения ху/ - y =  . Самостоятельно найти в литературе материал о дифуравнениях.
. Самостоятельно найти в литературе материал о дифуравнениях.
-
Повторить тему: «Тригонометрические уравнения».
На следующем уроке мы продолжим расширять свои знания по этой теме и формировать навыки по нахождению производных сложных функций.
Спасибо за урок!
11













 нашем примере (записываем на доске) f(u)=
нашем примере (записываем на доске) f(u)= 
 у = f ( g (х) ) - сложная функция
у = f ( g (х) ) - сложная функция а доске показан образец записи решения:
а доске показан образец записи решения: