Учитель математики Ксенофонтова Валентина Львовна
МБОУ Покровской ОШ
Даниловского района Ярославской области
Смысловое чтение при решении задач.
Задача №1 Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 часа больше, чем мотоциклист. Сколько км в час проезжал мотоциклист?
Первый этап-ознакомление с содержанием задачи
| Вопросы | Ответы |
| 1.О чем задача?
2.Что требуется узнать?
3.Как точнее выразить вопрос, что необходимо найти? 4. В вопросе есть единицы измерения км/час. Какая величина измеряется в этих единицах? Что требуется найти? 5. Что известно о движении мотоциклиста? 6.Какова скорость велосипедиста?
7.Известно ли расстояние, которое они проезжают? 8. Что известно о времени движения?
9. Сколько неизвестных в задаче? 10.Если два неизвестных, как их будете находить? 11. Что вы можете сказать о единицах измерения в задаче? 12.Как эту разницу в единицах можно использовать в составлении уравнений? 13. А какую разницу мы найдем во втором уравнении?
| О движении велосипедиста и мотоциклиста. Сколько км в час проезжал мотоциклист. Сколько км в час
Скорость мотоциклиста
Что он ехал быстрее велосипедиста? Скорость велосипедиста не дана, но он каждую минуту проезжал на 800м медленнее Они проезжают 30 км
Велосипедист затратил на 2 часа больше времени. Скорости велосипедиста и мотоциклиста. Надо будет составить два уравнения и объединить в систему. Есть м и км, часы и минуты, а должно быть км/час или м/мин. Надо м перевести в км, а минуту в часы и найти разницу равную 800м.
Разницу в 2 часа.
|
Наглядно представляем данные
По тексту задачи можно составить схему
Скорость велосипедиста
Х км/ час на 0,8 км меньше 30 км –весь путь
i______________________________________________________i
Скорость мотоциклиста Время на 2 часа быстрее
У км/час
По тексту задачи можно составить таблицу:
|
| Скорость | Время | расстояние |
| Велосипедист
мотоциклист | Х км/ч на 0,8 км меньше
У км/ч
| 1/60 ч
Больше на 2 часа | 30км
30 км |
Второй этап- от условия к заключению.
Составим систему уравнений
3 этап- решив систему уравнений найдем скорость мотоциклиста.
⌡1/60у-1/60х =0,8 /*60 у-х=48 у=48+х подставим во 2 ур.
⌠ 30/х=30/у +2 /* ух 30у=30х+2ху
30(48+х)=30х+2х(48+х)
1140+30х=30х+96х+2х2 /:2
Х2 +48х-720=0
Д=2304+2880=5184=722
Х1 =12
Х2 =-65 -не подходит у=48+12=60 (км/час)-х скорость мотоциклиста
Четвертый этап- проверка правильности решения
Подставим полученный результат путем подстановки в текст задачи.
Проверка результата к задаче 1
|
| Скорость | Время | расстояние |
| Велосипедист
Мотоциклист
| 12км/час
60 км/час | 30:12=15/6
30:60=3/6
| 30 км
30км
|
15/6-3/6= 12/6 = 2(часа)-велосипедист затратил времени на 2 часа больше, чем мотоциклист.
Ответ: 60км/час- скорость мотоциклиста.
Задача 2
Если давать корове по 10 кг сена в день, то заготовленного сена хватит на 120 дней. На сколько дней хватит этого сена, если давать в день на 2 кг больше?
Первый этап- ознакомление с материалом
| Вопросы | Ответы |
| 1.О чем задача?
1.Что требуется узнать в задаче?
2.Что известно о количестве сена?
3Можно ли найти, сколько было заготовлено сена?
4Если корова будет съедать в день больше на 2 кг, количество дней на, которые хватит сена, увеличатся или уменьшатся? | О времени расходования сена
На сколько дней хватит сена корове, если увеличить на 2 кг в день Что его хватит на 120 дней, если давать по 10кг. Можно
Надо сосчитать. |
Наглядно представляем данные
По тексту задачи можно составить схему:
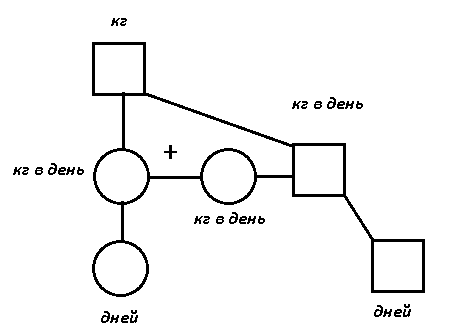
По тексту задачи можно составить таблицу:
|
| Кол-во сена в день | Кол-во дней | Кол-во заготовленного сена |
| Старый рацион | 10 кг | 120 | ? |
| Новый рацион | На 2 кг больше | ?(найти) |
|
Второй этап- поиск способа решения
Какой новый элемент можем найти с помощью составленной схемы и таблицы?
-Можно найти количество заготовленного сена.
3 этап- решить задачу.
10 х120= 1200 ( кг) сена было заготовлено
10+2=12(кг)
1200:12=100 (дней) – на которые хватит заготовленного сена, если корове давать 12 кг , а не 10.
Четвертый этап- проверка правильности решения
Подставим в условие задачи:
10х120=1200(кг)
12х100=1200(кг)
Ответ: 100 дней.
Задача 3.
Две бригады, работая вместе, должны отремонтировать заданный участок шоссейной дороги за 18 дней. В действительности же получилось так, что сначала работала только одна первая бригада, а заканчивала ремонт участка дороги вторая бригада, производительность труда которой более высокая, чем первой бригады. В результате ремонт заданного участка дороги продолжался 40 дней, причем первая бригада в свое рабочее время выполнила 2/3 всей работы. За сколько дней был бы
отремонтирован участок дороги каждой бригадой отдельно?
Первый этап- ознакомление с содержанием задачи.
| Вопросы | Ответы |
| 1.Кто действует? 2.Какую работу они выполняют?
3. Как они работали?
4.Работая « по-другому» сколько дней они работали? 5.За сколько времени они выполнили эту работу, работая вместе? 6.О чем спрашивается в задаче?
7.Сколько выполнялось за каждую единицу времени?
8.А во втором случае ?
9.Как это показать на схеме?
10.Как выразить объем работы?
11. Если работа неизвестна, как ее можно выразить?
| Две бригады Ремонтируют заданный участок дороги. Планировалось, что они должны работать вместе 18 дней, а получилось как всегда… Сначала работала одна бригада, а затем другая. За 40 дней.
За сколько дней отремонтировала этот участок дороги каждая бригада, если работала та или другая. В первом случае надо найти производительность, т. е разделить на 18 дней Во втором случае они работали вместе 40 дней. Первая сделала 2/3 всей работы, а второй осталось 1/3 Надо рассматривать 2 случая: 18 и 40 дней. Объем работы – это участок дороги, он неизвестен
Работу можно взять за 1. |
Наглядно представляем данные
По тексту задачи можно составить схему
Работали вместе-18 дней
1 бригада - х дней
2 бригада - у дней
1/18- производительность
i__i__i__i__i__i__i__i__i__i__i__i__i__i__i__i__i__i__i
2/3
Работали отдельно -40 дней.
1 бригада выполнила -2/3 всей работы
3 этап – Составление таблицы
|
| Кол-во дней |
| производительность | работа |
|
1 бригада 1 бригада
| Работали Х дней У дней | Вместе 18дней 18 дней |
1/18 х 1/18 у |
1 1 |
|
1 бригада 2 бригада | Работали Х дней ? У дней ?
| Отдельно
40 дней
|
2/3х 1/3 у |
2/3 всей р. 1/3 всей р. |
Решение.
Пусть вся работа может быть выполнена первой бригадой за х дней,
а второй за у дней.
2.Принимаем всю работу за 1, имеем:
1\х – производительность первой бригады,
1\у – производительность второй бригады,
1\х *18 –часть работы, которую могла бы выполнять первая бригада за 18
дней.
1\у *18 –часть работы, которую могла бы выполнять вторая бригада за 18
дней.
Составим уравнение
Так как обе бригады, работая совместно, могли выполнять всю работу за 18 дней, то на основании этого имеем
1\х*18 + 1\у*18 =1 (1)
Далее из условия задачи известно, что первая бригада выполнила 2\3 всей работы, следовательно, она затратила на это 2\3 *х дней, а вторая бригада выполнила 1\3 всей работы, следовательно, она затратила на это 1\3 *у дней
Так как всего было затрачено 40 дней, то можно составить второе уравнение:
2\3 *х + 1\3 *у =40 (2)
Уравнения (1) и (2) объединим в систему
1\х *18 +1\у *18 = 1 /*ху 18у +18х =ху
2\3 х + 1\3у =40 /*3 2х +у =120 у=120-2х
Подставляя в первое уравнение, получим
Х2 +69х -1089 =0 х1 = 45 , х2 =24
У1 =72 , у2 =30
6. Так как производительность второй бригады была выше, чем первой, то условию задачи удовлетворяют х=45 и у=30.
Четвертый этап- проверка правильности решения
Пусть известно, что первая бригада может выполнить всю работу за 45 дней, а вторая бригада –за 30 дней, тогда первая бригада за 1 день выполнит 1\45 часть всей работы, а вторая бригада = 1\30 всей работы, и , следовательно, вместе за 1 день они выполнят
1\45 +1\30 =5\90 =1\18 всей работы. Значит, им понадобится на выполнение всей работы 18 дней, что соответствует условию задачи.
Рассуждая аналогично получим, что первая бригада выполнит 2\3 всей работы за 2\3 * 45 =30 дней, а вторая бригада выполнит 1\3 всей работы за 1\3 * 30 =10 дней , т. е всего будет затрачено
30 + 10 =40 дней, что соответствует условию.
Ответ: 45 дней, 30 дней.
Задача 4. Лодка проплыла по течению реки расстояние между двумя пристанями за 6 часов. А обратный путь она совершила за 8 часов. За сколько времени пройдет расстояние между пристанями плот, пущенный по течению реки?
Первый этап – Ознакомление с содержанием задачи
| Вопросы | Ответы |
| 1.Сколько действующих объектов в задаче? 2.Лодка имеет собственную скорость? 3. Скорость плота, реки? Что-нибудь известно? 4. Сколько неизвестных в задаче? 5. Что необходимо найти в задаче? 6. Выходит скорости и путь находить не надо? 7 В чем вопрос?
8.Но, что-то известно в задаче?
9. О чем говорит это время?
10. Почему она шла быстрее? 11.Какие данные негласно присутствуют в задаче? 11.Что необходимо знать, чтобы ответить на вопрос задачи? | Два объекта: лодка и плот
Собственная скорость лодки неизвестна. Нет.
Неизвестны все скорости и путь. За какое время пройдет плот по течению. Выходит не надо.
Как решить задачу со всеми неизвестными? Время лодки по течению 6 часов, а против течения 8 часов. Лодка по течению плыла быстрее. Ей помогало течение реки Наверное, путь и течение реки
Надо обозначить все неизвестные и пробовать решать. |
Наглядно представляем данные.
По тексту задачи можно составить схему
Лодка 6 часов
-------»
А i_________________________________i В
-------» «----------
Плот Лодка
8 часов
Второй этап- поиск способа решения
Будем считать , что скорость лодки , течения реки и путь нам известны. Это значит, что мы их можем ввести в условие задачи.
Нужно найти время, за которое плот проплывает расстояние между пристанями А и В. Для того чтобы найти это время, надо знать расстояние АВ и скорость течения реки. Оба они неизвестны, поэтому обозначим расстояние АВ буквой S (км), а скорость течения реки примем за а (км\час)
Собственную скорость лодки обозначим через v (км\час)
По тексту задачи можно составить таблицу.
|
| .Скорость | Время | Расстояние |
| Собственная скорость лодки | v (км\ч) |
| |
| По течению | v+а (км\ч) | 6 ч | 6*(v+а) = S |
| Против течения | V - а(км\ч) | 8 ч | 8*(v-а) = S |
| Течение реки | а (км\ч) |
|
|
| Плот | а (км\ч) | X ч | а*х=S |
3 этап- Оформление решения
6*(v+а) =S (1)
8*(v-а) =S (2)
а*х =S (3)
Уравнения (1), (2), (3) образуют систему уравнений относительно неизвестных s, а, v и х . Так как требуется найти лишь х, то от остальные неизвестные постараемся исключить
Для этого из уравнения (1) и (2) найдем
V+а= S\6
v- а =S\8 Вычитая из первого уравнения второе, получим
2а= S\6 – S\8 а=S\48. Подставим найденное выражение для а в уравнение (3)
S\48*х = S
Так как, очевидно, S не равно нулю, то можно обе части полученного уравнения разделить на S. Тогда найдем: Х=48
Четвертый этап - проверка правильности решения
Проверка результата в задаче 4.
Итак, мы нашли, Что плот проплывает между пристанями за 48 часов. Следовательно, его скорость равна скорости течения реки, равна S\48(км\ч)
Скорость лодки по течению реки S\6 (км\ч), а против течения S\8 (км\ч)
Сравним собственную скорость лодки найденную двумя способами.
S\6 –S\48 = S\8 +S\48
7S\48 = 7S\48
Значит, задача решена правильно.
Ответ: плот проплывает расстояние между пристанями за 48 часов.
Эту задачу можно было решить короче, не составляя систему уравнений.
Зная , что лодка проплыла расстояние АВ по течению реки 6ч, а против течения 8 часов, найдем, что в 1ч лодка, идя по течению, проходит 1\6 часть , а против течения 1\8 . Тогда разность между ними есть удвоенная часть расстояния АВ, проплываемая плотом за 1ч.
1\6 -1\8 = 1\24 Значит плот за 1 час проплывает 1\48 часть расстояния АВ, следовательно, все расстояние АВ он проплывает за 48 часов.
Задача 5.Два человека выполняют одинаковое задание. У кого скорость больше : кто завершает эту работу за 6 часов или кто завершает за 8 часов?
| Вопросы | Ответы |
Сколько участников действует? Начинают и кончают они вместе или нет? Что надо найти в задаче? А что требуется узнать? . 5.Что известно про объем . работы?
| Два человека Это не важно. Главное объем работы один. Ничего. Сравнить ,кто выполнит работу быстрее.
Объем неизвестен. Надо взять ее за 1 |
Наглядно представляем данные
По тексту задачи можно составить схему:
1 работник
i____i_____i______i_____i_______i_____i
2 работник
I___i____i____i____i____i____i_____i_____i
|
| Скорость | . Время | Работа |
| 1.работник | 1\6 | 6 ч | 1 |
| 2 работник | 1\8 | 8ч | 1 |
Сравним 1\6 больше 1\8 т.к. 4\24 больше 3\24
Ответ: у работника, который выполняет работу за 6 часов скорость больше, чем у работника, который выполняет работу за 8 часов.



























