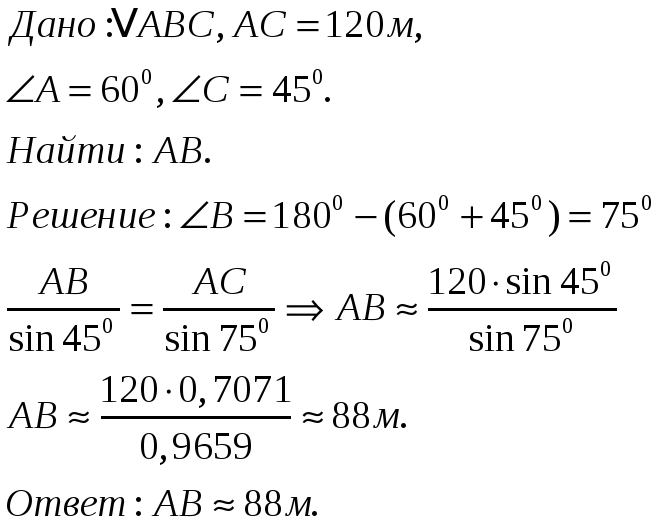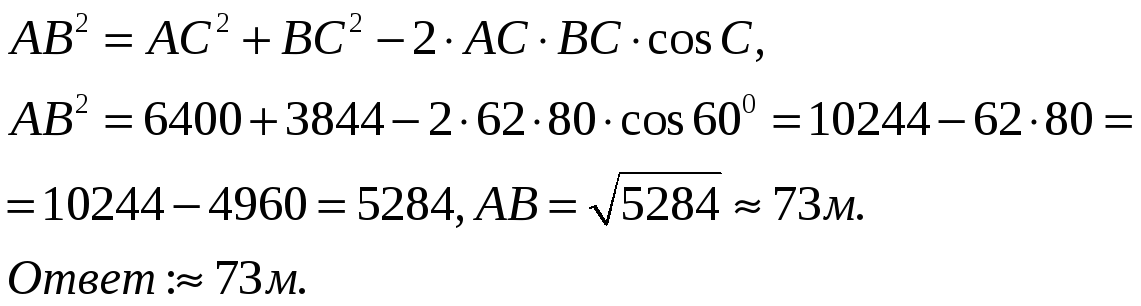Соотношения между сторонами и углами треугольника

Приложение 1

ИСТОРИЯ ТРИГОНОМЕТРИИ

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon - треугольник, а metrew- измеряю).

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение  тригонометрии связано с землемерением, астрономией и строительным делом.

Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский  астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия.  Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги.

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ (рис. 1) он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками  в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в  веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa =  sin( 90° - a)).

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов.  Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г.  Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греческого gwnia - угол,  metrew- измеряю). Термин гониометрия в последнее время практически не употребляется.

Обобщающий урок математики в 9 классе по теме: «Соотношения между сторонами и углами треугольника».

Карабетова Марет Ереджибовна учитель математики.

Тема урока: Обобщающий урок в 9 классе по теме: «Соотношения между сторонами и углами треугольника».

Цель урока:

1. Повторить определения синуса, косинуса, тангенса, основные тригонометрические тождества, формулы приведения;

2. повторить теорему о площади треугольника, теорему синуса, теорему косинуса;

3. решить треугольник, по каким - нибудь трем данным элементам, определяющим треугольник;

4. закрепить и проверить знание основных формул раздела;

5. умение применять их при решении задач;

6. развивать логическое мышление, умение делать выводы, обобщать;

7. развивать навыки самостоятельной работы;

8. воспитывать аккуратность, наблюдательность, самостоятельность.

Форма урока: урок – беседа.

Оборудование и материалы для урока: компьютер, проектор, экран.

Ход урока:

Учитель: - Ребята! Сегодня у нас обобщающий урок по теме: «Соотношения между сторонами и углами треугольника». Исходя из формулировки темы, какие цели вы должны поставить перед собой на сегодняшний урок?

Ученик: - Необходимо повторить весь теоретический материал и применить его при решении задач. (слайд 2), для этого поставим перед собой следующие цели:

1. Знать определения синуса, косинуса, тангенса, тангенса.

2. Знать теорему о площади треугольника, теорему синуса, теорему косинуса.

3. Уметь решить треугольник, по каким - нибудь трем данным элементам, определяющим треугольник.

4. Уметь применять основные формулы раздела при решении задач.

Учитель: - Для достижения этой цели будем идти по следующему маршруту (слайд 3):

Этапы урока:

1. Разминка.

2. Актуализация имеющихся знаний

3. Решение задач. Практическая работа.

4. Историческая справка

5. Где можно применить полученные знания на практике в жизни.

6. Домашнее задание.

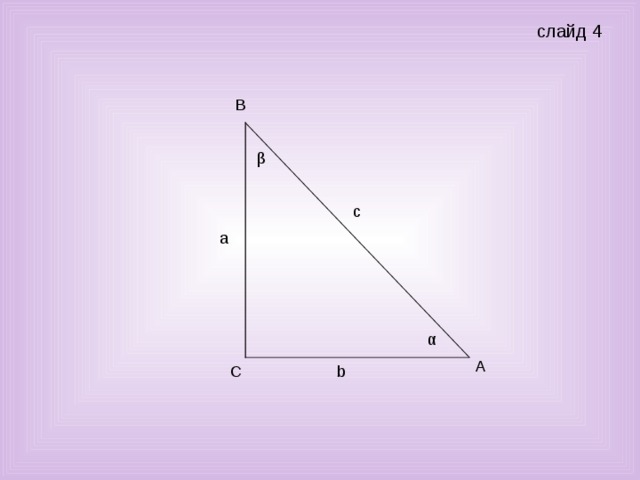
Учитель (показывает на слайде 3): - В прямоугольном треугольнике ∆АВС, примем ‹С= 90º, АВ=с, АС=b, ВС=a. ‹А= α, ‹В=β. Как называются стороны прямоугольного треугольника, и что означают эти названия?

Ученик: Катет – одна из двух сторон прямоугольного треугольника, образующих прямой угол. Название «катет» происходит от греческого слова katetos – перпендикуляр, опущенный, отвесный. Название «катет» встречается также в архитектуре и означает отвес через середину задка ионической капители.

Ученик: Гипотенуза – самая длинная сторона прямоугольного треугольника, противоположенная прямому углу. Название «гипотенуза» происходит от греческого слова, в переводе означает натянутая. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.

Ученик: С катетами и гипотенузой связаны тригонометрические функции острого угла α. (показывает на слайде 4)

sinα = a/с;

cosα = b/с;

tgα = а/b

сtgα = b/а

secα = c/b

cosecα = c/a

• синус α — отношение катета, противолежащего углу α, к гипотенузе.

• косинус α — отношение катета, прилежащего углу α, к гипотенузе.

• тангенс  α — отношение катета, противолежащего углу α, к катету прилежащему углу α.

• котангенс α — отношение катета, прилежащего углу α, к катету противолежащему углу α.

• секанс α — отношение гипотенузы к катету прилежащему углу α.

• косеканс α — отношение гипотенузы к катету противолежащему углу α.

Учитель: Как найти длину катета.

Ученик: Длина катета может быть найдена с помощью теоремы Пифагора, которая утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов:

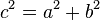
Длина катета равна произведению длины гипотенузы и косинуса прилежащего угла:

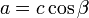
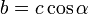
Длина катета равна произведению длины гипотенузы и синуса противолежащего угла:

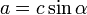
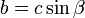
Длина катета равна произведению длины другого катета и тангенса противолежащего угла, относительно искомого катета:

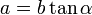
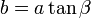
Длина катета равна произведению длины другого катета и котангенса прилежащего угла, относительно искомого катета. Длина катета равна среднему геометрическому длины гипотенузы и длины проекции этого катета на гипотенузу:

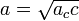
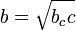
Квадрат высоты, выходящей из прямого угла, равен произведению проекций катетов на гипотенузу:

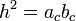
Где

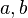 — катеты

 — гипотенуза

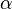 — угол, противолежащий a

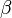 — угол, противолежащий b

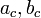 — проекции катетов a и b на гипотенузу.

С катетами совпадают две из трёх высоты прямоугольного треугольника.

По катету и гипотенузе или по двум катетам можно судить о равенстве двух прямоугольных треугольников.

Вращая прямоугольный треугольник вокруг катета можно получить прямой круговой конус. (слайд 5)

Учитель: Решим теперь задачи, в каждом случае объяснить как найти х и дать

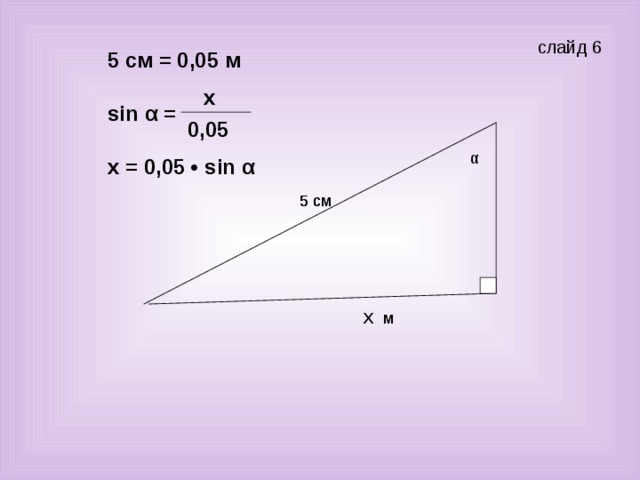
определение геометрическому понятию. Найти х. (слайд 6)

Ученик: Так как х – противоположенный катет углу α, то воспользуемся определением синусов. Синусом острого угла называется отношение противолежащего катета к гипотенузе, т.е.

sinα= х/0,05, так как х нужно найти в метрах, получаем х = 0,05•sinα.

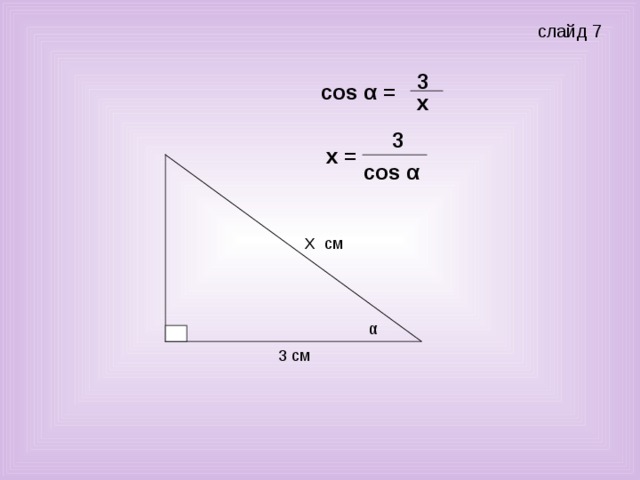
Учитель: Хорошо. Следующая задача. Найти х. (слайд 7)

Ученик: Так как по условию задачи знаем прилежащий катет и нужно найти гипотенузу, то из определения косинуса, можем записать cosα = 3/х. Т.е.

х = 3/ cosα

(так как косинусом острого угла называют отношение прилежащего катета к гипотенузе ).

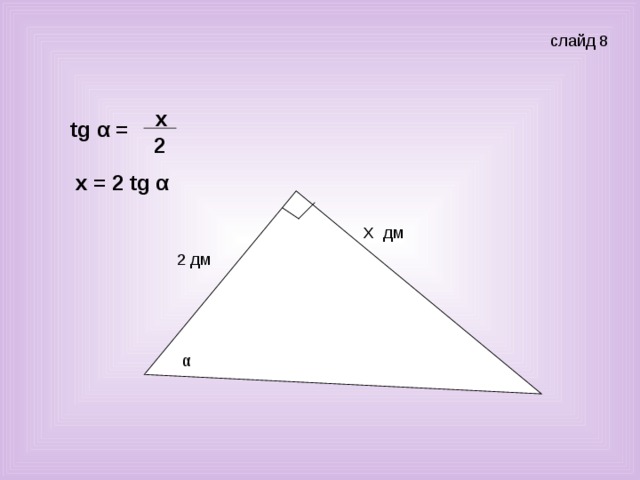
Учитель: Хорошо. Решите задачу. Найти х. (слайд 8)

Ученик: Зная угол и прилежащий катет, можно найти противолежащий катет, исходя из определения тангенса, так как тангенсом острого угла называется отношение противолежащего катета к прилежащему, т.е.

tgα = х/2, отсюда х = 2 tgα .

Учитель: И так мы дали определения и записали формулы. А для чего все – таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна 180º. Знаем соотношения между сторонами прямоугольного треугольника. Это теорема Пифагора:

а² + b²=c²

Получается, что зная два угла в треугольнике можно найти третий угол. Зная две стороны в прямоугольном треугольнике можно найти третью. Значит, для углов – свое соотношение, для сторон – свое. А что делать если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника. Синус, косинус и тангенс – их еще называют тригонометрическими функциями угла, дают соотношения между сторонами и углами треугольника. Зная угол можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы, тангенсы углов треугольника и одну из его сторон можно найти остальные элементы.

Как же развивался раздел математики, где изучаются эти понятия.

Ученик: Этот раздел математики называется тригонометрией. Тригонометрия прошла интересный жизненный путь. ( Доклад ученика. Приложение 1)

Учитель: Таким образом, тригонометрия возникла как наука о решении треугольников. Способы решения треугольников впервые были письменно изложены греческим астрономом Гиппархом в середине II века до н.э. Наивысшими достижениями греческая тригонометрия обязана астроному Птолемею (II век до н.э), создателю

геоцентрической системы мира, господствовавшей до Коперника.

Решить треугольник означает определить стороны, углы и другие элементы треугольника, если даны некоторые из них. Какие теоремы, свойства и определения используем при этом? Ответы мы получим, решая задачи. В каждой задаче объясните какая теорема использована.

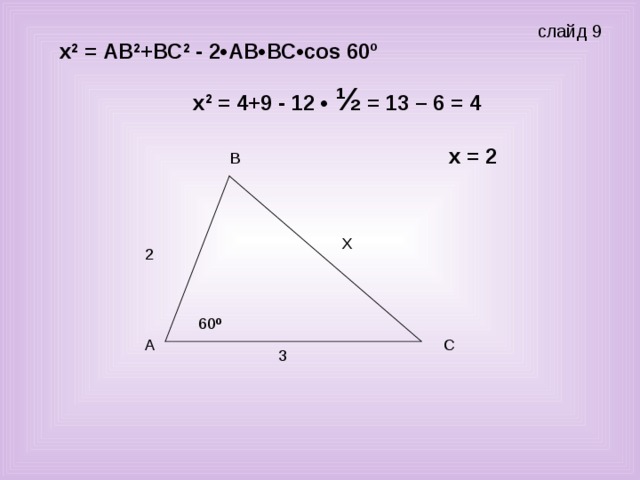
Задача № 1. (слайд 9) Найти Х.

Ученик: - Так как нам известны две стороны и угол между ними , то чтобы найти сторону х, достаточно воспользоваться теоремой косинусов: «квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними». Тогда

х² = 2²+3² - 2•2•3 соs 60º = 4+9 - 12 • ½ = 13 – 6 = 4. т.к соs 60º=1/2

Ответ : 4.

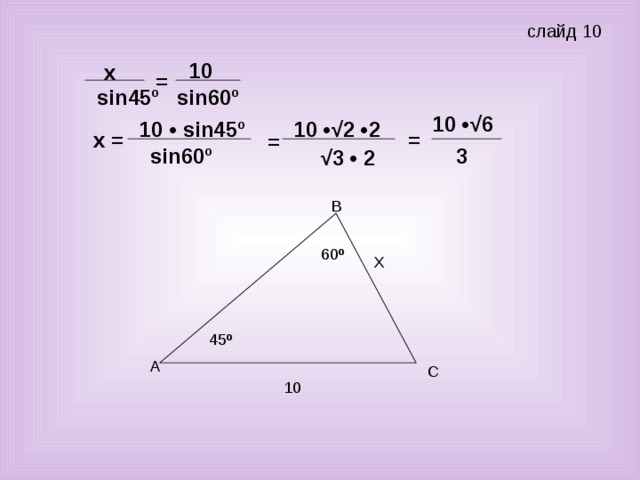
Учитель: Задача № 2. (слайд 10) Найти Х.

Ученик: - Так как нам известны два угла и сторона треугольника, то х можно найти по теореме синусов: «Стороны треугольника пропорциональны синусам противолежащих углов». Имеем

х : sin45º = 10 : sin60º; х = 10•sin45º : sin60º = ^{10 •√2 : 2} = ^{5 •√2 • 2} = ^{10 •√6}

^{√3 : 2 √3 3}

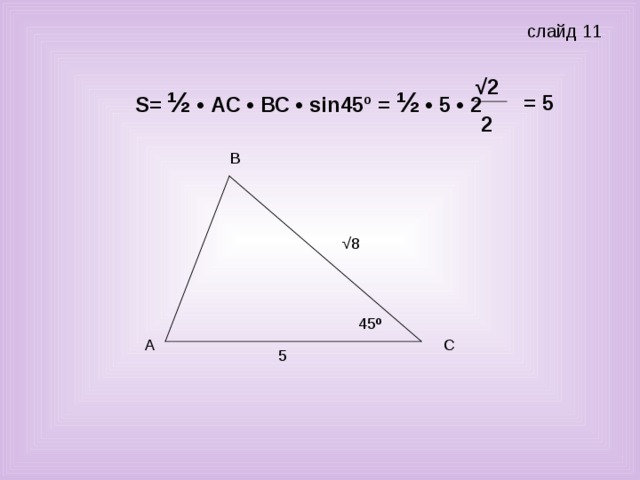
Учитель: Задача № 3. (слайд 11) Найти площадь треугольника.

Ученик: - Зная две стороны и угол между ними, площадь треугольника можно по теореме о площади треугольника: «Площадь треугольника равна половине произведения двух его сторон на синус угла между ними». Получаем

S= ½ • 5 • √8 • sin45º = ½ • 5 • 2√2 • √2 : 2 = ½ • 5 • 2 = 5

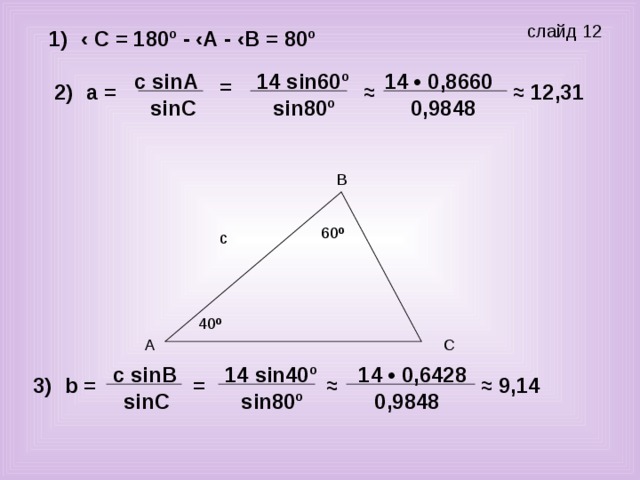
Учитель: Повторили основные теоремы данного вопроса. Решим теперь треугольник. № 1025 (а) (слайд 12).

Ученик (объясняет):

Дано: Решение:

‹А = 60º 1) По теореме о сумме углов треугольников находим ‹С:

‹В = 40º ‹ С = 180º - ‹А - ‹В = 180º - 60º - 40º = 80º

с = 14 2) По теореме синусов находим a и b:

Найти а = с sinА/ sinС = 14 sin60º / sin80º ≈ 14 • 0,8660 / 0,9848 ≈ 12,31

‹С, a, b. 3) b = с sinВ/ sinС = 14 sin40º / sin80º ≈ 14 • 0,6428/0,9848 ≈ 9,14

Значения синусов для данных углов определяем по таблицам.

Ответ: ‹С= 80º, a ≈ 12,31, b ≈ 9,14.

Ученик (объясняет) № 1025 (в) (слайд 13):

Дано: Решение:

‹А = 80º 1) По теореме синусов находим с:

а = 16 sinВ/b = sinА/а;

b = 10 sinВ = b•sinА/а = 10•sin80º/16 ≈ 10•0,9848/16 ≈ 0,6155

2) Получаем два значения для ‹В

‹В - ? ‹В₁ = 37º 59 

‹С - ? ‹В₂ = 142º1 

с - ? так как ‹А + ‹В₂ › 180º, то ‹В = ‹В₁ = 37º 59 

3) ‹С = 180º - ‹А - ‹В = 180º - 80º - 37º 59  = 62º1 

4) с = а sinС/sinА = 16 sin62º1 /sin80º ≈ 16•0,8830/0,9848 ≈ 14,35

Ответ: ‹В= 37º 59 , ‹С = 62º1 , с ≈ 14,35.

Учитель: Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

Ученик: В треугольнике АВС угол С равен 90º, sinА = 0,1. Найдите cosВ.

Поскольку А + В = 90º, sinА = cosВ = 0,1.

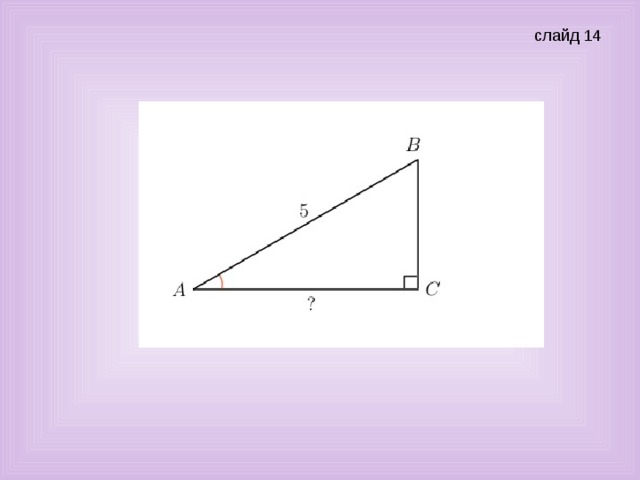
Учитель: В треугольнике АВС угол С равен 90º, АВ = 5, sinА = 7/25 (слайд 14). Найдите АС.

Ученик: Решение: 1) sinА = ВС/АВ, ВС = АВ• sinА = 5• 7/25 = 7/5.

2) Найдем АС по теореме Пифагора.

Задача решена.

Учитель: Часто в задачах встречаются треугольники с углами 90º, 30º и 60º или с углами 90º, 45º и 45º . Основные соотношения для них запоминайте наизусть! (слайд 15).

Для треугольника с углами 90º, 30º и 60º  катет, лежащий напротив угла в 30º равен половине гипотенузы.

Треугольник с углами 90º, 45º и 45º — равнобедренный. В нем гипотенуза в √2 раз больше катета.

Реши сам! (Ученики решают самостоятельно, решение проверяем (слайд 16)).

Задача : В треугольнике даны две стороны а = 6, b = 8 и противолежащий стороне а, угол α = 30º. Найти остальные два угла и третью сторону.

Дано: Решение:

АВС 1) По теореме синусов находим значение sinВ:

ВС = 6 sinβ/b = sinα/а;

АС = 8 sinβ = b•sinα/а = 8 sin30º/6 ≈ 0,667.

‹А = α 2) Этому значению синуса соответствует два угла:

АВ - ? ‹β₁ ≈ 42º и ‹β₂ ≈138º

‹В - ? 3) Пусть ‹β₁ ≈ 42º , тогда

‹С - ? ‹γ₁ = 180º - α – β ≈108º, и по теореме синусов третья сторона

с₁ = а •sin γ₁ / sinα = 6 •sin108º / sin30º ≈ 6 • 0,951 / 0,500 ≈ 11,4

1. Аналогично по углу ‹β₂ ≈138º находим

‹γ₂ = 180º - α – β ≈12º

с₂ = а •sin γ₂ / sinα = 6 •sin12º / sin30º ≈ 6 • 0,2079 / 0,500 ≈ 2,49

Учитель: Эта задача в отличие от предыдущих имеет два решения. При других численных данных, например при α ≥ 90º задача может иметь лишь одно решение или вовсе не иметь решений.

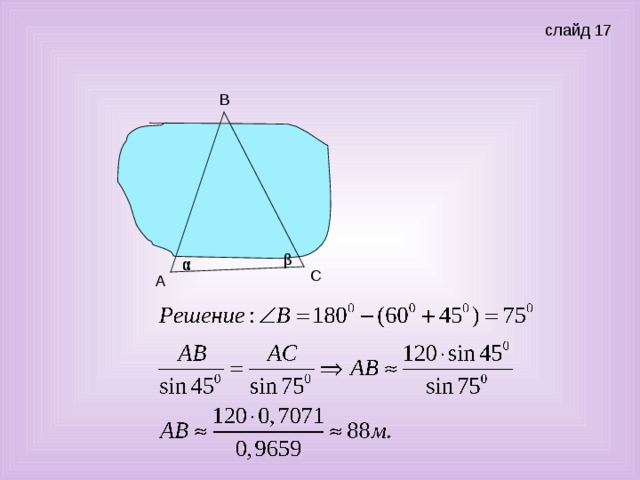
Решим следующую задачу. Найти ширину озера АВ, если АС=120м, 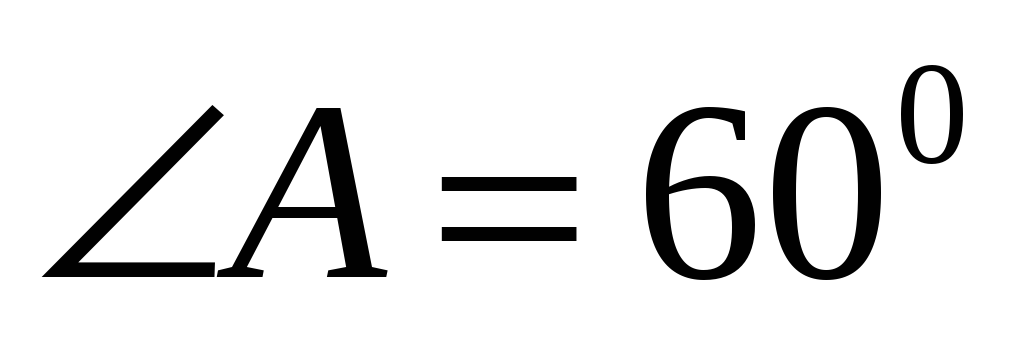,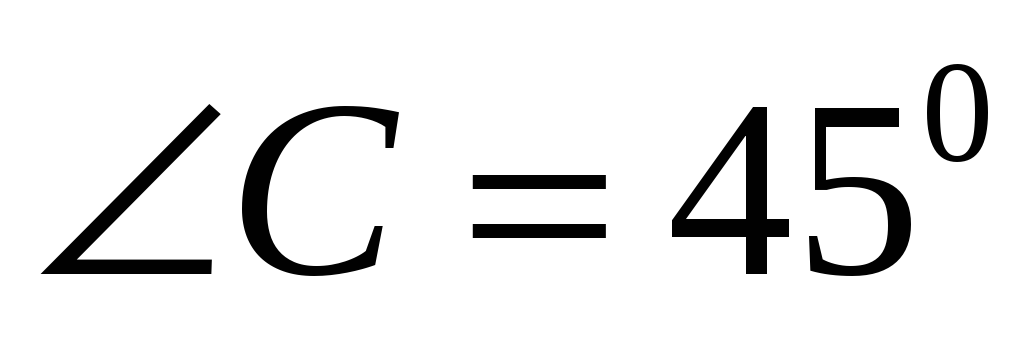. (слайд 17)

Ученик: Решение:

Дано АВС, АС = 120 м,

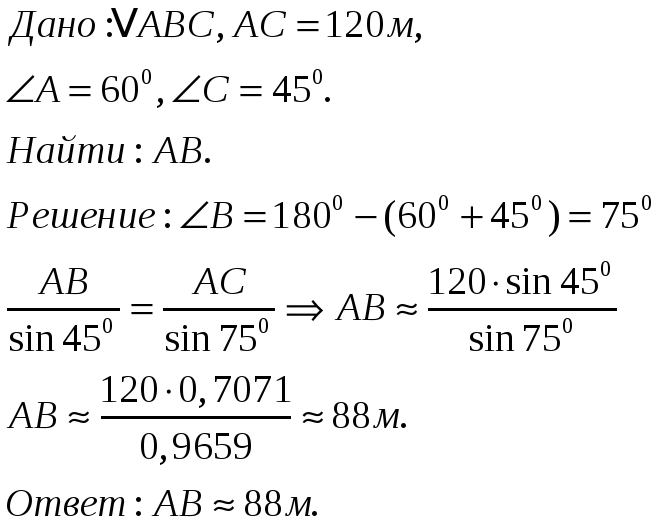
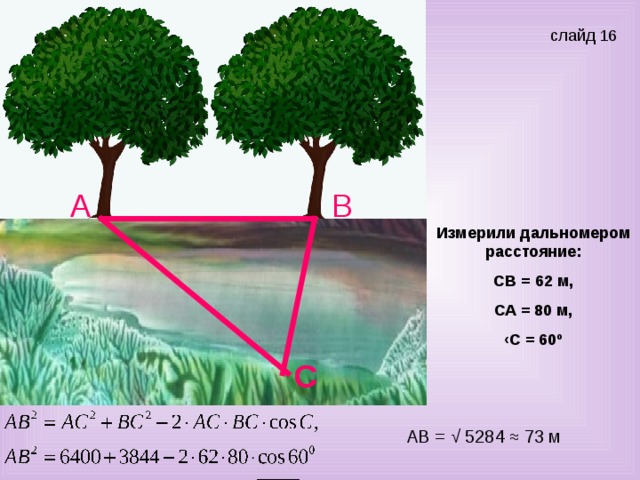
Учитель: Измерили дальномером расстояние СВ=62м, СА=80м. Угол между ними 60⁰. Найдите расстояние между двумя деревьями А и В. (слайд 18)

Ученик: Решение:

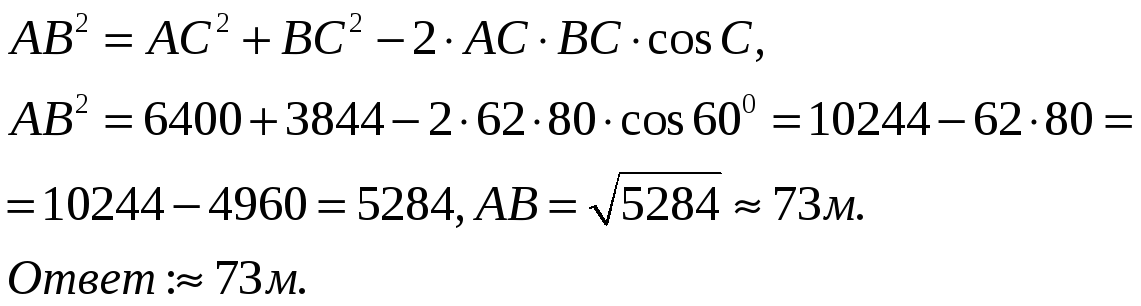
Учитель: Подведем итог урока, ответим на вопросы:

1. Что называют решением треугольников?

2. Какие теоремы применяются при решении треугольников?

3. Чему равна сумма углов треугольника?

4. Какие задачи при этом можно выделить? (по стороне и двум прилежащим к ней углам; по двум сторонам и углу между ними; по трём сторонам; по стороне, прилежащему к ней углу и стороне противолежащей данному углу) (слайд 19)

5. Запишите, пользуясь теоремой косинусов, квадрат стороны с треугольника АВС, если: 1) 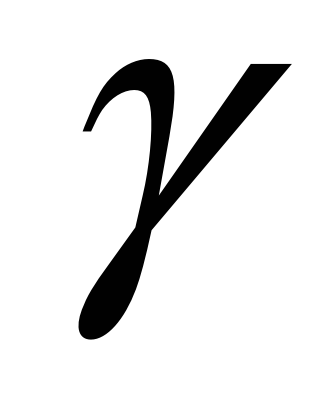=60⁰; 2) 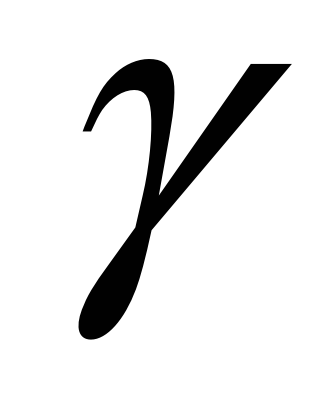=30⁰; 3) 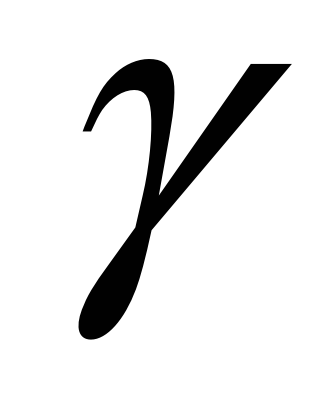=45⁰. (с²=а²+в²-ав; с²=а²+в²-ав; с²=а²+в²-ав)

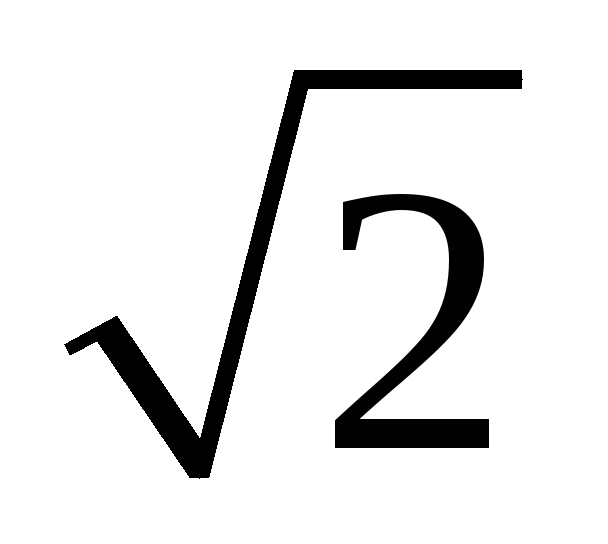6. Чему равен ? ()

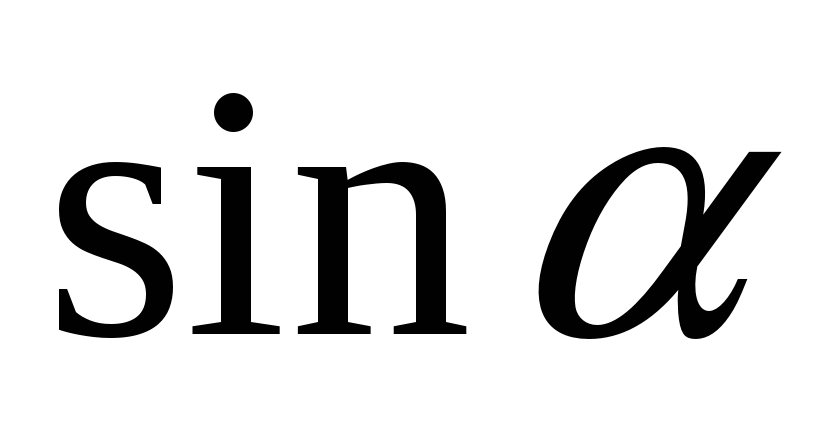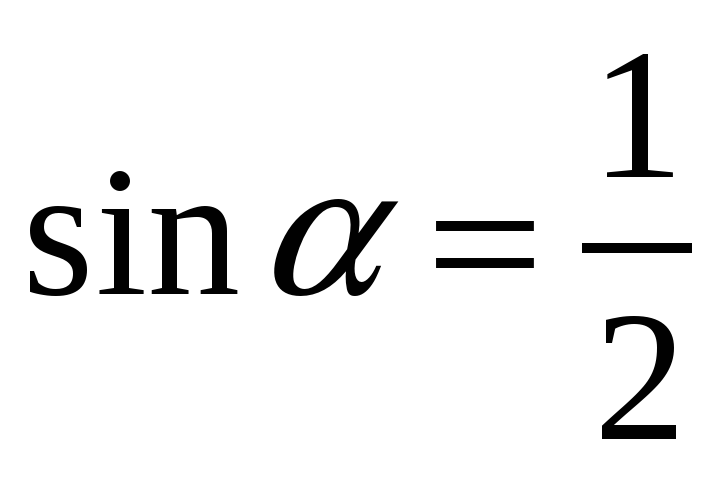7. . Каким может быть ? Ответ: =30⁰ или =150⁰.

1) 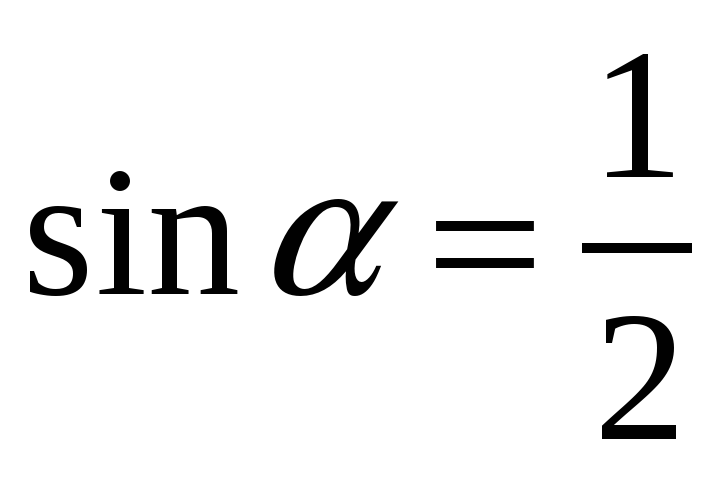, 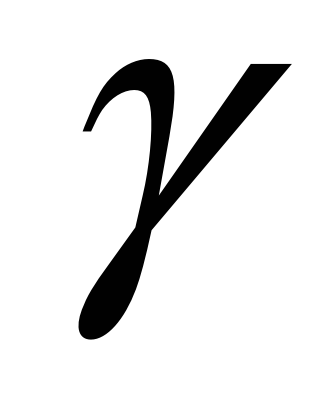- тупой. Тогда =30⁰;

2) 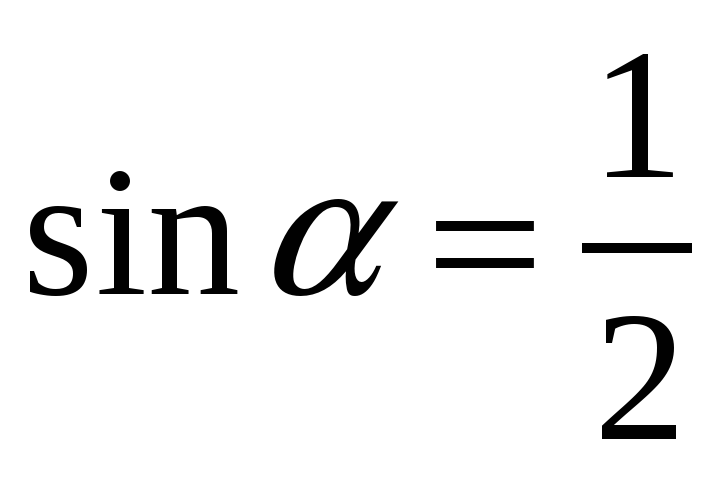, аb, то =30⁰;

3) 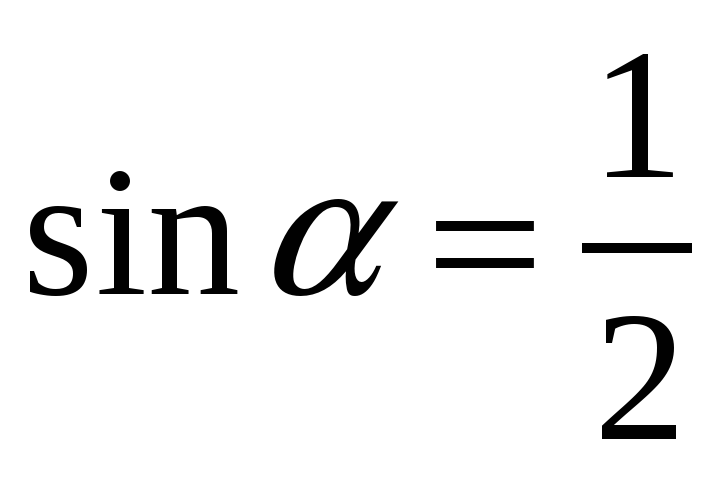, а c, то =30⁰ или =150⁰.

8. Почему теорема косинусов является обобщённой теоремой Пифагора?

(когда треугольник АВС прямоугольный с прямым углом при вершине С; ).

9. Как, используя теорему косинусов определить вид треугольника? (достаточно определить знак косинуса, соответствующего наибольшему углу, если сторона а наибольшая, то достаточно определить знак величины в²+с²-а²)

10. В треугольнике АВС, АВ=8,4 cм, ВС=13,2 см, АС=7,5 см. Какой угол треугольника наибольший, какой наименьший?

11. Стороны треугольника 12см, 15см, 9см. Может ли угол, противолежащий стороне 9см, быть тупым? Почему?

12. Стороны треугольника 9см и 12см. Может ли угол, противолежащий стороне равной 9см, быть прямым? Почему?

Итак, где можно применить полученные знания на практике и в жизни.

Ученик: Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Ученик: Треугольник

В старших классах каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы - на века.

Учитель: Сегодня мы с вами обобщили тему «Решение треугольника». Узнали много интересного из истории развития тригонометрии как науки, кроме того узнали где можно применить полученные знания на практике и в жизни. Запишите домашнее задание.

Спасибо за урок!

Выполнила:

Карабетова М.Е.

учитель математики

МБОУ Хатажукаевская

СОШ№ 6 им. А.Хаткова

а.Пшичо

Шовгеновского района

.

- Знать определения синуса, косинуса, тангенса, котангенса.

- Знать теорему о площади треугольника, теорему синуса, теорему косинуса.

- Уметь решить треугольник, по каким - нибудь трем данным элементам, определяющим треугольник.

- Уметь применять основные формулы раздела при решении задач.

Решение задач.

Практическая работа.

Историческая справка

Актуализация

имеющихся знаний

Реши сам

Разминка

Где можно применить

полученные знания

на практике

в жизни.

Домашнее

задание

слайд 4

β

c

a

α

b

слайд 6

5 см = 0,05 м

x

sin α =

0 , 05

α

х = 0,05 • sin α

слайд 7

3

cos α =

x

3

х =

cos α

α

x

tg α =

2

x = 2 tg α

α

слайд 9

х 2 = АВ 2 +ВС 2 - 2•АВ•ВС • со s 60º

х 2 = 4+9 - 12 • ½ = 13 – 6 = 4

х = 2

60 º

слайд 10

10

х

=

sin 60 º

sin45º

10 •√ 6

10 • sin45º

10 •√2 • 2

=

х =

=

sin 60 º

3

√ 3 • 2

60 º

45 º

слайд 11

√ 2

S = ½ • АС • ВС • sin 45º = ½ • 5 • 2

= 5

2

√ 8

45 º

слайд 12

‹ С = 180º - ‹А - ‹В = 80º

1)

с sin А

14 sin 60º

14 • 0,8660

=

≈ 12,31

2)

а =

≈

sin С

0,9848

sin 80º

60 º

40 º

с sin В

14 • 0,6428

14 sin40º

≈

≈ 9,14

=

b =

3)

sin80º

sin С

0,9848

слайд 13

1) sin В/ b = sin А/а

sin В = b • sin А/а = 10• sin 80º/16 ≈ 0,6155

2) ‹В1 = 37º 59 

‹ В2 = 142º1 

a

так как ‹А + ‹В2 › 180º,

то ‹В = ‹В1 = 37º 59 

3) ‹С = 180º - ‹А - ‹В = 62º1 

80 º

b

4) с = а sin С/ sin А = 16 sin 62º1 / sin 80º ≈ 14,35

слайд 16

1) sin β/ b = sin α/а

sin β = b • sin α/а = 8 sin 30º/6 ≈ 0,667.

2) ‹β 1 ≈ 42º и ‹β 2 ≈138º

30 º

b

3) ‹γ 1 = 180º - α – β ≈108º

с 1 = а • sin γ 1 / sin α ≈ 6 • 0,951 / 0,500 ≈ 11,4

4) ‹γ 2 = 180º - α – β ≈12º

с 2 = а • sin γ 2 / sin α ≈ 6 • 0,2079 / 0,500 ≈ 2,49

β

α

α

А

В

Измерили дальномером расстояние:

СВ = 62 м,

СА = 80 м,

‹ С = 60 º

С

АВ = √ 5284 ≈ 73 м

Типы задач:

- по стороне и двум прилежащим к ней углам;

- по двум сторонам и углу между ними;

- по трём сторонам;

- по стороне, прилежащему к ней углу

и стороне противолежащей данному углу.