6 Кручение

ГПОУ «Читинский техникум отраслевых технологий и бизнеса»

Лекция по технической механике

«Кручение»

Разработчик: преподаватель Батуев Б. Н.

Чита 2015 г

КРУЧЕНИЕ

Это вид деформации, при ко­тором в любом поперечном сечении бруса возникает только крутящий момент.

Деформации кручения возникают, если к прямому брусу в плоскостях, перпендикулярных оси, приложить вращаю­щий момент Т.

На кручение работают валы, имеющие круглое или кольцевое сечение, то рассмотрим кручение круглого цилиндра (рис.).

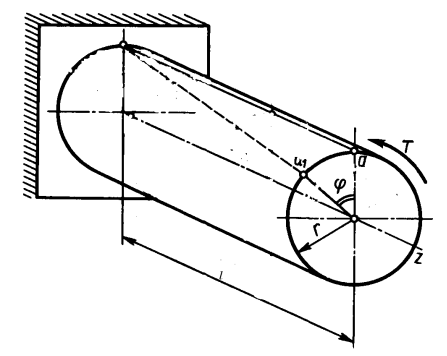
T – вращающий момент

l – длина

При кручении под действием Т:

1. ось = const прямолинейна;

2. d и l = const;

3) образующие цилиндра изменяются по винтовой линии.

Т.е. происходит поворот поперечных сечений относительно друг друга вокруг оси кручения, углы поворота прямо пропорциональны расстояниям от закреп­ленного сечения.

φ – полный угол закручивания.

φ₀- относительный угол закручивания.

φ₀ = φ / l .

При кручении возникает деформация сдвига в результате вращательного движения одного поперечного сечения относительно другого.

Т.е. в поперечных сечениях возникают только касательные внутренние силы - крутящий момент М_к.

Эпюры М_к

Мк в любом поперечном сечении = алгебра­ической сумме внешних моментов, приложенных к брусу справа или слева от сечения.

Эпюры крутящих моментов дают возможность определить опасное сечение. Если брус имеет постоянное поперечное сечение, то опасными будут сечения на участке, где возникает Мк = max.

Мк 0, если при взгляде со стороны сечения M направлен против часовой стрелки, и наоборот.

В поперечном сечении, где приложен Mк, его значения меняются скачкообразно.

Пример.

Дано: Т₁= 500Н∙м,

Т₂ = 150Н∙м,

Т₃= 250 Н∙м,

Т₄=100 Н∙м.

Эпюра Мк - ?

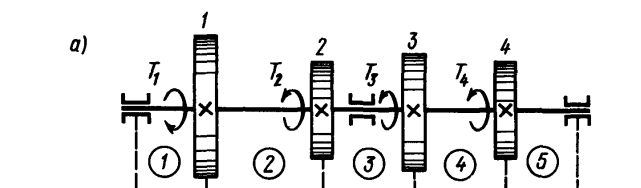
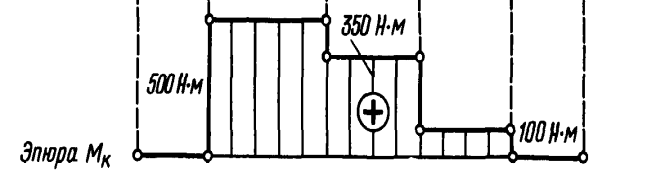
Решение. 1) Разбиваем вал на участки 1 – 5 и применяем метод сечений.

Из эпюры видно, что наибольший крутящий момент на втором участке:

М_{к max} = M_к2 = 500Н∙м, т.е является опасным участком.

Напряжения и деформации

Каса­тельные напряжения максимальны в наибольшей удаленности от оси кручения:

τ_mах = G φ₀ r.

Эпюра распределения напряже­ний вдоль радиуса сечения имеет вид треугольника (рис.).

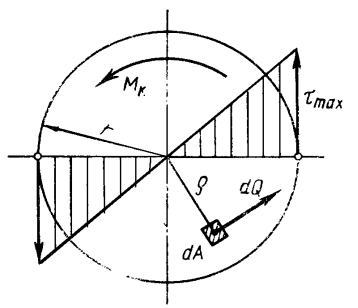
Крутящий момент: М_к = G φ₀ I_p,

Oткуда: φ₀ = М_к /( G I_p), рад.

φ = М_к l/( G I_p), рад.

где GI_p – жесткость сечения.

Т.о. полный угол закручивания круглого цилиндра прямо пропорционален крутящему моменту, длине цилиндра и обратно пропорционален жесткости сечения при кручении.

Для бруса, имеющего несколько участков: φ = ∑ φ_i

где φ_i – угол закручивания каждого участка.

Формула напряжений:

τ_max = М_кr/I_р = М_к/(I_р/r) = М_к/W_р,

где W_р = I_р/r — момент сопротивления кручению (или полярный момент сопротивления), в м³.

Момент сопротивления кручению:

1. Круг Wp ≈ 0,2d³.

2. Кольцо Wp ≈ 0,2(D⁴-d⁴)/D.

Пример.

Дано: Стальная круглая проволока длиной l=1 м, диаметром d=2 мм одним концом укреплена в зажиме, а на другом конце к ней приложен скручивающий момент. При каком угле закручивания напряжение кручения будет равно 60 МПа? Модуль упругости G = 8,2∙10⁴ МПа.

φ - ?

Решение. Запишем формулы, необходимые для решения задачи: полный угол закручивания круглого цилиндра φ = М_кl/(GI_р);

максимальное напряжение при кручении

τ_max = М_к/ W_р,

откуда М_к = τ_mах W_р .

Учитывая, что полярный момент инерции

I_p = W_p∙d/2

и подставляя числовые значения, получим

φ = τ_mахW_рl∙2/(GW_рd) = τ_mахl∙2/(Gd)= 60∙10⁶∙1∙2/(8,2∙10⁴∙10⁶∙2∙10^-3) = 0,732рад ≈42°.

Расчетные формулы на прочность и жесткость при кручении

Условие прочности

Расчетная формула на прочность при кручении:

τ_k = М_к/W_p ≤ [τ_k]

и читается так: касательное напряжение в опасном сечении, вычисленное по формуле τ_k = М_к/W_p не должно превышать допускаемое.

Допускаемое напряжение при кручении выбирают в зависи­мости от допускаемого напряжения при растяжении, а именно:

для сталей [τ_к] = (0,55... 0,60) [σ_р];

для чугунов [τ_к] = (1...1,2)[σ_р].

Кроме прочности к валам предъявляется требование

условия жест­кости: заключающееся в том, что угол закручивания 1 м длины вала не должен превышать допустимой величины во избежание, например, пружинения валов или потери точности ходовых винтов токарно-винторезных станков.

Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ₀^°];

расчетная формула на жесткость при кручении:

φ₀^° = (180°/π)(M_k/GI_p)≤ [φ₀^°].

Величины допускаемых углов закручивания зависят от назначения вала; их обычно принимают в следующих пределах:

[φ₀^°] = 0,25...1 град/м.

С помощью этих формул выполняют три вида расчетов конструкций на прочность и жесткость при кручении — проектный, проверочный и определение допуска­емой нагрузки.

***

Список использованных источников

1. Атаров Н.М. Сопротивление материалов в примерах и задачах. М.: Инфра-М, 2010.

2. Ксендзов В.А. Техническая механика. М.: КолосПресс, 2010.

3. Эрдеди А.А. и др. Теоретическая механика. Сопротивление материалов: /А.А.Эрдеди, Ю.А.Медведев, Н.А.Эрдеди. – М.: Высш. шк., 2001.