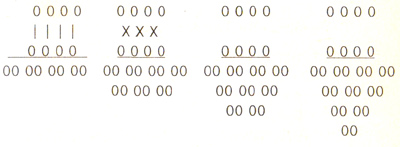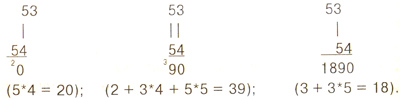1. Старинные способы вычисления
1.1 Древний счёт
Вначале древние люди могли считать не больше, чем до трех. У них были три слова, обозначавшие "один", "два" и "много". Потом они научились считать до пяти, по кол-ву пальцев на одной руке, потом до десяти, наконец до двадцати (складывая пальцы еще и на ногах). Потом начали использовать для счета камешки. В основном счет был необходим для торговли между племенами.
Но потом дальнейшее развитие счета надолго затормозилось (чуть ли не до возникновения письменности).
Греки применяли несколько способов записи чисел. При использовании ионической нумерации числа выражались буквами алфавита. Чтобы отличить число от слова, над буквами числа ставился специальный значок  -титло. Этот способ записи чисел применялся жителями Милета и Александрии. Афиняне для обозначения чисел пользовались первыми буквами слов-числительных:
-титло. Этот способ записи чисел применялся жителями Милета и Александрии. Афиняне для обозначения чисел пользовались первыми буквами слов-числительных:
Г (Γέύτέ) - пять,
Δ(Δέκά)- десять,
Χ(Χιλιάό) - тысяча,
Μ(Mυριάό) - десять тысяч,
I, II, III, IIII - соответственно 1, 2 , 3, 4
ΔΔΔIIII - 10+10+10+4=34

1.2. Русский крестьянский способ умножения
В России несколько веков назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название КРЕСТЬЯНСИЙ (существует мнение, что он берет начало от египетского).
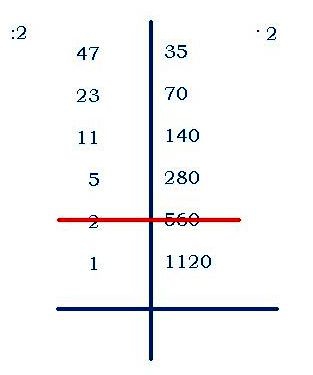
Пример: умножим 47 на 35:
запишем числа на одной строчке, проведём между ними вертикальную черту;
левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
деление заканчивается, когда слева появится единица;
вычёркиваем те строчки, в которых стоят слева чётные числа; 35 + 70 + 140 + 280 + 1120 = 1645
далее оставшиеся справа числа складываем – это результат.
2 . Способы устного счёта
2.1 Сложение
1. Промежуточное приведение к «круглым» числам
Если хотя бы одно слагаемое близко к «круглому» числу десятков, сотен, тысяч и т.д. (100, 300, 1000)вычисления можно упростить:
приведя одно из слагаемых к ближайшему «круглому» числу;
выполнив более легкое вычисление с «круглым» и затем учтя поправку.
Пример:
187 + 198 = 187 + (198 + 2) – 2 = 187 + 200 – 2 = 387 – 2 = 385
358 – 197 = 358 – 200 + 3 = 158 + 3 = 161.
2. Способ «корневых» чисел
При обработке статистических измерений иногда приходится складывать числа, «скапливающиеся» около одного «корневого» числа, на глаз близкого к среднему. Разумно провести такое сложение в три приема:
найти сумму «корневых чисел»;
найти сумму отклонений каждого числа от «корневого»;
полученную сумму алгебраически (с учетом знака) прибавить к итогу пункта «1».
Пример:
37 + 34 + 33 + 35 + 34 + 33 + 34 = 34*7 + (3 + 0 – 1 + 1 + 0 – 1 +0) = 238 + 2 = 240
2.2 Вычитание
Переход от вычитания к сложению
Обычно человеку гораздо легче складывать, нежели вычитать. Этим часто можно пользоваться, при этом из уменьшаемого вычитается круглое число, а затем прибавляется поправка:
3117 - 53 = 3117 - 100 + 47 = 3017 + 47 = 3064
Промежуточное приведение к "круглым" числам
Если одно из слагаемых близко к круглому числу, то часто бывает полезно округлить его, а затем учесть поправку:
198 + 53 = (200 - 2) + 53 = 200 + 53 - 2 = 253 - 2 = 251
1912 - 207 = 1912 - (200 + 7) = 1912 - 200 - 7 = 1712 - 7 = 1705
2.3 Умножение
1. Умножение "пирамидой"
Этот способ иногда называют также общим способом сокращенного умножения.
Пример:
351 * 248.
1. Умножаем цифры, стоящие друг под другом, выделяя под каждой результат по 2 знака.
2. Умножаем накрест соседние цифры. Итог пишем со сдвигом на 1 знак влево под результатом 1-го шага.
3. "Раздвигаем" шаг креста на одну позицию. Под него попадают только крайние цифры. Записываем их произведение под результатом предыдущего шага со сдвигом на 1 знак влево:

На практике промежуточные итоги, разумеется, суммируются, не дожидаясь окончания вычислений после каждого шага. Для чисел большей значности схема выглядит аналогично
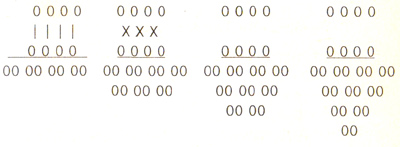
2. Способ обращения и сдвига
-При выполнении вычислений по двум вышеприведенным способам иногда возникает пожелание, сохранив их преимущества, избавиться от необходимости "прыгать по крестам". Оказывается, для этого достаточно развернуть один из сомножителей вокруг своей младшей цифры (переписать в обратном порядке) и сдвигать их в таком виде друг относительно друга, находя суммы перемножений соседей по вертикали. Этот способ так и называется — способ сдвига, а работает он следующим образом.
Пример:
35 * 54 преобразуем как 53
* 54
Производим вычисления:
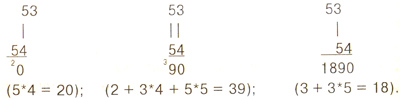
Не забудьте, что выбранный вами сомножитель обращают вокруг самой младшей цифры!
3. Способ изменения сомножителей
Если один из сомножителей увеличить в М раз, а второй во столько же раз уменьшить, итог не изменится, однако умножение может стать проще и быстрее.
Примеры:
24 * 25 = (24:4) * (25*4) = 6 * 100 = 600;
17 * 12 = (17*3) * (12:3) = 51 * 4 = 204.
При этом сведение одного из множителей к однозначному числу - лишь частный случай, скажем: 28*55 = (28:2) * (55*2) = 14*110, что вычислять уже легче.
Если же один из множителей - это 5*10n; 25*10n; 125*10n, соответственно умножаем другой сомножитель на 2;4;8 и делим другой на то же число:
256 * 5 = (256:2) * (5*2) = 128 * 10 = 1280;
35 * 25 = 35:4 * 25*4 = 3500 : 4 = 875;
48 * 125 = 48:8 * 125*8 = 6*1000 = 6000.
При делении на 5 * 10n; 25 * 10n; 125 * 10n используем те же свойства:
120 : 25 = 120*4 : 25*4 = 480 : 100 = 4,8.
2.3 Деление
1. Разложение делимого на слагаемые. Разложение делимого на такие слагаемые, которые легко бы делились раздельно, ускоряет устный подсчет числа при делении.
Пример. Найдем частное чисел 2 808 и 9.
Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 / 9) = 300 + 10 + 2 = 312.
2Деление на единицу с последующими нулями. При делении на 10; 100; 1 000 как целого числа, так и дробного в нем отделяют запятой справа налево столько десятичных знаков, сколько нулей стоит в делителе после единицы.
Пример. Найдем частное от деления чисел 136 на 10, 32,7 на 1000.
Решение. 136 / 10= 13,6;32,7 / 1 000 = 0,0317.
3Деление на 0,5; 0,25; 0,125. Десятичную дробь 0,5 заменяют простой, т.е. 1/2. Чтобы разделить какое-то число на 0,5, необходимо умножить его на 2.
Пример. Разделим число 325 на 0,5.
Решение. 325 / 0,5 = 325 / 1/2 = 325 х 2 = 650.
При делении числа на десятичную дробь 0,25 ее заменяют простой дробью, т.е. 1/4. Чтобы разделить какое-то число на 0,25, необходимо умножить его на 4.
Пример. Разделим число 325 на 0,25.
Решение. 325 / 0,25 = 325 x 4 = 1300.
При делении десятичную дробь 0,125 заменяют простой, т.е. 1/8. Чтобы разделить какое-то число на 0,125, необходимо умножить его на 8.
Пример. Разделим число 325 на 0,125.
Решение. 325 / 0,125 = 325 x 8 = 2600.