Сравнение десятичных дробей

Сравнение десятичных дробей

Устные задания:

Сколько единиц в каждом из разрядов в числе:

1) 16

1 десяток 6 единиц

2)234

2 сотни 3 десятка 4 единицы

4 единицы 7 десятых

3)4,7

5 десятков 2 единицы 6 десятых 8 сотых

4)52,68

5)10,19

1 десяток 1 десятая 9 сотых

6)3,507

3 единицы 5 десятых 7 тысячных

7)506,0506

5 сотен 6 единиц 5 сотых 6 десятитысячных

8)78,1002030

7 десятков 8 единиц 1 десятая 2 десятитысячных 3 миллионные

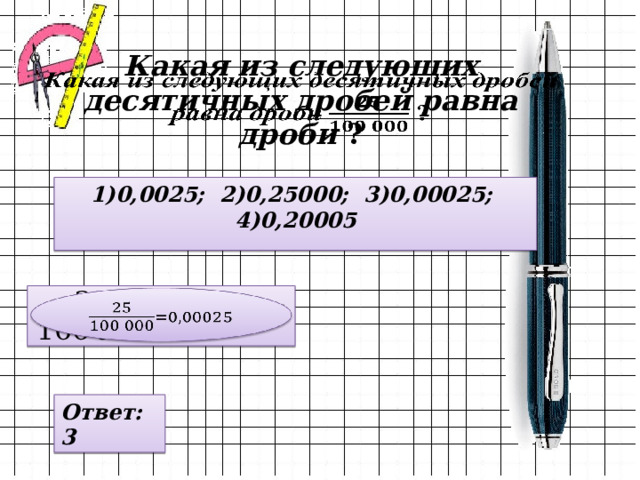
Какая из следующих десятичных дробей равна дроби ?

1)0,0025; 2)0,25000; 3)0,00025; 4)0,20005

Ответ: 3

Какое из чисел больше: 5,3 или 4,988?

Из двух десятичных дробей больше та, у которой целая часть больше.

Значит: 5,3  4,988

Как сравнить дроби с равными целыми?

В этом случае вначале сравнивают десятые.

Например, 11, 2 3  11, 1 9, так как 2  1.

Если же десятые оказались одинаковыми, то сравнивают сотые.

Например, 2,8 4  2,8 6 , так как 4  6.

Такой способ сравнения десятичных дробей называют поразрядным.

Как сравнить десятичные дроби с равными целыми частями, но с различным количеством цифр после запятой?

Сравним отрезки длиной 5,4 м и 5,40 м. Имеем:

5,4 м = 5м = 5 м 4 дм = 540 см;

5,40 м = 5 м = 5 м 40 см=540

Получаем, что 5,4=5,40

Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной.

Значение дроби, оканчивающейся нулями, не изменится, если последние нули в её записи отбросить.

Сравним дроби 3,2 и 3,198.

Поскольку, 3,2=3,200, а 3,200  3,198,то 3,2  3,198

Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.

№ 820: запишите десятичную дробь:

1) С двумя цифрами после запятой, равную числу 0,4

2) С четырьмя цифрами после запятой, равную числу 3,26

3) С тремя цифрами после запятой, равную числу 42

4) С двумя цифрами после запятой, равную числу 18,50000

0,40

3,2600

42,000

18,50

№ 821: запишите несколько десятичных дробей, равных данной :

5,400 = 5,40000 = 5,40 = 5,4

• 5,400

• 12,5080

• 0,980

12,5080 = 12,50800 = 12,508

0,980 = 0,9800 = 0,98

№ 822: уравняйте количество цифр после запятой в данных дробях:

• 2,16; 18,5; 0,476; 1,4;

2) 8,1; 19,64; 5,345; 0,9872;

2,160; 18,500; 0,476; 1,400

8,1000; 19,6400; 5,3450; 0,9872

№ 823(1-3) сравните числа:

• 9,4 и 9,6;

• 5,5 и 4,8;

• 6,3 и 6,31







№ 825: запишите числа в порядке убывания: 8,5; 8,16; 8,4; 8,49; 8,05; 8,61.

8,61

8,5

8,49

8,4

8,16

8,05

№ 209: сравните числа:



• 6,7 и 6,8

• 5,4 и 4,9

• 12,4 и 12,42

• 26,39 и 26,276

• 0,4 и 0,09

• 5,1 и 5,098











№ 210: расположите числа в порядке возрастания: 7,4; 3,15; 3,6; 5,066; 5,2; 7,28.

7,4

7,28

5,2

5,066

3,6

3,15

Найдите все натуральные значения х , при которых верно неравенство:

Х: 4; 5; 6

• 3,54  х  6,001;

• 8,9  х  12;

Х:9; 10; 11

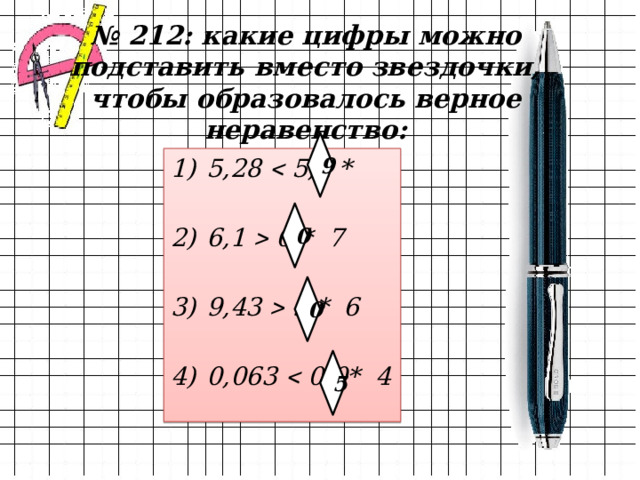
№ 212: какие цифры можно подставить вместо звездочки, чтобы образовалось верное неравенство:

9

• 5,28  5,2 *

• 6,1  6,* 7

• 9,43  9,* 6

• 0,063  0,0* 4

0

0

5

№ 213: напишите три числа, каждое из которых больше 7,5 и меньше 7,7 .

7,7

7,5

7,6

7,55

7,65

Какая из двух десятичных дробей с неравными целыми частями больше?

Из двух десятичных дробей больше та, у которой целая часть больше.

Как сравнивают десятичные дроби с равными целыми частями и одинаковым количеством цифр после запятой?

Десятичные дроби с равными целыми частями и одинаковым количеством цифр после запятой сравнивают поразрядно.

Какую дробь мы получим, если к данной десятичной дроби припишем справа несколько нулей?

Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной.

Какую дробь мы получим, если у данной десятичной дроби отбросим последние нули её записи?

Если десятичная дробь оканчивается нулями, то эти нули можно отбросить, и при этом получится дробь равная данной.

Сформулируйте правило сравнения двух десятичных дробей с равными целыми частями и различным количеством цифр после запятой.

Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, нужно с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.

Домашнее задание:

§ 31, вопросы 1-5, № 824, 826,839