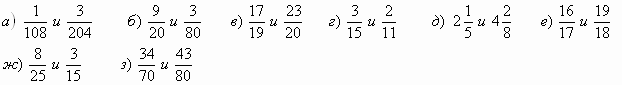Урок №42 МАТЕМАТИКА 6 КЛАСС
ТЕМА УРОКА: «СРАВНЕНИЕ И УПОРЯДОЧИВАНИЕ ДРОБЕЙ.» ДАТА: 07.11.2023
Тип урока: урок усвоения новых знаний
Цели урока:
Обучающие:
выработать умения применения правил сравнения дробей с одинаковыми знаменателями и с одинаковыми числителями;
проверить первичные знания учащихся по теме «С равнение дробей».
Развивающие:
развивать внимание, логическое и математическое мышление, вычислительные навыки. умение анализировать, математические и коммуникативные компетенции, интерес к предмету;
расширять кругозор учащихся.
Воспитательные: воспитывать:
аккуратность;
целеустремленность;
доброжелательное отношение друг к другу.
побуждать учеников к взаимоконтролю, вызывать потребность в обосновании своих высказываний.
Универсальные учебные действия
Познавательные: строят речевое высказывание в устной и письменной форме.
Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи
Коммуникативные: вступают в речевое общение, участвуют в диалоге.
Личностные: проявляют познавательный интерес к изучению предмета.
ХОД УРОКА
1. Организационный момент.
- Здравствуйте ребята! Сегодня у нас необычный урок.
Все мы разные и вместе с тем очень похожие. Давайте это проверим.
Кому нравится кататься на велосипеде, поднимите правую руку. Кто любит плавать, покажите левую ладонь. Кому понравились зимние каникулы, хлопните в ладоши. Все, у кого есть друзья, улыбнитесь.
Как видите, мы лучше узнали друг друга. Сегодня на уроке мы будем работать вместе, и я рассчитываю на плодотворную и успешную работу.
Начнем с устной работы.

2. Устная работа.
«Помоги жеребенку перебраться на другой берег».(слайды)
3.Актуализация опорных знаний учащихся
1. Прочитайте дроби, назовите числитель и знаменатель дроби (Слайд)
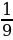 ,
, 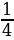 ,
, 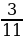 ,
, 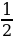 ,
, 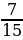 ,
, 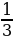 ,
, 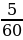
Что показывает числитель? Что показывает знаменатель?
2.
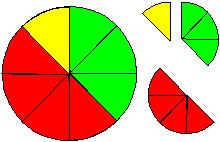
Какая часть круга закрашена желтым цветом? (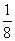 )
)
Какая часть круга закрашена зеленым цветом? ( )
)
Какая часть круга закрашена красным цветом? (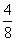 )
)
4. Изучение нового материала
1)( Проблемная ситуация).
Прочитайте числа в порядке возрастания:
679,504,398,276,985,414.
- А теперь вторую группу чисел в порядке возрастания прочитайте:
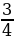 ,
, 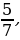
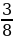 ,
, 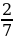 .
.
-? Можем? Нет . А почему? Нужно сравнивать , а мы не умеем – как.
2) формулировка темы и цели урока
Вот сегодня мы с вами и займемся этим. Так кто же сформулирует тему урока?
Тема урока «Сравнение дробей», запишите в тетради.
На слайде тот же ряд дробей: 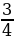 ,
, 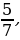
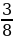 ,
, 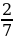 .
.
− На какие группы можно разбить все дроби? (Дроби, у которых одинаковые числители, дроби, у которых одинаковые знаменатели.)
На слайде:
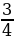 и
и 
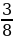

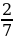
− Назовите знаменатели дробей первой группы.
− Что показывает знаменатель дроби? (Знаменатель показывает, на сколько равных частей разделено целое.)
− Назовите числители дробей второй группы.
− Посмотрите на эти дроби и скажите, какой знак сравнения нужно поставить вместо буквы «и»?
- Почему возникли затруднения? (Не знаем способа сравнения дробей.)
4. Построение проекта выхода из затруднения.
− Сформулируйте цель вашей деятельности. (Узнать способ сравнения дробей.)
− Какие дроби входят в каждую группу? (В первую группу входят дроби с одинаковыми числителями, а во вторую с одинаковыми знаменателями.)
− По какому признаку будем сравнивать дроби? (По одинаковым числителям или одинаковым знаменателям.)
− Уточните цель вашей деятельности. (Построить правило сравнения дробей с одинаковыми числителями и правило сравнения дробей с одинаковыми знаменателями.)
− Открывать знания вы будете в парах.
Одни пары будут работать с первой группой дробей, а другие – со второй группой дробей.
- Я вам раздала по два круга, разделите круги на необходимое количество равных частей, покрасьте то количество частей, которое соответствует числителям дробей, сравните, закрашенные части, сделайте вывод, сформулируйте правило.
(Правило сравнения дробей с одинаковыми числителями.)
(Правило сравнения дробей с одинаковыми знаменателями.)
5. Реализация проекта выхода из затруднения.
Учащиеся работают по реализации плана самостоятельно. Потом озвучивают правило.
Вывод 1:
Из двух дробей с одинаковыми числителями та дробь больше (меньше), знаменатель, которой меньше (больше).
Вывод 2:
Из двух дробей с одинаковыми знаменателями та дробь больше (меньше), числитель, которой больше (меньше).
− Теперь вы сможете ответить на вопрос: какой знак нужно поставить между дробями?
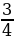

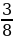
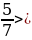
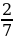
5.Физминутка
(Супер физминутка)
6. Закрепление новых знаний
1.Работа по карточкам №1 Сравнить дроби (выходят к доске по одному и записывают выражение, проговаривая правило.)

 и
и 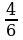 ;
; 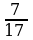 и
и 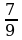 ;
;
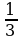 и
и 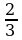 ;
; 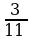 и
и 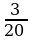 .
.
2.Выполнить из учебника №947
7. Самостоятельная работа с самопроверкой
− А теперь проверьте, как каждый из вас понял, применения правила сравнения дробей.
Подпишите фамилию .
Сравнить дроби:

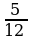 и
и 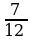 ;
;  и
и 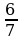 ;
;
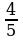 и
и  ;
; 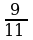 и
и 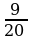 .
.
После выполнения задания, учащиеся сопоставляют свои работы с эталоном для самопроверки
| 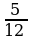 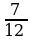
| Равны знаменатели. 5 7 |
| 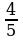 
| Равны знаменатели. 4 2 |
|  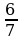
| Равны числители. 19 7 |
| 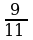 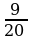
| Равны числители. -
20 |
-
Выполнение заданий для повторения.
№959, №960
-
Подведение итогов урока.
-Что изучили сегодня на уроке?
-Кто желает сформулировать правила сравнения обыкновенных дробей?
Оценить отдельных учащихся
-
Домашнее задание
-
карточка
-
Ответить на вопрос: в каком мешке больше?
4/5 3/4


-
Рефлексия деятельности на уроке.
− Что нового вы сегодня узнали? (Мы узнали правила сравнения обыкновенных дробей с одинаковыми числителями и с одинаковыми знаменателями.)
− Оцените свою деятельность на уроке: большой палец вверх, если вы поняли, как сравнивать дроби и в самостоятельной работе не допустили ошибок, или вниз, если вы поняли, как сравнивать дроби, но в самостоятельной работе ошибки были.
-
Учитель благодарит учащихся за плодотворную совместную работу на уроке:
Спасибо, ребята, вам всем за урок,
Пусть все эти знанья будут вам впрок.
Теперь говорю я вам всем “до свидания”,
Окончен урок. Спасибо за вниманье
-
Дополнительно:
-
Учитель - Представьте частные в виде несократимых дробей:
-
5 : 10
-
4 : 6
-
6 : 8
-
8 : 10
-
10 : 12
-
Ученики - 1/2 2/3 3/4 4/5 5/6
-
Учитель - Что вы заметили?
-
Ученики - Числитель дроби на 1 меньше знаменателя.
-
Учитель - Как вы думаете, в каком порядке расположены дроби?
-
Ученики - В порядке увеличения.
-
Учитель - Как доказать?
-
Ученики - Можно привести к одному знаменателю.
-
Учитель - Отметьте эти точки на координатном луче, что вы заметили?
-
Ученики - Чем больше числитель и знаменатель, тем ближе расположено число к 1, т.е. 1/2 отличается от 1 на 1/2, 3/4 отличается от 1 на 1/4, 4/5 отличается от 1 на 1/5
-
1/2 1/3 1/4 1/5 1/6
-
Расстояния до 1 сокращаются, значит, сами числа увеличиваются!
-
Вывод: Обыкновенные дроби можно сравнивать, дополняя их до 1!
-
Учитель - Используя прием сравнения с 1, сравните: 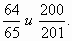
-
Ученики - 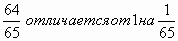
-

-
Учитель - Как легче сравнить эти дроби? Приводя к одному знаменателю, или сравнивая с единицей?
-
Ученики - Конечно, сравнивая с единицей, так как иначе мы столкнемся со сложными вычислениями.
-
Учитель - Проанализируйте высказывание: если 3 · 7 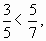 почему оно верно?
почему оно верно?
-
Ученики - Если приводить эти дроби к одному знаменателю, то придется 3 7, а 5 5, затем сравниваем числители.
-
Учитель - Сформулируйте правило в буквенном виде!
-
Ученики - 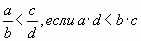
-
Учитель - Это правило называется перекрестным правилом сравнения дробей.
-
Пользуясь этим правилом, сравните:
-
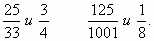
-
Ученики - 25?4 больше, чем 33?3 , значит 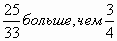 .
.
-
125?8 меньше, чем 1001?1 , значит 
-
Учитель - Придумайте хитрые способы для сравнения дробей. (Ответы учеников указаны в скобках)
-
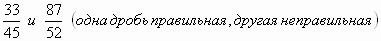
-
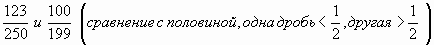
-
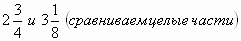

-
4 этап (10 минут)
-
Учитель - Сравните дроби, называя алгоритмы, которыми пользовались при сравнении.
-
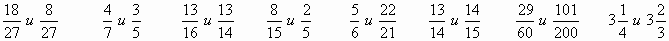
-
Ученики выполняют задание, проговаривая алгоритмы.
-
Учитель - Укажите без преобразований наибольшую и наименьшую из дробей. Расположите дроби в порядке убывания.
-

-
У учащихся возникли затруднения.
-
Ученики - Все дроби больше половины. А как же сравнивать?
-
- А если определить, на сколько каждая дробь отличается от половины и вспомнить прием дополнения до единицы?
-
-Действительно, первая дробь отличается от половины на 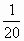 , вторая на
, вторая на 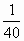 , а третья на
, а третья на 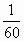 .
.
-
-
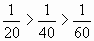 , значит,
, значит, 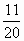 находится на луче правее чем
находится на луче правее чем 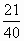 и правее, чем
и правее, чем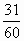 .
.
-
Ответ: а)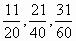
-
Выполняются оставшиеся задания.
-
5 этап (10 минут)
-
Самостоятельная работа с самопроверкой.
-
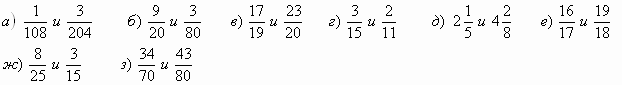
-
При самопроверке учащиеся устанавливают причины затруднений.
-
6 этап (4 минуты)
-
Итог урока
-
Учитель. - Какие хитрые приемы сравнения обыкновенных дробей сегодня на уроке мы вывели?
-
Ученики - сравнение с 1
-
- сравнение с 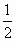
-
- перекрестного умножения.
-
Учитель - Зачем нужны эти правила?
-
Ученики - Чтобы сравнивать дроби можно было проще и быстрее.
-
Учитель прощается с учениками и благодарит их за урок.







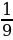 ,
, 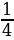 ,
, 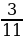 ,
, 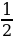 ,
, 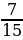 ,
, 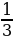 ,
, 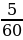

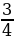 ,
, 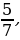
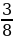 ,
, 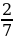 .
.

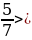

 и
и 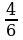 ;
; 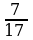 и
и 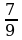 ;
;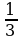 и
и 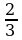 ;
; 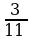 и
и 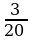 .
.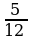 и
и 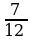 ;
;  и
и 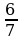 ;
;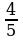 и
и  ;
; 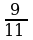 и
и 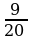 .
.