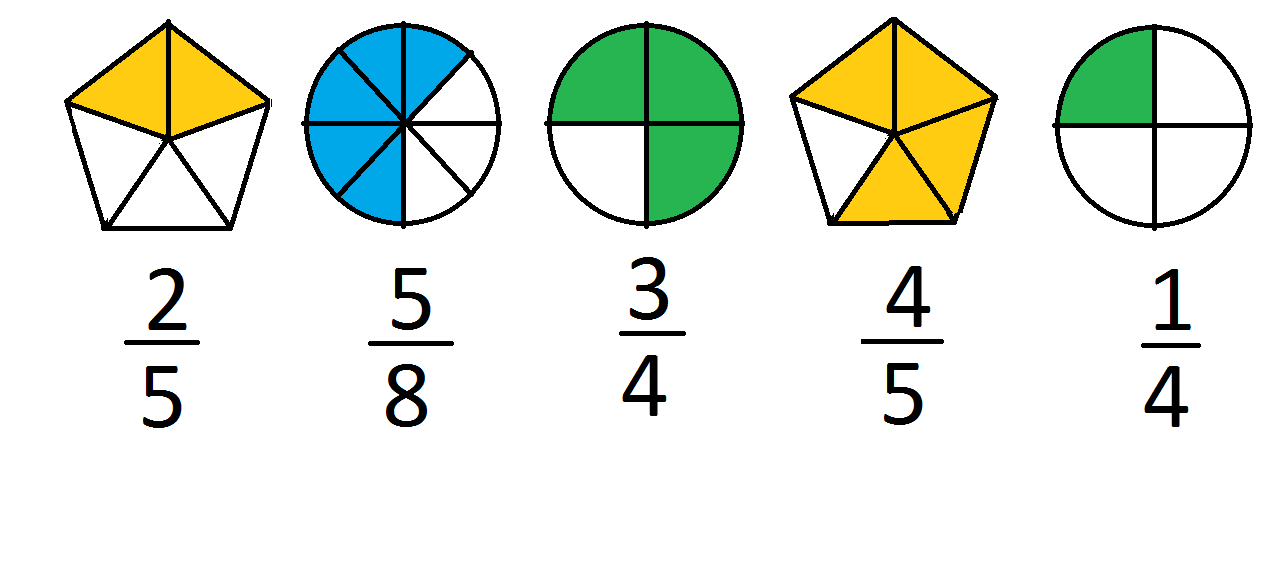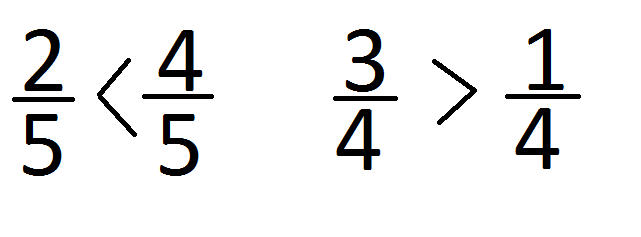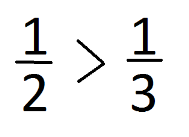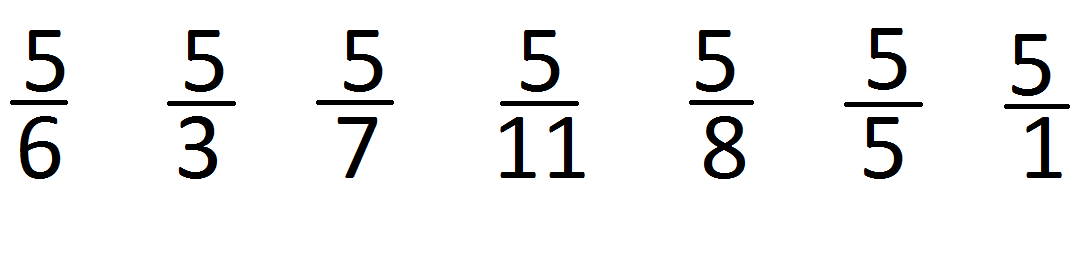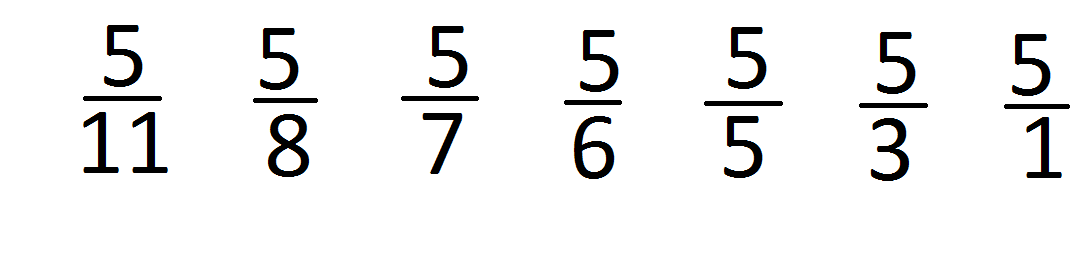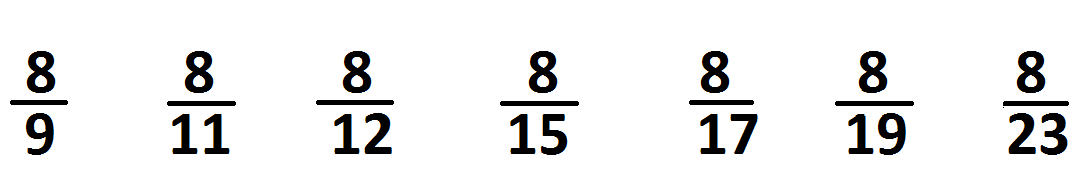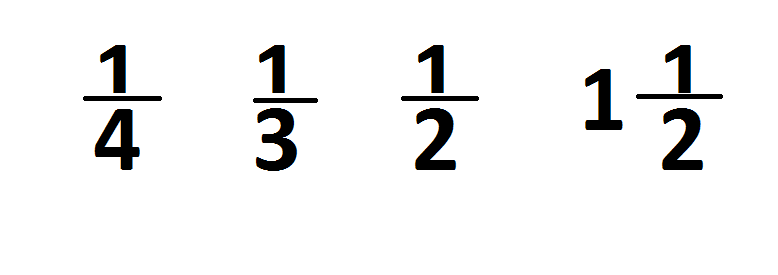План-конспект открытого урока по теме:

Ершова Ирина Васильевна учитель математики
Предмет: математика.
Класс: 5.
Тип урока: изложение нового материала.
Цели урока:
Образовательная: добиться усвоения правила сравнения дробей с одинаковыми числителями;.
Воспитательная: воспитывать трудовые навыки; эстетическое начало; уделить внимание нравственным принципам.
Развивающая: развивать общеучебные навыки анализа, синтеза, классификации, устной речи, самостоятельной работы, работы в группах и коллективе, зрительного представления, творческого воображения, ориентировки в пространстве, повышать общий культурный уровень.
Задачи урока:
- сформировать о представление о зависимости величины дроби от знаменателя;
- добиться усвоения правила сравнения дробей с одинаковыми числителями;
- добиться умения комплексного применения правил сравнения дробей.
Оборудование и пособия: интерактивная доска, слайды, набор «доли и дроби», нотные листки с нанесенной нотной разметкой
Этапы урока.
| 1.Актуализация опорных понятий и вхождение в тему. |
| 2. Целеполагание. |
| 3 Изложение нового материала. |
| 4. Немного философии. |
| 5. Первоначальное закрепление |
| 6. Тренировочное закрепление. |
| 7. Тематическая физкультминутка |
| 8. Задание «музыкальная композиция» |
| 9. Подведение итогов. Измерение достижения цели. |
|
|
Ход урока.
Актуализация опорных понятий.
Организационный момент начала урока. Приветствие.
Интерактивное задание.
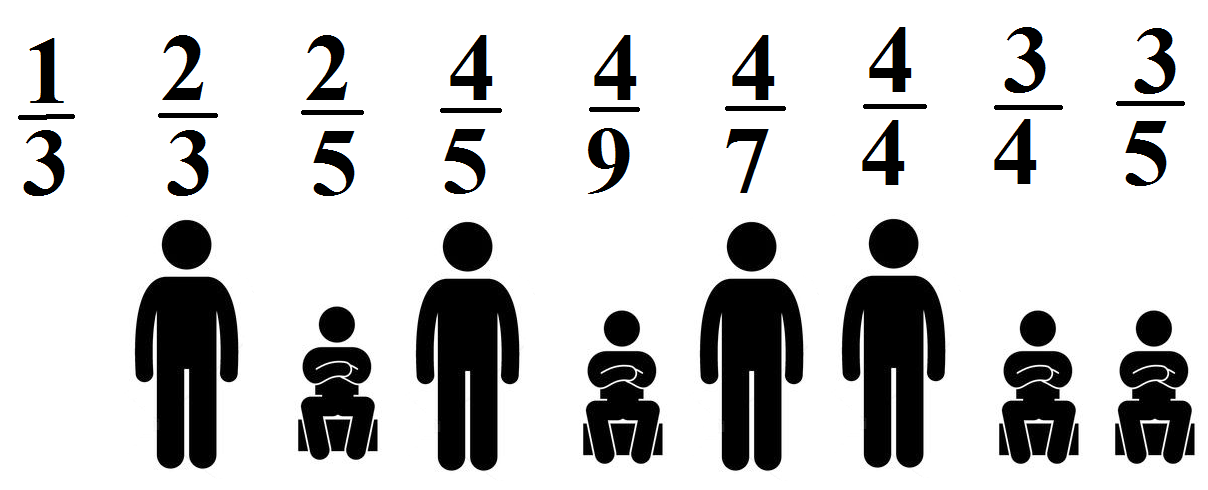
Соотнесите картинки и дроби.
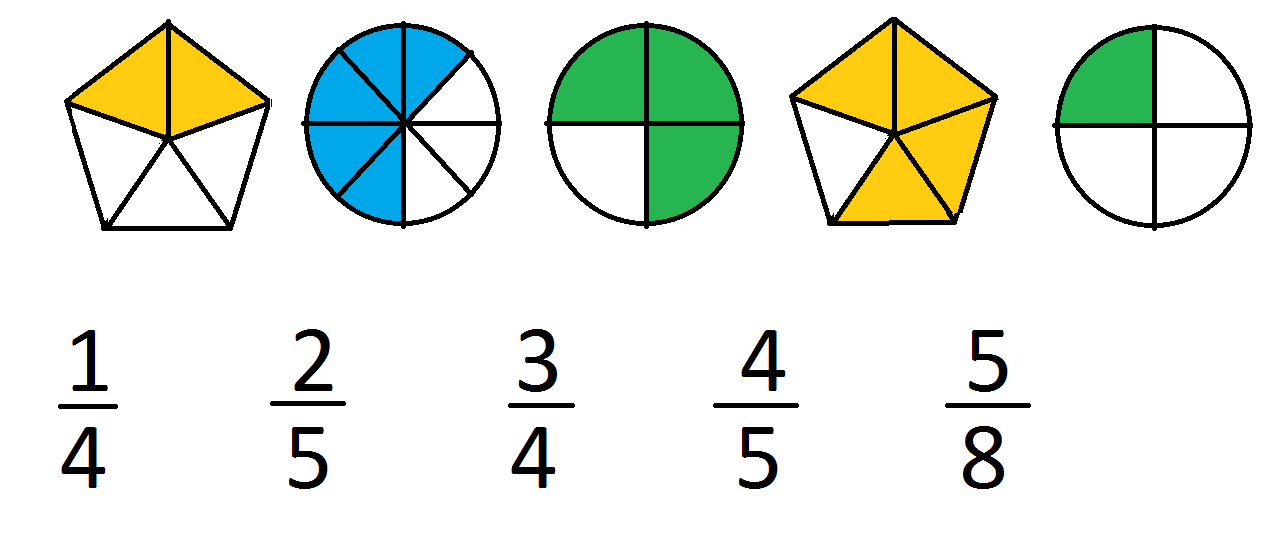
Назовите числитель и знаменатель каждой из дробей.
Ответы:
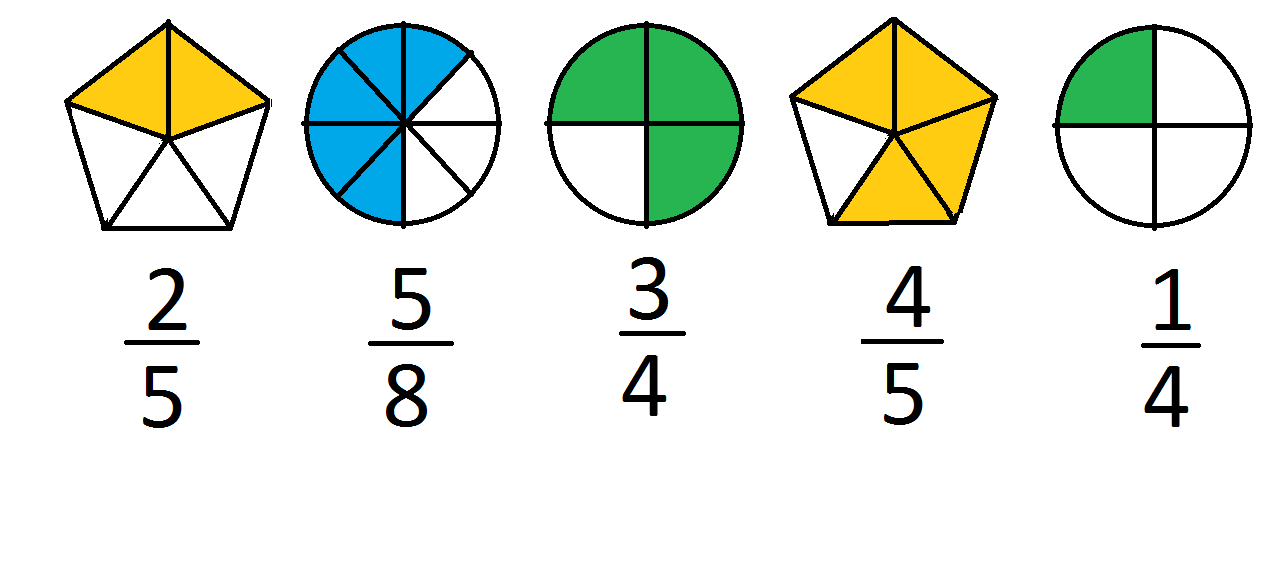
Выпишите пары дробей, изображенных картинкой одинакового цвета и поставьте знак сравнения.
Ответы:
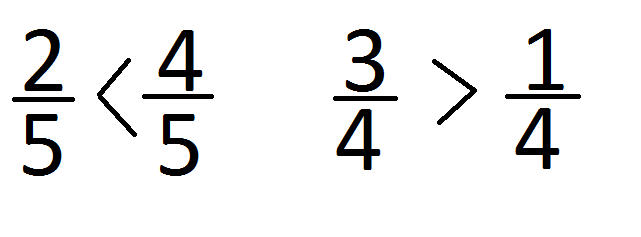
Каким правилом вы при этом пользовались? Вспомните правило сравнения дробей с одинаковыми знаменателями.
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.
Целеполагание .
А теперь давайте сравним следующие дроби.
Что длится дольше: пол-урока или треть урока?
Запишите это в виде неравенства дробей.
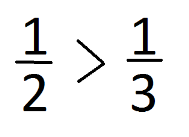
Какие часы показывают большее время: четверть второго или полвторого?
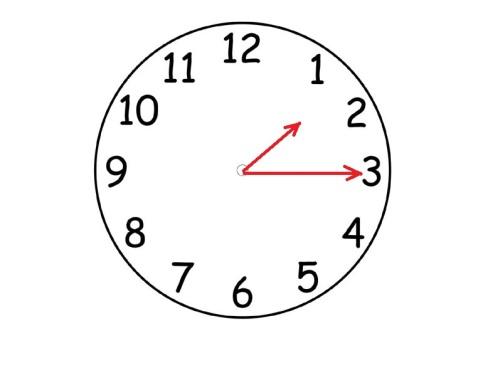
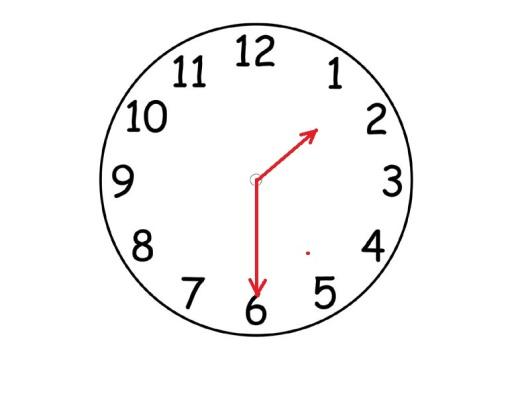
Запишите это в виде неравенства дробей.
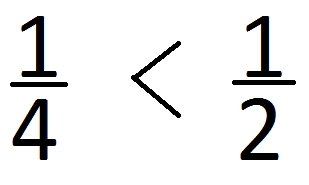
Обратите внимание на числители и знаменатели дробей: что из них является одинаковым, а что различным? Таким образом, мы приступили к сравнению дробей с одинаковыми числителями.
Давайте посмотрим на записанные неравенства и попытаемся понять, по какому правилу можно сравнить дроби, у которых одинаковые числители. Попытайтесь сформулировать это правило.
Изложение нового материала .
А теперь предлагаю вашему вниманию видеоролик, который покажет вам, верно ли вы сформулировали правило.
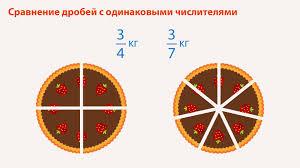
Пришло четверо гостей, и торт разделили на 4 части. Видите, какой кусок достался каждому гостю?
А теперь гостей пришло больше, например 7, тогда торт разрезали на 7 частей. И части получились более мелкие.
Формулируем правило сравнения дробей с одинаковыми числителями:

Какие слова здесь следует выделить, как главные?
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
В этом важное отличие от правила сравнения дробей с одинаковыми знаменателями.
Немного философии .

Знаете ли вы, что Лев Николаевич Толстой был не только писателем, но еще и вел педагогическую деятельность? У него была своя школа в Ясной Поляне, где он преподавал также и математику. Им был написан учебник "Арифметика" в двух частях с указаниями для учителя. «Арифметика» Толстого резко отличалась по своему содержанию не только от учебников арифметики своего времени, но и от учебников арифметики последующих десятилетий. Он говорил: "Математика имеет задачей не обучение счислению, но обучение приёмам человеческой мысли при исчислении".
И вот как он воплотил эту идею как раз в нашей теме. (Слайд). Как вы понимаете смысл этих слов?
Первоначальное закрепление .
Поставьте знаки сравнения, руководствуясь правилом сравнения дробей с одинаковыми числителями.

Ответы:

Тренировочное закрепление .
Расположите эти дроби в порядке возрастания (интерактивное задание):
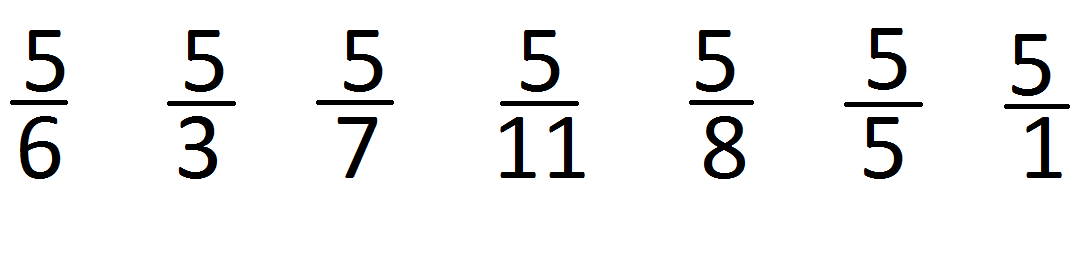
Что значит расположить дроби в порядке возрастания? – Это значит расположить их по порядку от самой меньшей к самой большей.
Какая дробь, согласно правилу сравнения дробей с одинаковыми числителями, будет наименьшей? – Та, у которой знаменатель наибольший. За ней – та, у которой знаменатель следующий по убыванию величины и так далее до дроби с самым меньшим знаменателем.
Ответы:
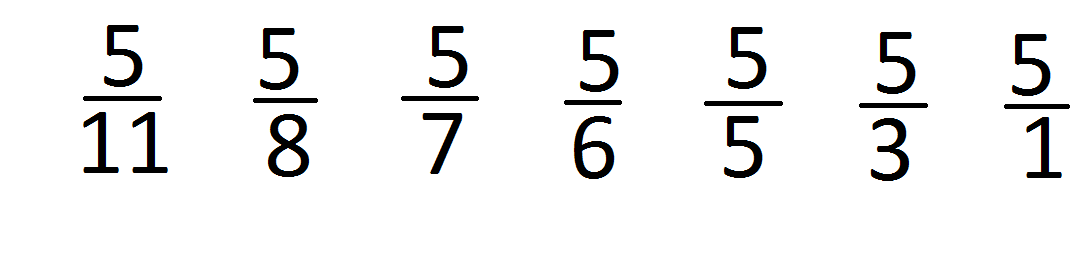
Подберите такие знаменатели, чтобы дроби располагались в порядке убывания:
Что значит расположить дроби в порядке убывания? – Это значит расположить их по порядку от самой большей к самой меньшей.
Какая дробь, согласно правилу сравнения дробей с одинаковыми числителями, будет наибольшей? – Та, у которой знаменатель наименьший. За ней – та, у которой знаменатель следующий по величине и так далее до дроби с самым большим знаменателем.
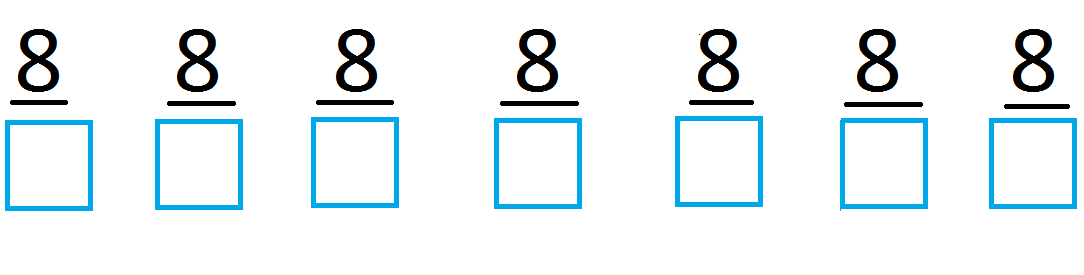
Значит, для решения надо расставить произвольные знаменатели (исключая нуль), расположив их в порядке возрастания.
Например:
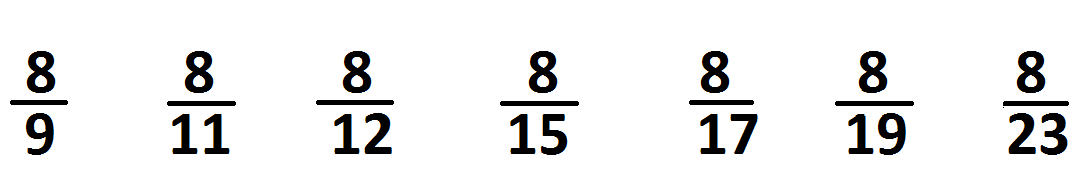
Решение: для этого в знаменателе ставим произвольные числа, расположенные в порядке возрастания. (Нуль в знаменателе исключен, поскольку операция деления на нуль не определена).
Дроби в словах.
Какие слова «спрятались» в этих словах? Расположите их по порядку от самой маленькой к самой большей.
Вот какие дроби "спрятались" в этих словах. В словах "треть" и "четверть" мы слышим части "третья" "четвертая". Со словом «половина» рассуждаем по-другому. На сколько частей надо поделить целое, чтобы получить половину? - На две. Значит, в знаменателе 2. Сколько из них возьмем? - Одну. Отсюда получаем дробь: одна вторая. А слово "полтора" просто надо запомнить - это один с половиной.
И вот как мы теперь запишем их по возрастанию:
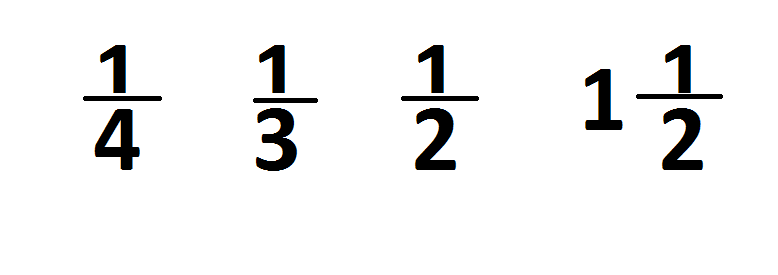
Тематическая физкультминутка.
Я буду называть цепочку из дробей.
Если следующая дробь оказывается больше предыдущей, вы принимаете положение стоя, если меньше – сидя.

Цепочка дробей и правильная последовательность действий:
8 Задание «музыкальная композиция»

Кому знакомы эти знаки? Это ноты, мы видим, что у каждой из них свой «хвостик». Что он обозначает? – Разную длительность звучания.
Чтобы записать мелодию с помощью нот, главное, что требуется, это обозначить для каждой ноты два данных: высоту и ее длительность.
Перед вами (у вас на нотных листочках) – запись некоторой мелодии . В этой записи уже расставлены ноты по высоте, а вот длительность надо отметить вам самим. Для этого под каждой нотой записана дробь, которой она выражена, а вам уже остается приписать правильный «хвостик» к каждой нотке. И тогда вы получите знакомую мелодию, которая вам всем хорошо знакома.

Может, те из вас, кто занимается в музыкальной школе, смогут определить, что это за мелодия? Что ж, проверим.
Звуковой файл с записью мелодии «Два веселых гуся».

Вот какие ноты мы только что записали.

Подведение итогов
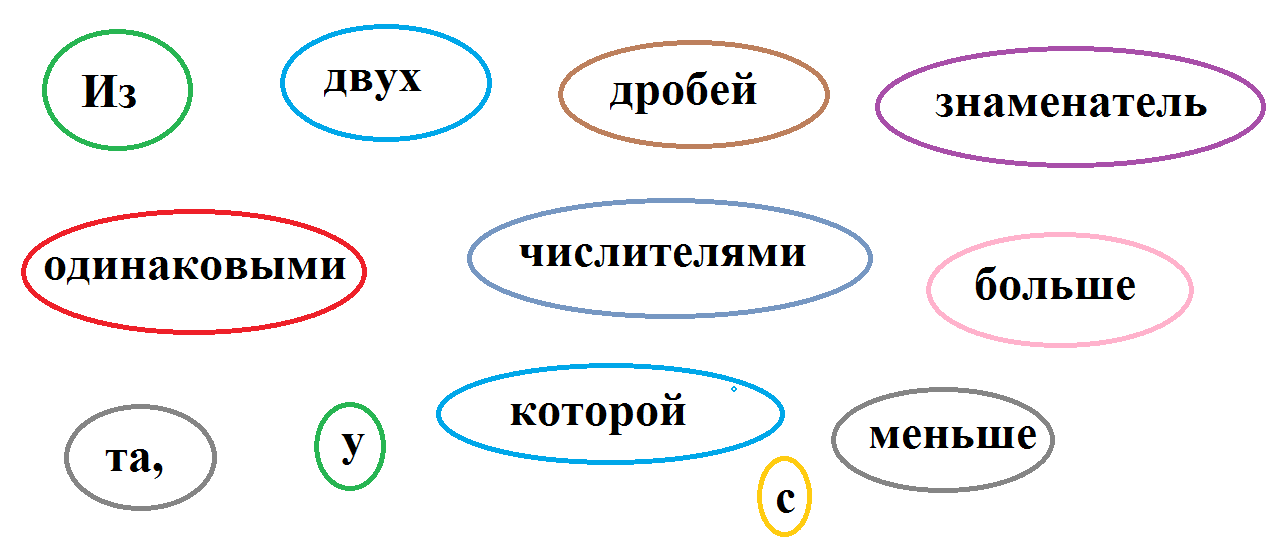
Бусы рассыпались на части. Помогите снова их собрать.
В кружочках написаны слова в разбросанном порядке. Нужно собрать их в правильном порядке так, чтобы получилось правило сравнения дробей с одинаковыми числителями.
Повторяем и проговариваем правило:
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.