Развитие творческих мыслительных способностей невозможно вне проблемных ситуаций, поэтому особое значение в обучении имеют нестандартные задачи. К ним относятся и задачи, содержащие параметр. Математическое содержание этих задач не выходит за пределы программы, тем не менее, их решение, как правило, вызывает у учащихся затруднения.
В применении к параметрическим уравнениям и неравенствам можно выделить следующие исследовательские умения:
1) Умение выражать через параметр условия принадлежности данного параметрического уравнения к тому или иному классу уравнений;
2) Умение определять вид уравнения и указывать вид коэффициентов в зависимости от параметров;
3) Умение выражать через параметры, условия наличия решений параметрического уравнения;
4) В случае наличия корней (решений) уметь выражать условия наличия того или иного количества корней (решений);
5) Умение выражать через параметры сами корни параметрические уравнения (решения неравенства).
Развивающий характер уравнений и неравенств с параметрами определяется их способностью реализовывать многие виды мыслительной деятельности учащихся:
Выработка определенных алгоритмов мышления;
Умение определить наличие и количество корней (в уравнении, системе);
Решение семейств уравнений, являющихся следствием данного;
Выражение одной переменной через другую;
Нахождение области определения уравнения;
Повторение большого объема формул при решении;
Знание соответствующих методов решения;
Широкое применение словесной и графической аргументации;
Развитие графической культуры учащихся.
С чего же начинать обучение решению уравнений с параметрами? Конечно, с азов.
Решить уравнение – значит указать, при каких значениях параметров существуют решения, и каковы они, то есть, исследовать его относительно параметра.
Множество значений параметра разбивают на подмножества, границами которых служат те значения параметра, в которых, или при переходе через которые, происходит качественное изменение уравнения. Такие значения параметра называют «особыми» или контрольными.
Линейные уравнения, содержащие параметр.
Алгоритм решения таких уравнений:
Найти ОДЗ
Решить уравнение относительно х
Определить контрольные значения параметра
Проверить, нет ли таких значений параметра, при которых значение х было бы равно числу, исключенному из ОДЗ
ПРИМЕР № 1.
Решить уравнение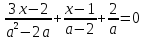
ОДЗ: а2 – 2а ≠ 0 а ≠ 0, а ≠ 2
при а = 0, а = 2 решений нет
приа ≠ 0, а ≠ 2
3х – 2 + ах – а + 2а – 4 = 0
(3 + а)∙х = 6 – а
контрольное значение 3 + а = 0 а = – 3 0∙х = 6 нет решений
а ≠ –3 х = 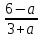
Ответ: при а = 0, а = 2, а = – 3 нет решений
при а ≠ 0, а ≠ 2, а ≠ – 3 х = 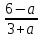
ПРИМЕР № 2.
Решить уравнение 
ОДЗ: х ≠ –1, х ≠ 2
bx – 5x – 2b + 10 – 7x –3bx –7 -3b = 2bx – 5
4bx – 12x = – 8 +5b
4(b + 3)∙x = 8 – 5b
b = – 3 0∙x = 23 нет решений
b ≠ – 3 x = 
Найдём те значения параметра b, при которых х = – 1
 = –1
= –1
– 8 +5b = 4b + 12
b = 20
Найдём те значения параметра b, при которых х = 2
 = 2
= 2
8 + 5b = 8b + 24
13b = – 16
b = 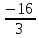
Ответ: при b = – 3, b = 20, b = 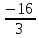 нет решений
нет решений
при b≠ – 3, b≠ 20, b≠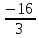 x =
x = 
Квадратные уравнения, содержащие параметр.
Для нахождения контрольных значений параметра при решении квадратных уравнений часто пользуются следующими фактами:
Коэффициент при х2 не должен быть равен нулю;
Значения параметра, при которых дискриминант уравнения D равен нулю, относят к контрольным, так как, если дискриминант обращается в нуль при некотором значении параметра и при переходе через эту точку меняется знак, то при переходе через эту точку меняется число действительных корней квадратного уравнения.
ПРИМЕР № 2.

ОДЗ: x 2, b – 1
при b = – 1 нет решений
при b – 1
x2 – 2x + 2bx + 2x – 3b + 4 =0
x2 + 2bx – 3b + 4 =0
Всё зависит от дискриминанта, найдём его и рассмотрим все случаи.
D = b2 – 4 + 3b = b2 + 3b – 4 = (b + 4)(b – 1)
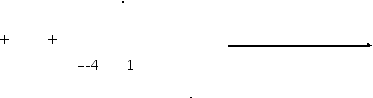
при – 4нет решений
при b b 1
x1 = b +  , x2 = b –
, x2 = b – 
при b = – 4
x2 – 8x + 4 + 12 = 0
x2 – 8x +16 = 0
(x – 4)2 = 0
x = 4
при b = 1
x2 + 2x + 4 – 3 = 0
x2 + 2x + 1 = 0
(x + 1)2 = 0
x= – 1
Найдём те значения параметра b, при которых х = 2.
4 + 4b – 3b + 4 = 0
b = – 8
x2 – 16x + 4 + 24 = 0
x2 – 16x + 28 = 0
x1 = 14, x2 = 2
Ответ: при – 4b
при b = – 8 x = 14
при b = – 4 x = 4
при b = 1 x= – 1
при b b 1
x1 = b +  , x2 = b –
, x2 = b – 
ПРИМЕР № 4.
При каких значениях параметра а найдутся такие значения х, что числа 2х – а; –2-х-1; 4х +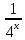 , взятые в указанном порядке образуют арифметическую прогрессию.
, взятые в указанном порядке образуют арифметическую прогрессию.
Решение:
Первый член прогрессии а1 = 2х – а; второй член прогрессии а2 = –2-х-1; третий член прогрессии а3 = 4х +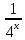 .
.
а2=  ⇒ 2а2 = а1 + а3⇒
⇒ 2а2 = а1 + а3⇒
2(–2-х-1) = 2х – а + 4х +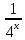
–21∙2-х-1= 2х – а + 4х +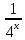
–2-х = 2х – а + 4х +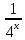
а = (2х + 2-х) + (4х + 4-х) [(2х + 2-х)2 = 4х +2∙2х∙2-х + 4-х = 4х+ 4-х +2]
а = (2х + 2-х) + (2х + 2-х)2 – 2
Введём новую переменную, пусть t = 2х + 2-х, рассмотрим данную функцию и найдём её экстремумы:
 = 2х– 2-х = 0
= 2х– 2-х = 0
2x–  = 0
= 0
22х – 1 = 0
22х = 1
22х = 20
2х = 0
х = 0
y(0) = 20 + 20 = 2 ⇒t 2.
2.
а = t2 + t – 2
t2 + t – (2 – a) = 0
t1,2=  , так как t
, так как t 2⇒t =
2⇒t =  ⇒
⇒
 2
2



 ⇒4а+9
⇒4а+9 ⇒4а
⇒4а ⇒ а
⇒ а 4.
4.
Ответ: при а .
.







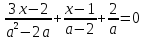
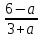


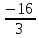

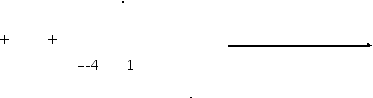
 , x2 = b –
, x2 = b – 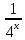 , взятые в указанном порядке образуют арифметическую прогрессию.
, взятые в указанном порядке образуют арифметическую прогрессию. ⇒ 2а2 = а1 + а3⇒
⇒ 2а2 = а1 + а3⇒ = 2х– 2-х = 0
= 2х– 2-х = 0 = 0
= 0









