Стереометрия 10 класс

Часть I

1) Объем конуса равен 56. Через середину высоты параллельно основанию проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найти объем меньшего конуса.

Ответ: 7

2) Сторона основания шестиугольной призмы равна 8, высота равна 12. Найдите площадь боковой поверхности призмы.

Ответ: 576

3) Цилиндр с радиусом основания 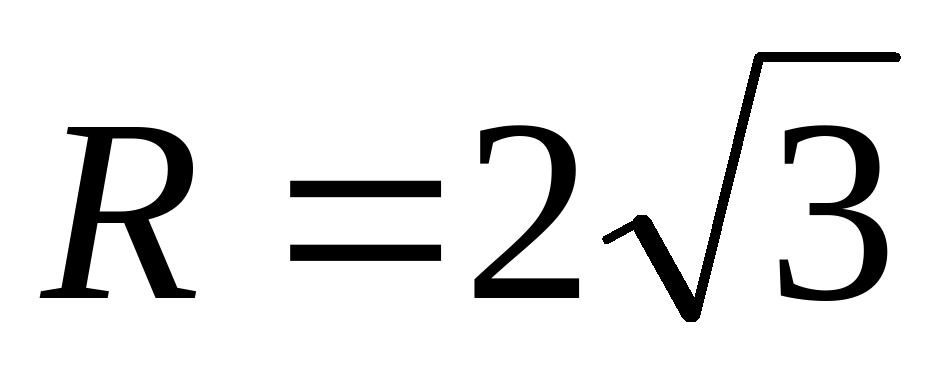вписан в правильную треугольную призму. Найти площадь боковой поверхности призмы, если высота цилиндра 7

Ответ: 84

4) Объем треугольной призмы, отсекаемый от куба плоскостью, проходящей через середины двух ребер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 47. Найдите объем куба.

Ответ: 376

5) Объем параллелепипеда 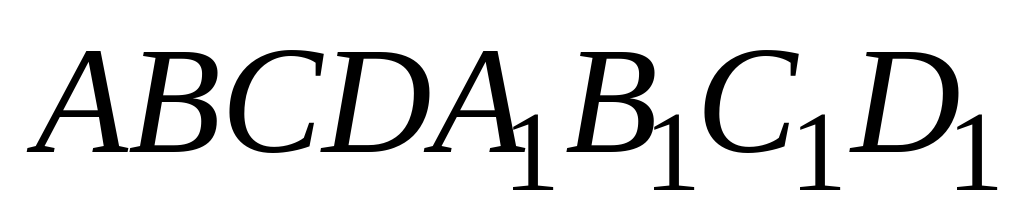равен 3. Найдите объем треугольной пирамиды .

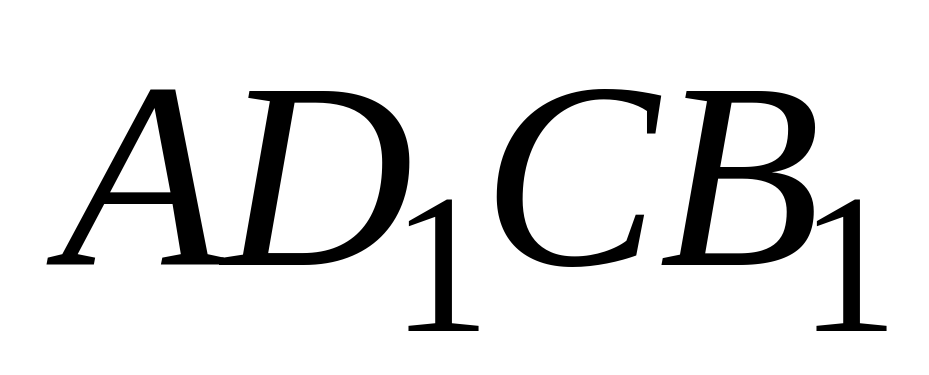Ответ: 1

6) Во сколько раз увеличится объем куба, если его ребра увеличить в раз?

Ответ: 343

Часть II

Задачи для самостоятельного решения. Для зачета достаточно решить 1 задачу из II части

1) В правильной четырёхугольной пирамиде 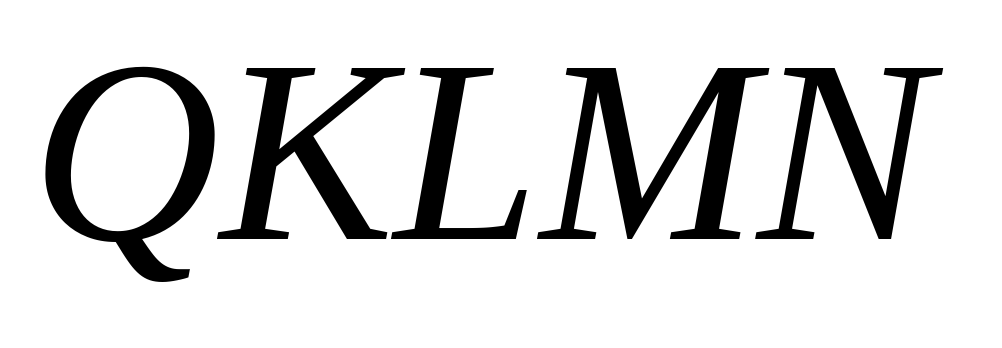сторона основания 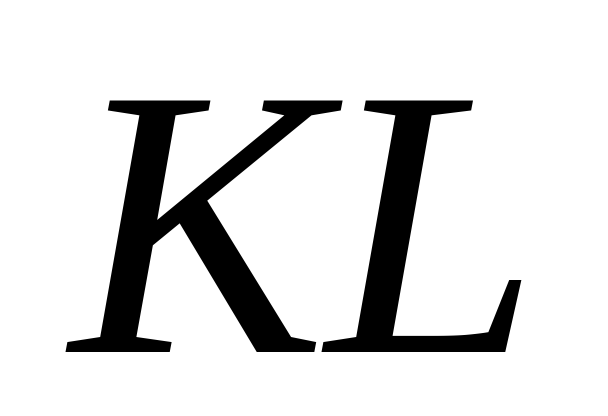равна 8, а боковое ребро 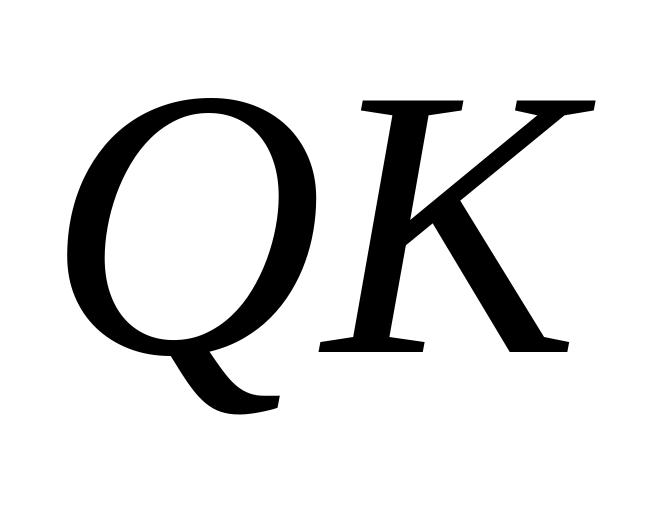равно 10. На ребре 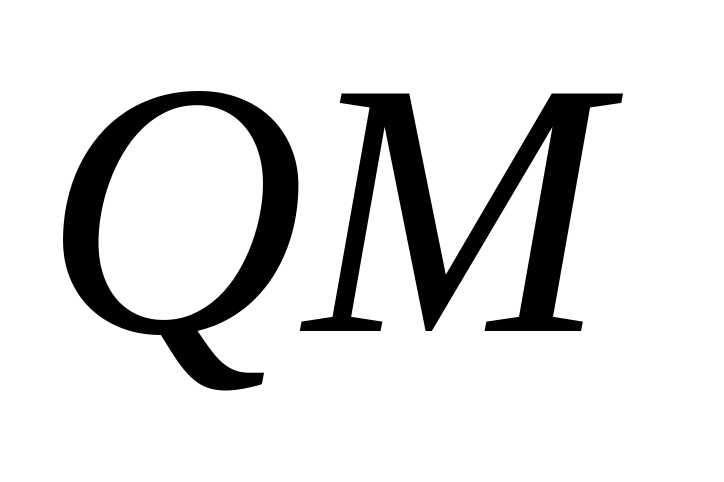взята точка , а на ребре 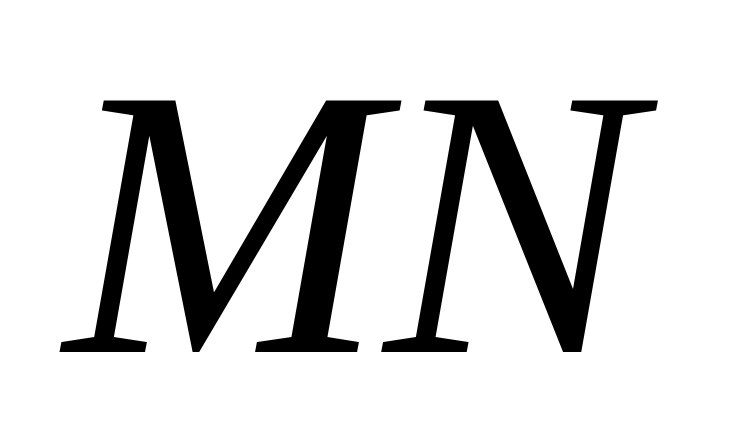- точка 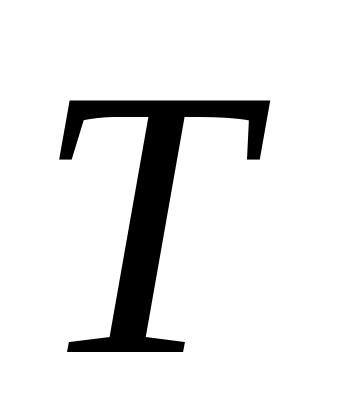, при этом 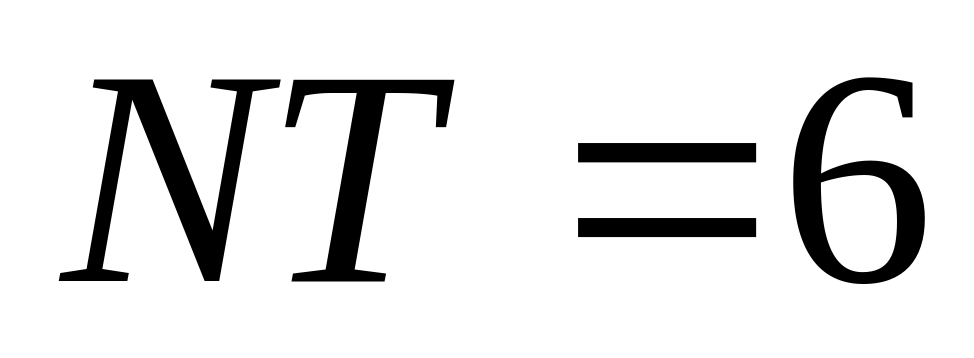и плоскость 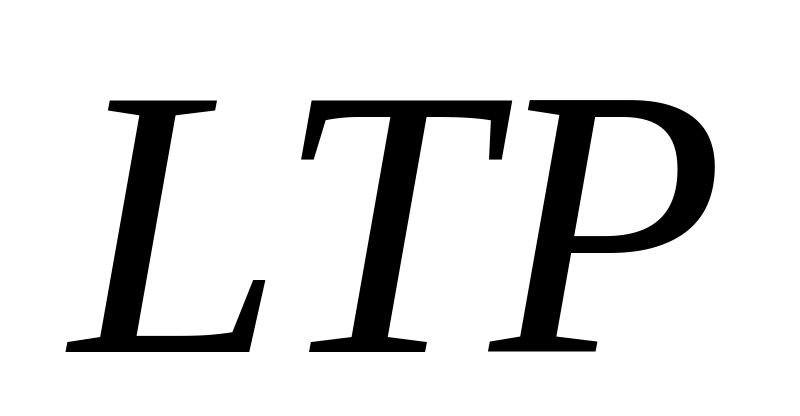перпендикулярна плоскости основания пирамиды.

а ) Докажите, что 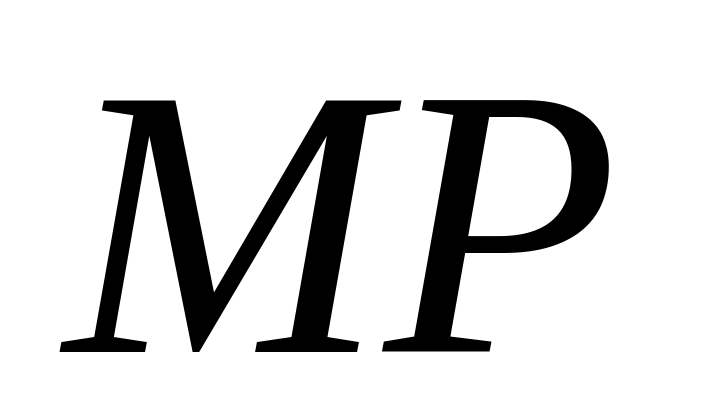равно 4.

б ) Найдите объём многогранника .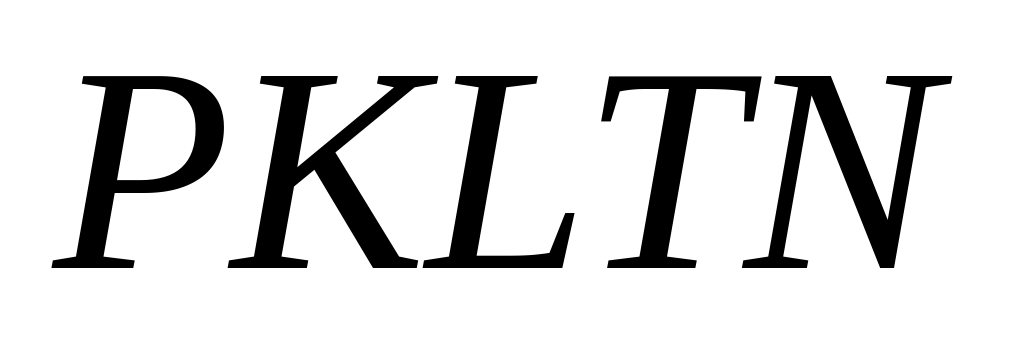

Ответ: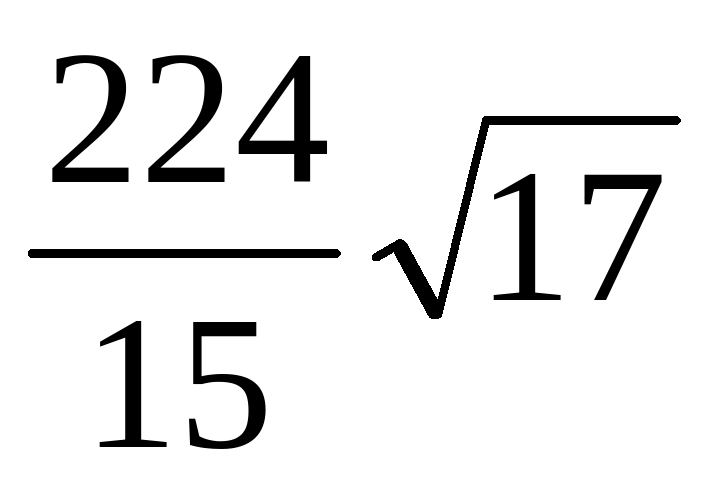

2) В основании пирамиды 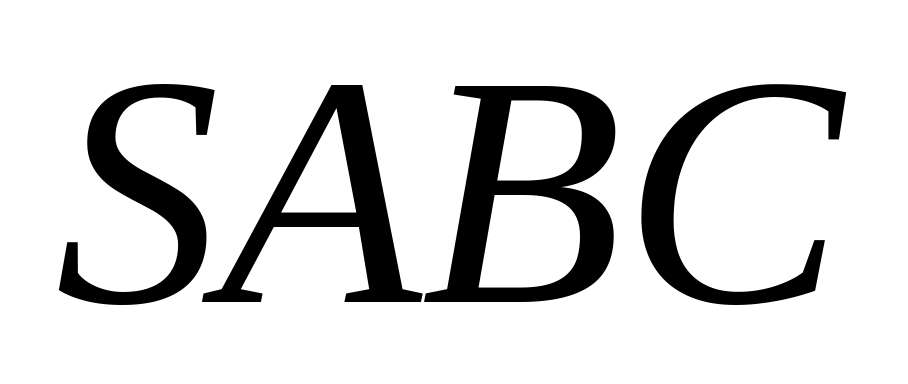лежит прямоугольный треугольник с катетам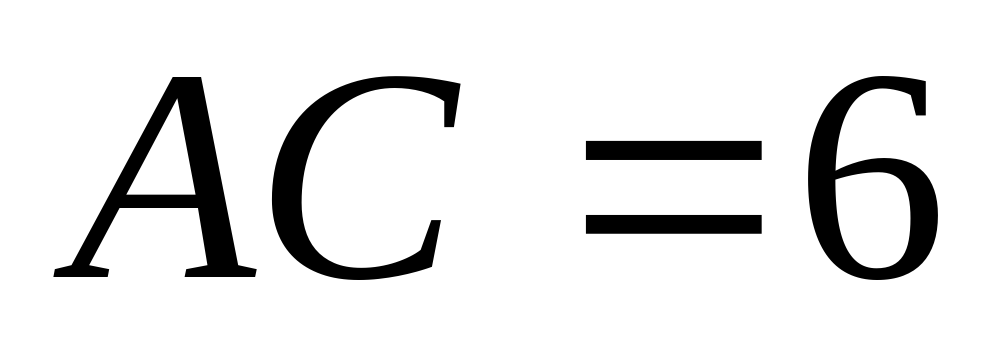и и 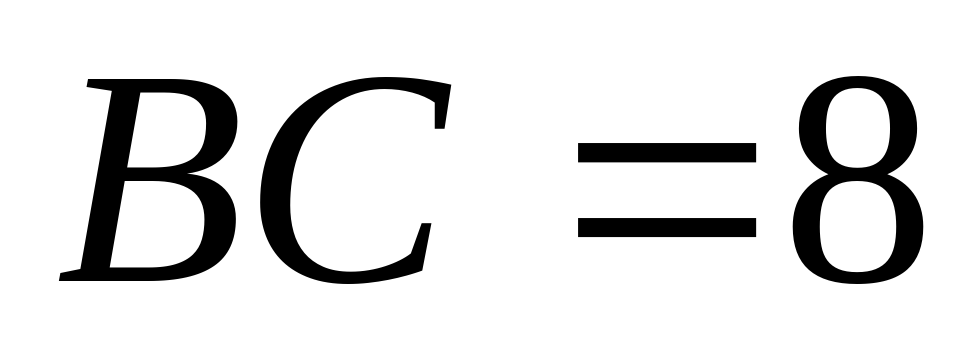. Высота пирамиды равна 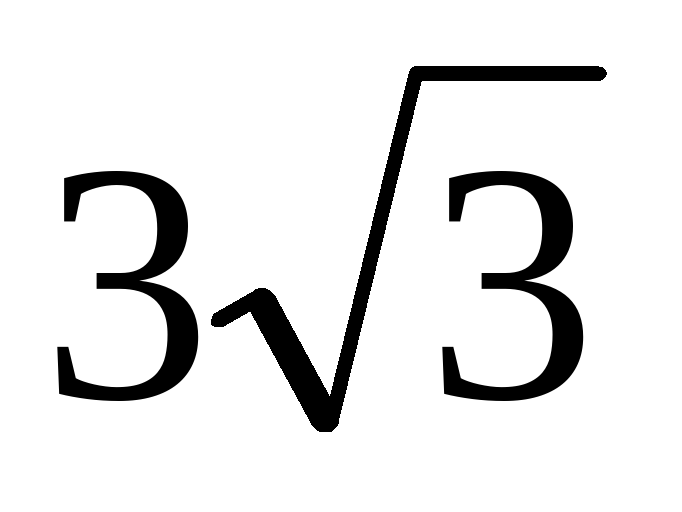, - прямой, а тангенс угла между гранями 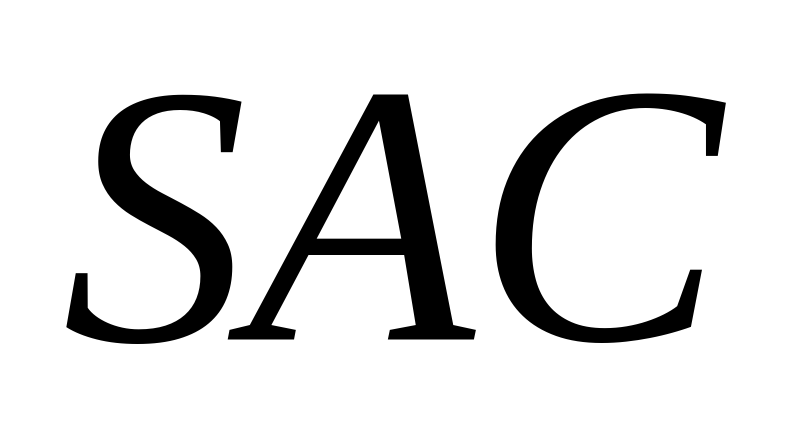и равен ·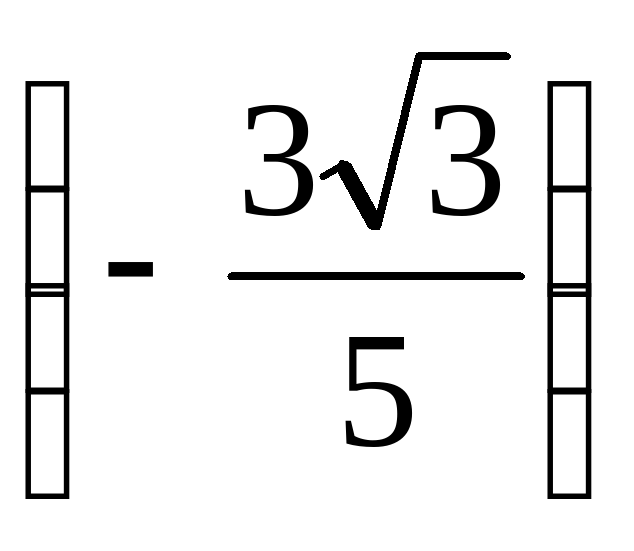

а) Докажите, что угол между плоскостью 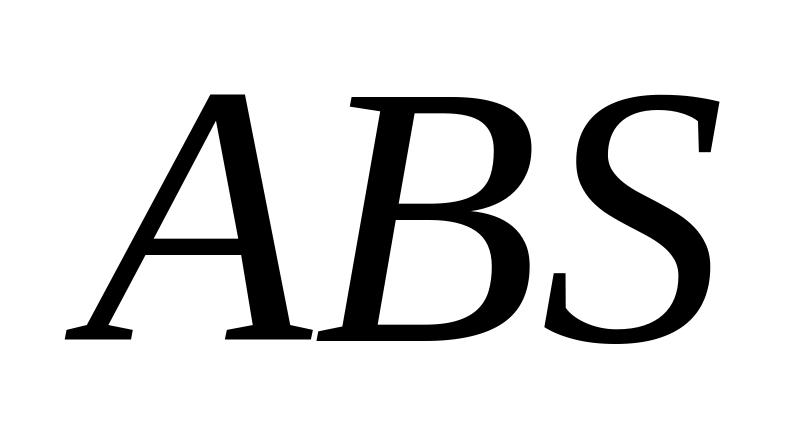и плоскостью основания пирамиды равен .

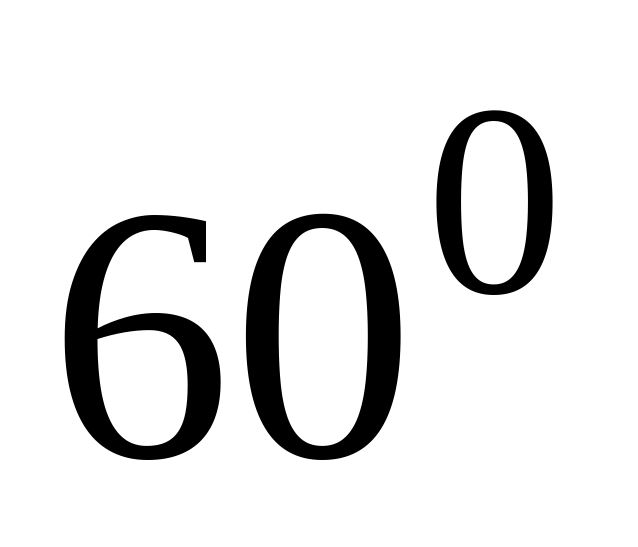б) Найдите площадь грани .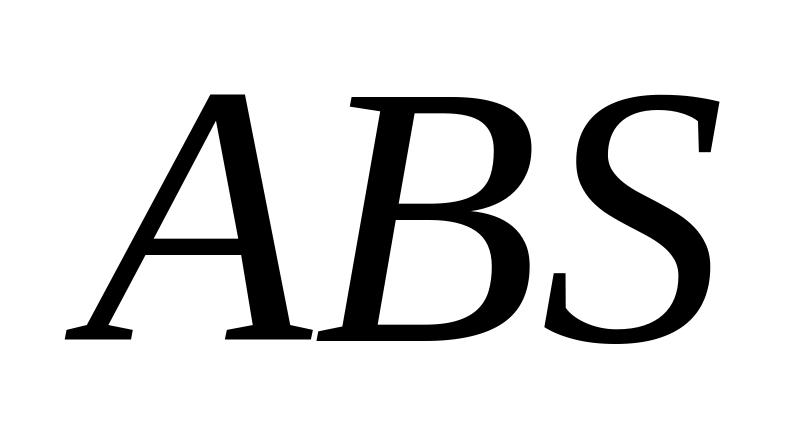

Ответ: 30

3) Дана правильная шестиугольная пирамида 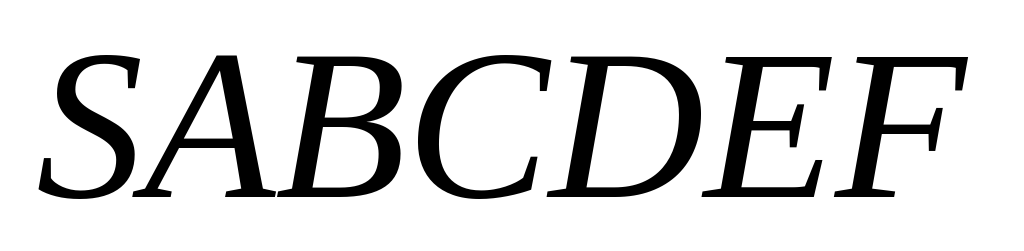с вершиной , стороной основания 12 и боковым ребром 24. На ребре 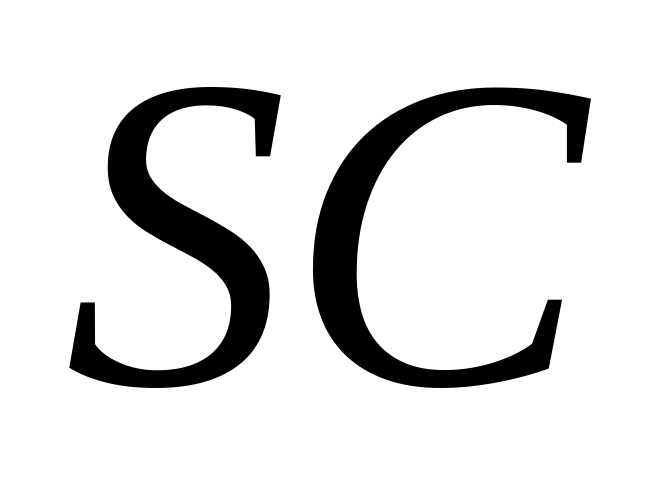выбрали точку , отстоящую от вершины 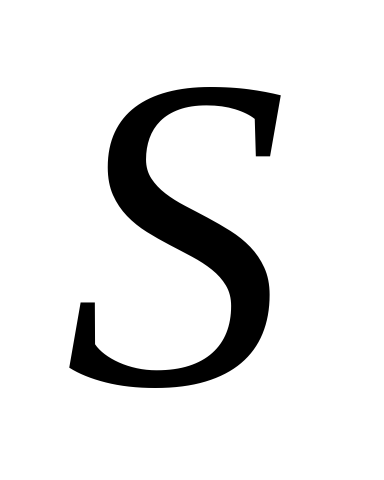на расстояние, равное 6. Через точки и 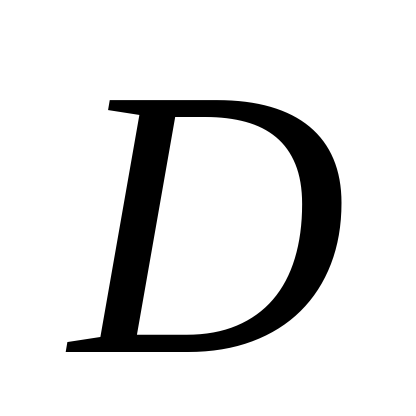перпендикулярно основанию пирамиды проведена плоскость .

а) Докажите, что линия пересечения плоскости с плоскостью основания

пересекает отрезок 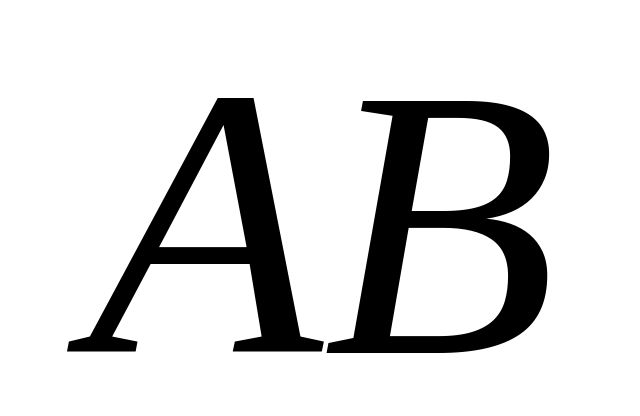в его середине.

б) Найдите объём пирамиды .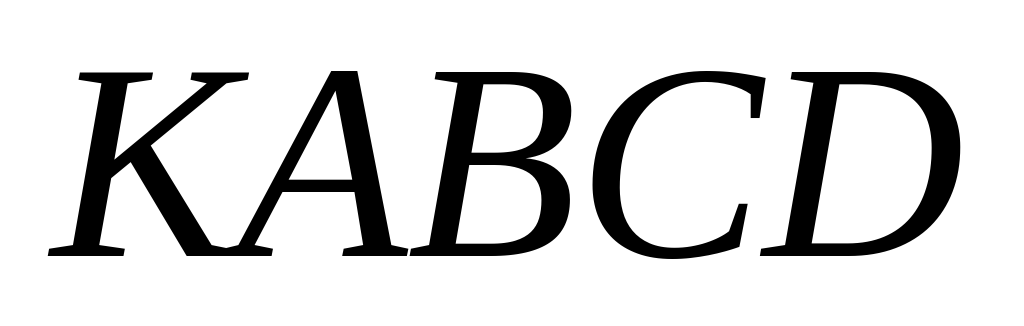

Ответ: 972

4) В основании четырёхугольной пирамиды 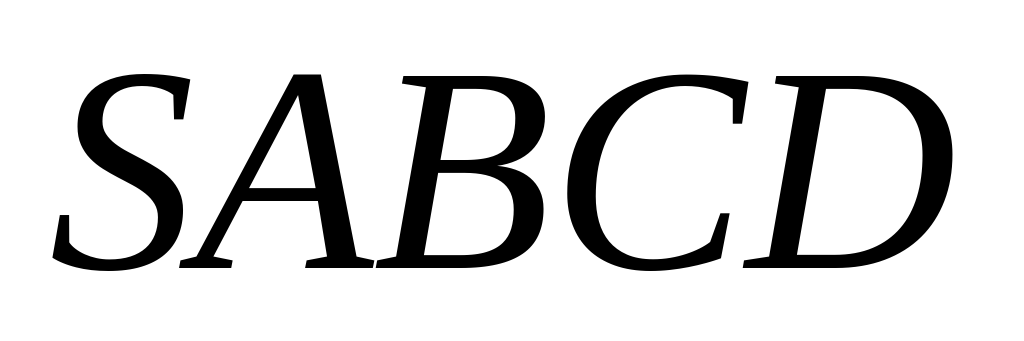лежит квадрат 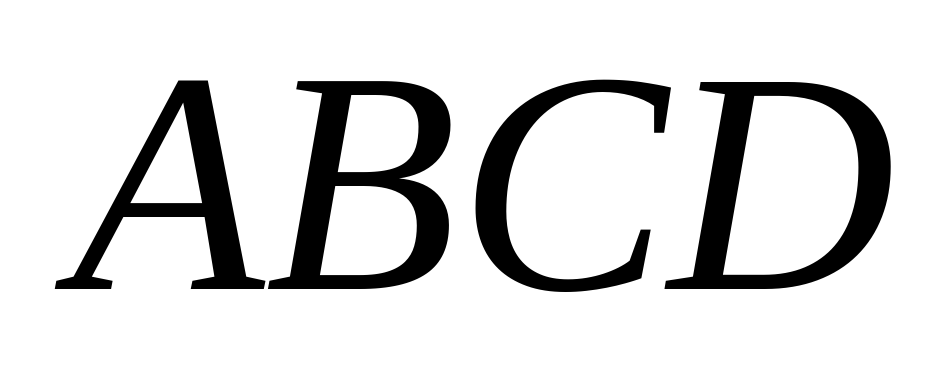. Боковые рёбра пирамиды наклонены к плоскости основания под одним углом. Плоскость проходит через точку 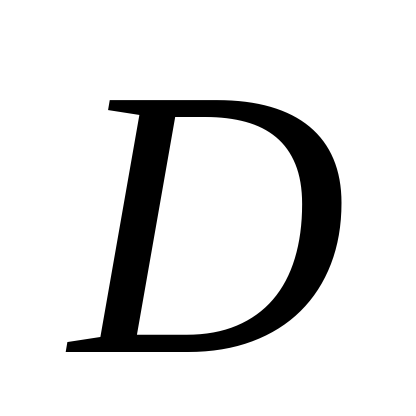и середину высоты пирамиды и параллельна прямой .

а) Докажите, что плоскость делит ребро в отношении , считая от вершины .

б) Найдите синус угла между плоскостью и плоскостью , если угол 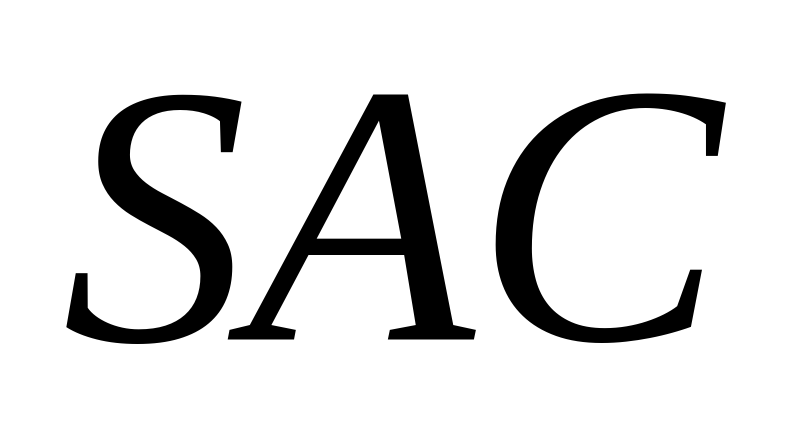равен 30°.

Ответ .

5) В основании четырёхугольной пирамиды 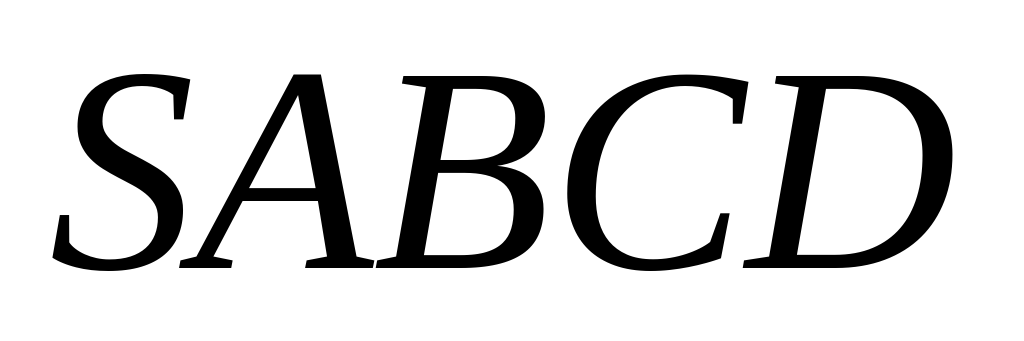лежит квадрат 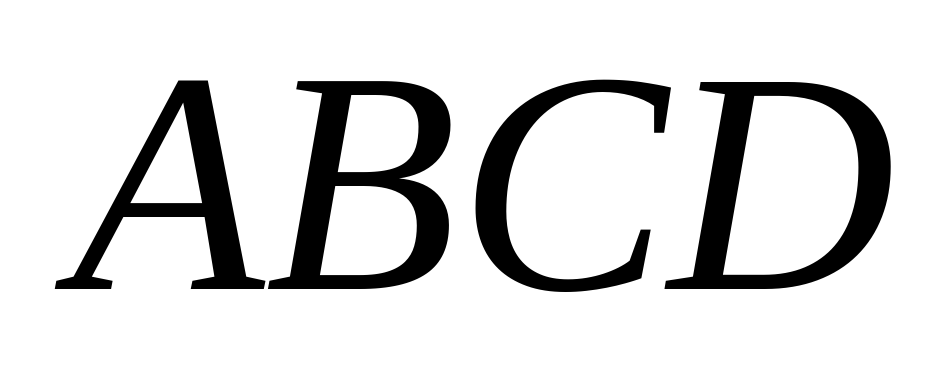. Боковые рёбра пирамиды равны. Плоскость проходит через точку 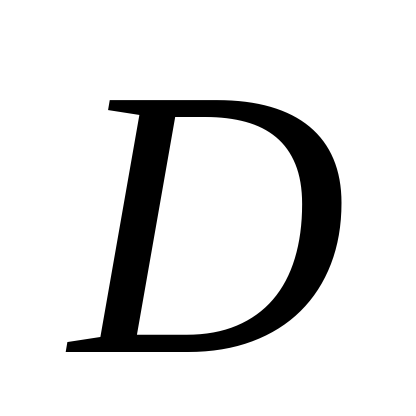, параллельна прямой и делит высоту пирамиды в отношении , считая от вершины .

а) Докажите, что плоскость делит ребро в отношении , считая от вершины .

б) Найдите синус угла между плоскостью и плоскостью , если угол 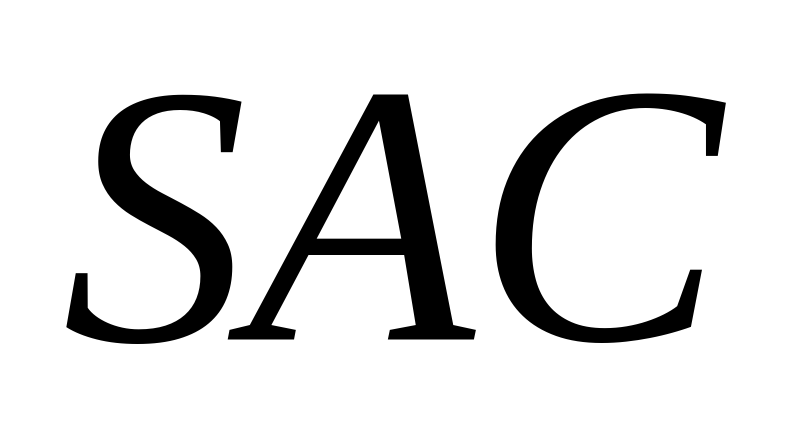равен .

Ответ

6) Сторона основания правильной треугольной пирамиды 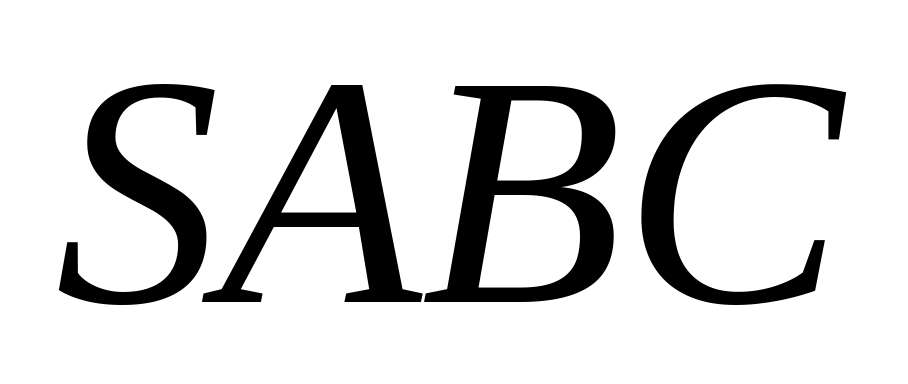равна 10, а боковое ребро равно .· Точка лежит на боковом ребре , а точка на стороне основания 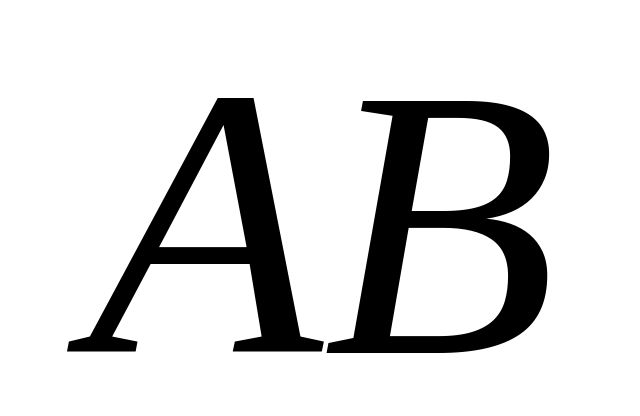, , . Плоскость проходит через точки и и перпендикулярна плоскости .

а ) Докажите, что точка принадлежит плоскости .

б) Найдите площадь сечения пирамиды 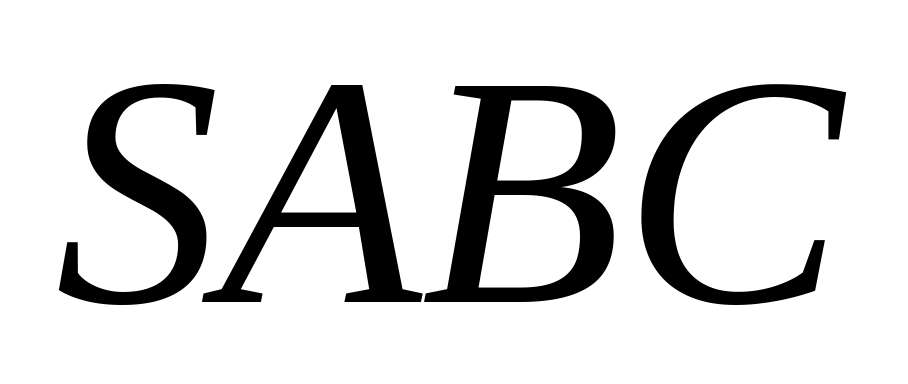плоскостью .

Ответ: