Тема урока: Сумма и разность кубов двух выражений
Тип урока: урок «открытия» новых знаний
Цели урока: - формирование у обучающихся способностей к самостоятельному
доказательству формул на основе метода рефлексивной самоорга-
низации;
- организовать деятельность обучающихся на восприятие,
осмысление и первичное закрепление знаний;
- способствовать формированию умения использовать приемы:
обобщения, сравнения, выделения главного, переноса знаний
в новую ситуацию;
- развитие познавательного интереса к предмету;
- формирование эмоционально-положительного настроя у
обучающихся путем создания доброжелательной деловой рабочей обстановки;;
- развитие рефлексивных умений через проведение анализа резуль-
татов урока и самоанализа собственных достижений;
- воспитывать умение работать в сотрудничестве в парах и группах.
Задачи урока:
Образовательная: вывести формулы суммы и разности кубов двух выражений; научить применять их при преобразовании выражений;
Развивающая: развитие алгоритмического мышления, памяти, внимательности, развитие культуры речи;
Воспитательная: усиление познавательной мотивации осознанием собственной значимости в образовательном процессе, воспитание самостоятельности.
Используемые педагогические технологии, методы, приемы:
Технология деятельностного обучения.
Методы организации работы: - словесный (беседа)
- проблемно-поисковый
- метод рефлексивной самоорганизации
(деятельностный метод)
ХОД УРОКА
1.Самоопределение к деятельности (2 мин.)
Цели для учителя: создание условий для возникновения у обучающихся внутренней потребности включения в учебную деятельность
Цели для обучающихся: включение в учебную деятельность
Еще Аристотель говорил, что « математика выявляет порядок, симметрию и определенность, а это – важнейшие виды прекрасного».
Действительно, после каждого урока неопределенности, неизвестности у нас становится меньше, а овладевать новыми знаниями – что может быть прекраснее!
Вот и сегодня мы с вами сделаем новое открытие, и это – прекрасно!
Улыбнитесь, нас ждут великие дела!
2. Актуализация теоретических знаний ( 5 мин.)
Цели для учителя: - актуализация изученного, необходимого для построения нового знания;
- активизация соответствующих мыслительных операций и познавательных процессов;
- мотивирование обучающихся к пробному учебному действию и его самостоятельное осуществление
Цели для обучающихся: фиксирование индивидуальных затруднений при выполнении пробного учебного задания
2.1Математический диктант « Верно или нет»
Если перед скобками ставится знак «минус», то знаки членов, заключаемых в скобки, записывают с теми же знаками;
Произведение любых двух многочленов можно представить в виде одночлена;
Буквенный множитель одночлена, записанного в стандартном виде, называется коэффициентом одночлена;
Если левая и правая часть равенства тождественно равны одному и тому же выражению, то исходное равенство – тождество;
При умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого многочлена;
Алгебраическая сумма нескольких одночленов является одночленом;
Если перед скобками ставится знак «плюс», то члены, которые заключают в скобки, записываются с теми же знаками.
2.2 Правильно прочитай алгебраическое выражение с переменными
Демонстрируются карточки с алгебраическими выражениями, а уч-ся называют выражения
| КВАДРАТ РАЗНОСТИ | (a - b)2 |
| КВАДРАТ СУММЫ | (a + b)2 |
| РАЗНОСТЬ КВАДРАТОВ | a2 – b2 |
| УДВОЕННОЕ ПРОИЗВЕДЕНИЕ | 2ab |
| ПОЛНЫЙ КВАДРАТ | a2 2ab + b2 |
| Неполный квадрат | a2 ab + b2 |
Подсказка: трехчлен, который можно представить в виде квадрата двучлена, называют полным квадратом
Осуществляем самопроверку по выведенным ответам (нет – 0, да -1):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Нет | нет | нет | Да | да | нет | да |
Открытие нового знания (11-13 мин.)
Цели для обучающегося: - выбор способа решения задания;
- выдвижение гипотезы;
- формулировка новых правил
Задание: «Подумай и сделай открытие»
Древние мудрецы считали: «Величие человека – в его способности мыслить»
Обучающиеся разделяются на группы по рядам. Даю задание:
Пусть даны произведения двух выражений:
(х + y)(x2 - xy + y2) для 1 ряда
(х - y)(x2 + xy + y2) для 2 ряда
(a - 3)(a2 – 3a + 9) для 3 ряда
Умножьте двучлен на трехчлен (подсказка: при умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого многочлена), приведите подобные (подсказка: подобные – слагаемые с одинаковой буквенной частью).
Проанализируйте полученные результаты (как прочитать выражение, полученное справа от знака равенства? – сумма кубов, разность кубов, многочлен). Почему третье выражение не получилось представить в виде разности кубов?
В 7 классе мы изучаем пять формул сокращенного умножения (см. на форзаце учебника). Существует ли формула суммы квадратов?
Сформулируйте правило нахождения суммы (разности) кубов двух выражений
Сделайте вывод:
(a + b)(a2 – ab +b2)=
(a - b)(a2 +ab +b2)=
Обратите внимание: Трехчлен вида (a2 – ab +b2) или (a2 – ab +b2) называют неполным квадратом разности или суммы (Как вы думаете почему?). стр 117 в учебнике
( Идет обсуждение в группах. Далее каждая группа предлагает свою гипотезу, проходит обсуждение, делается вывод)
Первичное закрепление (7 мин.)
Цели для обучающихся: усвоение нового способа действий.
Задание: 4.1 Разложите на множители:
8a3 + 27b3,
x6-y9,
1+x3,
a3b3 - 1
(проводим подробное решение на доске с проговариванием правил)
Задание 4.2 Представьте в виде многочлена:
(2a-3)(4a2 + 6a + 9);
(1+x)(1+x+x2)
Задание 4.3 Работа в парах. Задание на карточках: разложите на множители
125-b3, a3 + 8, m3n3 + 0,001, 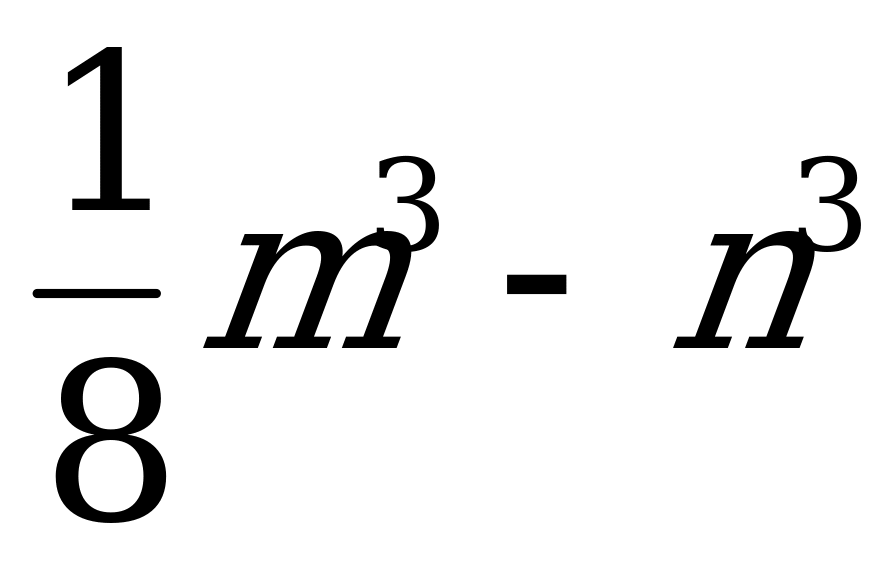
Выполните самопроверку (ответы с решениями демонстрируются на доске)
Самостоятельная работа с самопроверкой ( 4-5 мин.)
Цели для учителя: создание условий для империоризации (переход извне внутрь) нового способа действий
Цели для обучающихся: индивидуальная рефлексия достижения цели.
Задание: попробуйте выполнить по 2 примера самостоятельно:
1 вариант 2 вариант
5 а) разложите на множители: 1-x3, y3 -27
5 б) представьте в виде многочлена выражение: (x-2)(x2 + 2x+4), (2a – 1)(4a2+2a+1)
( выполнившие задание поднимают руку и получают листы самопроверки, где разобраны решения).
Включение в систему знаний и повторение ( 8 мин.)
Цели для учителя: создание условий для включения « открытия» в систему знаний, повторение и закрепление
Цели для обучающихся: включение «открытия» в систему знаний, повторение и закрепление.
Недостаточно просто запомнить формулы и научиться находить сумму и разность кубов двух выражений. Необходимо знать, где эти формулы можно применять.
Сейчас поработаем в группах. Выдается задание группам:
| 6) 1 ряд | Упростить выражение и найдите его значение: (5y-2)(25y2 +10y+4)+8, если y= - 0,2 |
| 6) 2 ряд | Решить уравнение: (3x-1)(9x2 + 3x+1) - 9x(3x2-4)=17 |
| 6) 3 ряд | Докажите, что значение выражения 215 +33 делится нацело на 35 |
Группы выполняют свои задания, далее демонстрируют свои решения классу на доске.
Рефлексия учебной деятельности (2 мин.)
Цели для обучающихся: самооценка результатов деятельности.
Отвечаем на вопросы:
- Достигли ли мы цели урока?
- Каков результат нашей деятельности?
- Сформулируйте правила нахождения суммы и разности кубов двух выражений
- Где используются новые формулы?
- Как бы вы оценили свою деятельность на уроке?
8. Домашнее задание ( по учебнику): Параграф 18, формулы, вопросы, № 671, № 672, № 673, № 678 (7,8), № 680 (1,2)
| (a - b)2 |
| (a + b)2 |
| a2 – b2 |
| 2ab |
| a2 –2ab + b2 |
| a2 +2ab + b2 |
| a2 ab + b2 |
| ЭТАПЫ УРОКА | КАРТА УРОКА 7 класс, Алгебра, (§18, Мерзляк А.Г.) |
| II | 0001101 |
| III | Пусть даны произведения двух выражений: (х + y)(x2 – xy + y2) для 1 ряда (х – y)(x2 + xy + y2) для 2 ряда (a – 3)(a2 – 3a + 9) для 3 ряда 1)Умножьте двучлен на трехчлен (подсказка: при умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого многочлена), приведите подобные (подсказка: подобные – слагаемые с одинаковой буквенной частью). 2) Проанализируйте полученные результаты (как прочитать выражение, полученное справа от знака равенства?). 3) Сформулируйте правило нахождения суммы (разности) кубов двух выражений. 4) Сделайте вывод: (a + b)(a2 – ab +b2)=…; (a - b)(a2 + ab +b2)=… |
| IV | Задание: 4.1 Разложите на множители: 8a3 + 27b3, x6-y9, 1+x3, a3b3 – 1 (проводим подробное решение на доске с проговариванием правил) Задание 4.2 Представьте в виде многочлена: (2a-3)(4a2 + 6a + 9); (1+x)(1+x+x2) (проводим подробное решение на доске с проговариванием правил) Задание 4.3 Работа в парах. Задание на карточках: разложите на множители: 125-b3, a3 + 8, m3n3 + 0,001, 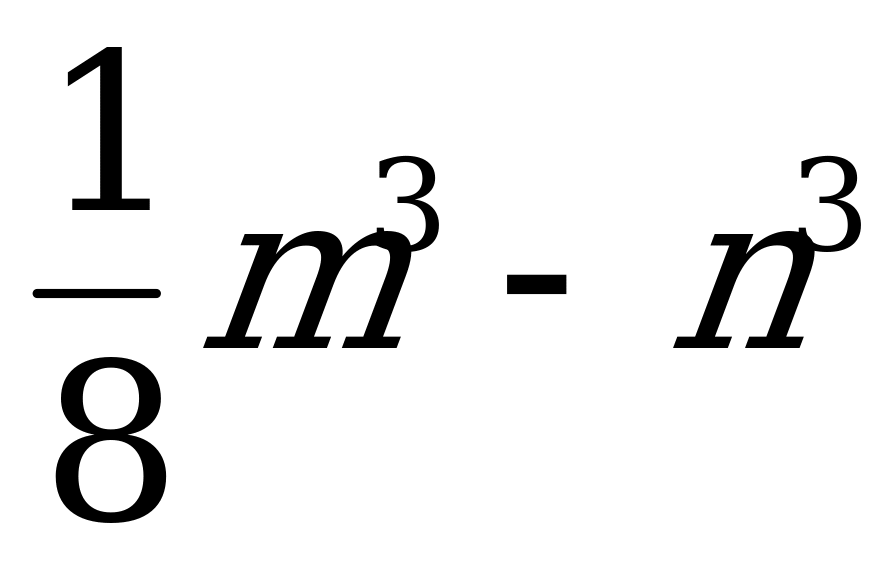 |
| V | Самостоятельная работа (5 МИН) а) разложите на множители: 1 вариант:1-x3, 2 вариант: y3 -27 | б) представьте в виде многочлена выражение: 1 вариант: (x-2)(x2 + 2x+4), 2 вариант: (2a – 1)(4a2+2a+1) ( выполнившие задание поднимают руку и получают листы самопроверки, где разобраны решения). |
| VI | | 1 ряд | Упростить выражение и найдите его значение: (5y-2)(25y2 +10y+4)+8, если y= - 0,2 | | 2 ряд | Решить уравнение: (3x-1)(9x2 + 3x+1) - 9x(3x2-4)=17 | | 3 ряд | Докажите, что значение выражения 215 +33 делится нацело на 35 | Группы выполняют свои задания, далее демонстрируют свои решения классу на доске. |
| VII | Отвечаем на вопросы: - Достигли ли мы цели урока? - Каков результат нашей деятельности? - Сформулируйте правила нахождения суммы и разности кубов двух выражений - Где используются новые формулы? - Как бы вы оценили свою деятельность на уроке? |
| VIII | Параграф 18, формулы, вопросы, № 671, № 672, № 673, № 678 (7,8), № 680 (1,2) |

















