План-конспект открытого урока по теме:
«Сумма углов треугольника».
Ершова Ирина Васильевна учитель математики
Предмет: геометрия.
Класс: 7.
Тема: сумма углов треугольника
Тип урока: изложение нового материала.
Цели урока:
Образовательная: сформировать представление о константной характеристике суммы углов треугольника, добиться усвоения текста теоремы и умения решать задачи на непосредственное ее применение;
Воспитательная: воспитывать трудовые навыки, чувство ответственности, эстетическое начало, стимулировать любознательность и творческую деятельность;
Развивающая: развивать общекультурный уровень, учебные навыки устной речи, самостоятельной работы, работы в группах и коллективе, анализа условия задачи, навыки работы с чертежными инструментами, зрительного представления, творческого воображения.
Оборудование и пособия: интерактивная доска, слайды, 3 дорожки: зеленая, желтая, красная, «таинственный» сундук, листы для «таинственного» сундука: с одной стороны – слова теоремы, с другой – изображения углов, бумажный макет треугольника, чертежные принадлежности у каждого учащегося, транспортир, набор рабочих листов для первоначального закрепления – лист1, для группового задания – лист 2 и для прикладной задачи – лист 3,.
Этапы урока.
| 1. Организация начала урока. Целеполагание. |
| 2. Актуализация опорных понятий |
| 3. Изложение нового материала. |
| 4. Первоначальное закрепление. |
| 5. Тренировочное закрепление. |
| 6. Физкультминутка «черчу треугольник» |
| 7. Задача прикладного характера |
| 8. Экскурс в искусство |
| 9. Подведение итогов |
Ход урока.
Целеполагание.
- Перед вами – «таинственный» сундук. Прочитайте, что написано на нем:
« Здесь есть то,
что каждый школьник
должен знать
про треугольник».
Сегодня на уроке вам предстоит узнать, так что же такое про треугольник должен знать каждый. Но вначале вам надо добраться до этого сундука, а ведут к нему 3 дорожки.
Актуализация опорных понятий.
К доске вызываются три желающих. Они распределяются по договоренности на три дорожки. Тот, кто первым пройдет по одной из трех дорожек, получит право открыть этот ящик. Один шаг по дорожке – это ответ на вопрос.
Зеленая дорожка – самая длинная, но самая безопасная: здесь есть возможность двух неправильных ответов (в случае неправильного ответа – все равно переход хода). У желтой дорожки – одна такая возможность, красная дорожка – самая короткая, но здесь ошибаться нельзя: надо правильно ответить на два вопроса.
| шаг | Вопросы для дорожек |
| красная | желтая | зеленая |
| 1 | Как называется треугольник с двумя равными сторонами? /равнобедренный/ | Как называется треугольник с тремя равными сторонами? /равносторонний/ | Что вы знаете об углах при основании равнобедренного треугольника? / углы при основании равнобедренного треугольника равны/. |
| 2 | Как называется угол, величина которого равна 90 градусам? /прямой/ | Как называется угол, величина которого больше 90 градусов? /тупой/
| Как называется угол, величина которого меньше 90 градусов? /острый/ |
| 3 |
| 
Как называются углы 1 и 2 , представленные на данном чертеже? /смежные/ | 
Как называются углы 1 и 2 , представленные на данном чертеже? /вертикальные/ |
| 4 |
|
| Сколько градусов составляет развернутый угол? /180˚/ |
3.Изложение нового материала.
3.1 Подведение к формулировке теоремы.
Выигравший открывает сундучок. В нем – задание, которое ему предстоит выполнить: расположить эти углы в порядке возрастания их градусных мер.
С одной стороны:

На обороте:

В это время класс в парах выполняет задания из рабочего листа 1.

Вы видите треугольник на листе. У каждой пары он свой. Давайте измерим его углы и найдем их сумму, а потом сравним, что получилось у каждого из вас.
Назовите получившуюся сумму углов. Треугольники у всех разные, а суммы углов у них (почти) одинаковые. Какое предположение можно сделать? В науке такое предположение называется гипотезой.
Но всякая гипотеза нуждается в проверке. Проверим правильность сделанного предположения на макете треугольника.
3.2 Формулировка и обоснование теоремы
Задания в группах. На листе бумаги отметьте три произвольные точки. Постройте треугольник, а затем вырежьте его. Далее согните, как указывают стрелки на образце.

Какой угол составляют все три угла треугольника? – Развернутый.
Учащиеся приходят к выводу о том, что все три угла треугольника в сумме составляют развернутый угол, а значит, 180˚.
Теперь это уже не гипотеза, а научный факт – теорема. Только открыли ее еще древние египтяне в 5 веке до н.э. Дадим ей окончательную формулировку. Обратимся к выполненному победителем заданию.
Ученику было дано задание расположить эти углы в порядке возрастания их градусных мер. Учащиеся проговаривают названия каждого из представленных углов. а теперь проверка: если задание выполнено правильно, должен получиться текст теоремы.
Переворачиваем карточки. Знакомимся с текстом и доказательством теоремы.
3.2. Доказательство теоремы о сумме углов треугольника.
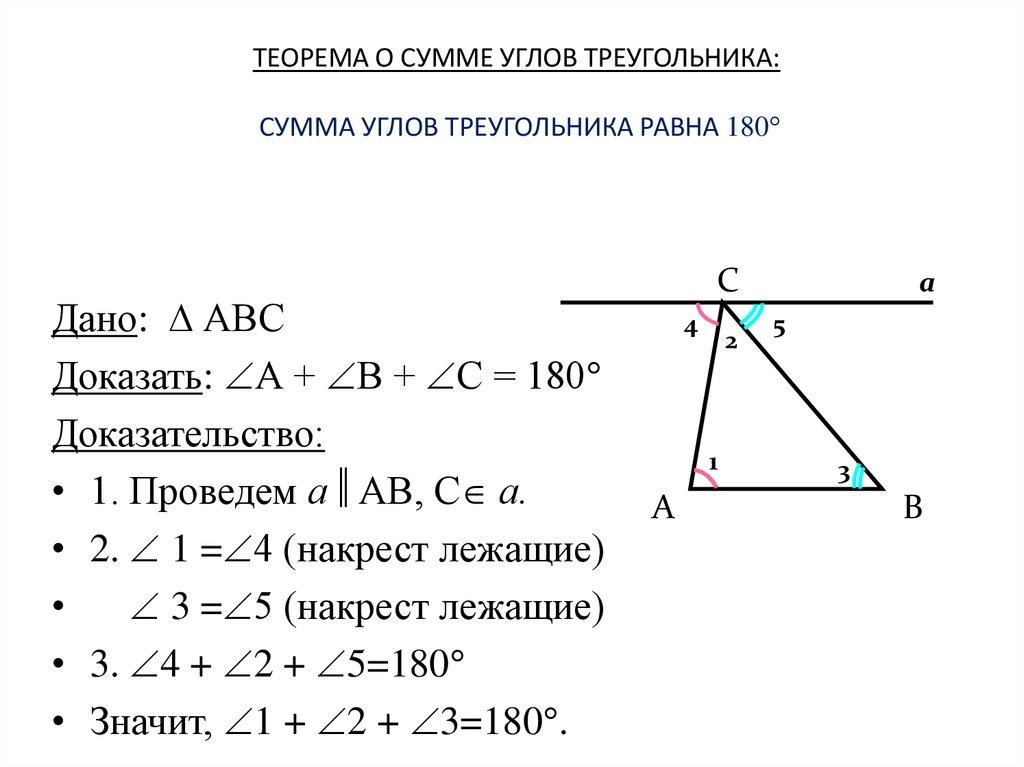
Первоначальное закрепление.
А теперь я предлагаю вам мини-викторину, ответить на вопросы которой нам поможет теорема о сумме углов треугольника. Участвуете вы все. Я задаю вопрос. А вы поднимаете руки, если ответ –«да».
-Верно ли, что можно ли построить треугольник, у которого два тупых угла? /нет, их сумма больше 180˚/
-Верно ли, что можно ли построить треугольник, у которого один из углов тупой, а другой – прямой? /нет, их сумма больше 180˚/
-Верно ли, что можно ли построить треугольник, у которого два прямых угла? /нет, их сумма больше 180˚/
-Верно ли, что если у треугольника равны три стороны, то и все его три угла равны? /да, это следует из попарного равенства углов/
Тренировочное закрепление.
А теперь потренируемся применять полученные знания. У каждого из вас в рабочей папке подготовлен лист 2 и указан номер своей группы. Разделитесь на группы, согласно номеру, и в рабочем листе вам предстоит вычислить значение неизвестного угла, пользуясь теоремой о сумме углов треугольника.

№1 : 45˚ № 2: 60˚

№ 3: 20˚ №4: 80˚
Физкультминутка «Черчу треугольник»
Вы видите, что для выполнения многих математических заданий требуется внимание. Займемся его развитием. Упражнение на координацию движений. Встаньте со своих рабочих мест. Обеими руками чертим в воздухе два треугольника. Теперь задание усложняется: правая рука продолжает чертить треугольник, а левая – круг. А теперь руки меняются ролями!
Задача прикладного содержания.
Перед вами известная всем картина.

Джоконда. Обсудить, что это за картина, как она называется, кто ее автор.
Ее известность проходит сквозь века, и это удивительно, ведь картина не содержит ни захватывающего сюжета, ни помпезности, это всего лишь портрет. Но он очаровывает. А вы знаете, что секрет ее очарования объясняется не только художественными приемами, но и заложенными в ней математическими закономерностями?
Леонардо да Винчи попытался максимально использовать наиболее благоприятную для человеческого глаза пропорцию, открытую скульпторами Древней Греции. А эпоха Возрождения – это и есть возрождение древней греческой культуры.
Он ночами тайно, чтобы не навлечь гнев инквизиции, откапывал свежие захоронения с тем, чтобы изучить строение человеческого тела. Он подтвердил, что строение человека, всех его суставов подчиняется этой пропорции и в восторге назвал ее «золотым сечением». Но о том, что же это за пропорция и чему равно число «золотого сечении», вы узнаете на уроках алгебры. А сейчас мы заговорили об этом, потому что в этой картине есть кое-какой секрет и для нынешней нашей темы.

- Леонардо вписал изображение Джоконды в «золотой» равнобедренный треугольник, т.е. такой, у которого отношение боковой стороны к основанию равно числу «золотого сечения». Ее руки сложены по биссектрисам углов этого треугольника, причем образуются новые «золотые» треугольники.
(По щелчку мыши на изображение накладывается чертеж. Затем изображение плавно растворяется и остается только чертеж, по которому учащиеся работают над решением задачи).
Вопрос: какие углы потребовалось вычислить Леонардо да Винчи, чтобы получить «золотой» треугольник, и под каким углом ему надо было расположить руки Джоконды, чтобы они образовывали «золотые» треугольники? Иными словами, чему равны углы «золотого» треугольника.
По щелчку мыши убирается изображение Джоконды, остается один чертеж. Приготовьте рабочий лист 3. перед вами – «канва» решения. Правильно заполнив пропуски, вы получите решение задачи.

Решение.
Т. к. АВ=ВС, то…………… /углы А=С/
Т. к . АЕ и СМ- биссектрисы, то угол 1…… /= углу 2/
Рассмотрим треугольник АЕС.
Т. к. это равнобедренный треугольник по условию, то…………… /углы Е=С/
Обозначим угол 1=х,
тогда в треугольнике АЕС углы будут выражаться так:
…………………………… /угол 1=х, углы Е=С=2х/
Применяем для этого треугольника теорему о сумме углов треугольника, получаем уравнение:
……………………… /х+2х+2х=180.
Решая его, получаем: х=………. /36˚/
Тогда найдем углы А и С:
………………………… /72˚, 72˚/
Ответ: ………………………… /36˚,72˚,72˚/ – углы «золотого» треугольника.
Экскурс в искусство
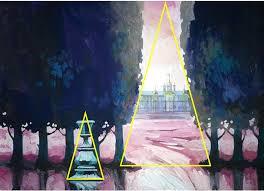
Итак, мы поняли, как получать треугольник «золотого сечения» или, проще, «золотой» треугольник. Вот он.

Пропорции «золотого» треугольника активно используются в архитектуре и живописи.






Подведение итогов.
Что нового вы узнали сегодня на уроке? Ученики проговаривают теорему.
Вернемся к названию темы.
Существует ли подобная теорема для четырехугольника, как вы думаете? Может, суммы углов всех четырехугольников тоже равны между собой? А верно ли это для пятиугольников, шестиугольников и т. д.? Но на этот вопрос я вам не буду сообщать ответ прямо сейчас, об этом вы узнаете на следующих уроках геометрии.
10



































