Свойства биссектрисы и медианы треугольника

• Свойства биссектрисы и медианы треугольника

Автор:

Сидорова А.В.

учитель математики

МБОУ СОШ № 31

г. Мурманска

• Что мы знаем о биссектрисе треугольника из школьного учебника?

• Определение

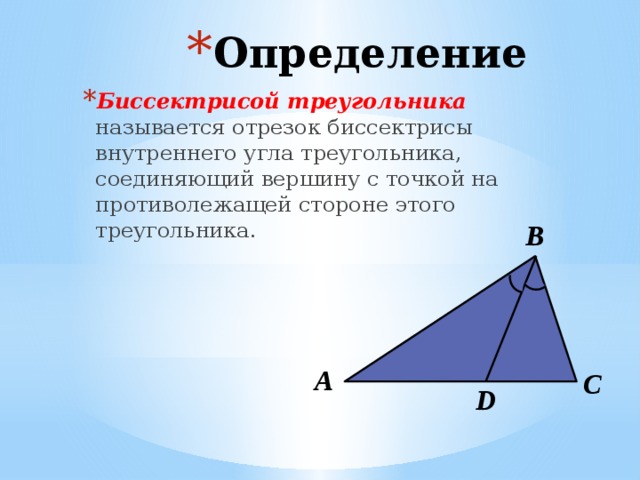
• Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.

В

А

С

D

• Свойства биссектрисы

А

D

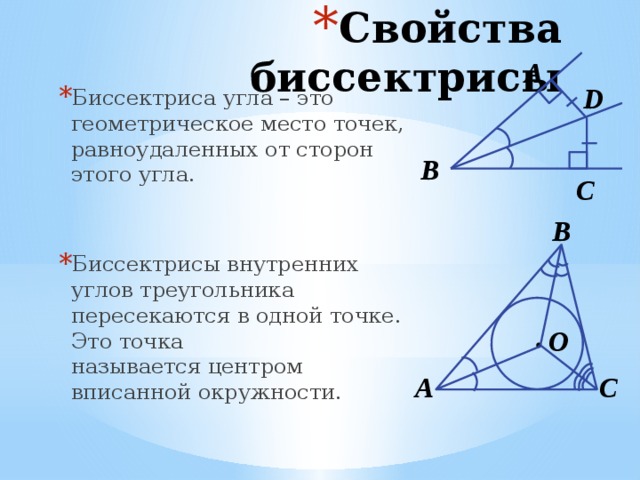
• Биссектриса угла – это геометрическое место точек, равноудаленных от сторон этого угла.

• Биссектрисы внутренних углов треугольника пересекаются в одной точке. Это точка называется центром вписанной окружности.

В

С

В

О

А

С

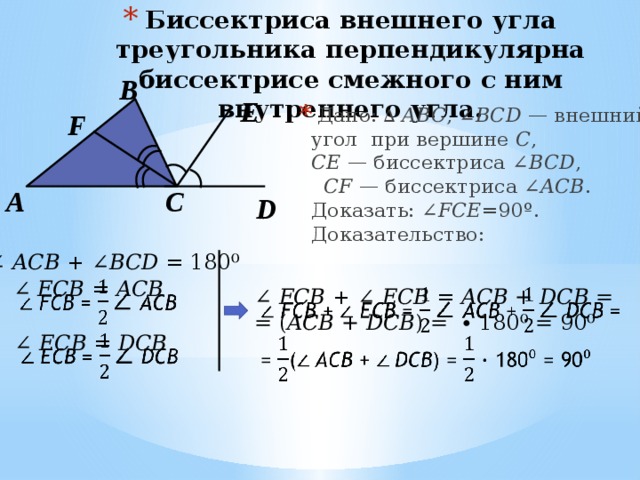
• Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.

В

Е

•   Дано:  ∆ ABC , ∠ BСD — внешний угол при вершине C , CE — биссектриса ∠ BCD , CF — биссектриса ∠ ACB . Доказать: ∠ FCE =90º. Доказательство: 

F

А

С

D

∠ ACB + ∠ BCD = 180⁰

∠ FCB = ACB

∠ FCB + ∠ ECB = ACB + DCB =

= ( ACB + DCB ) = ∙ 180⁰ = 90⁰

∠ ECB = DCB

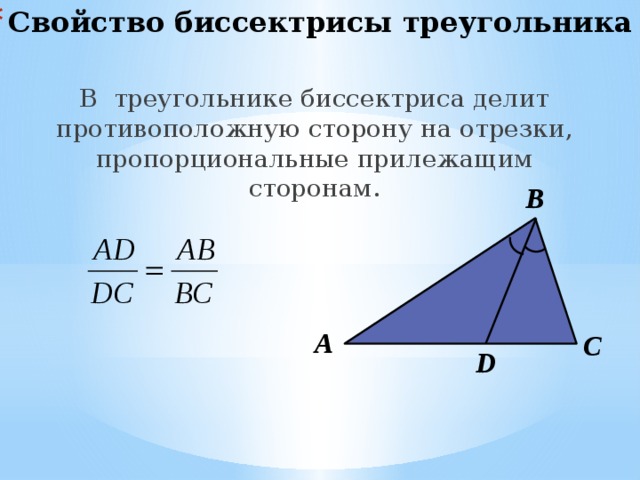
• Свойство биссектрисы треугольника

В треугольнике биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

В

А

С

D

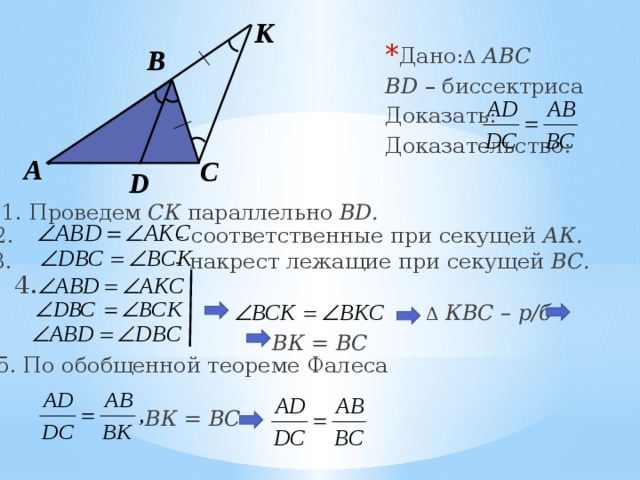
К

• Дано: Δ АВС

BD – биссектриса

Доказать:

Доказательство:

В

А

С

D

1. Проведем СК параллельно BD.

2. - соответственные при секущей АК.

3. - накрест лежащие при секущей ВС.

4.

Δ КВС – р/б

ВК = ВС

5. По обобщенной теореме Фалеса

ВК = ВС

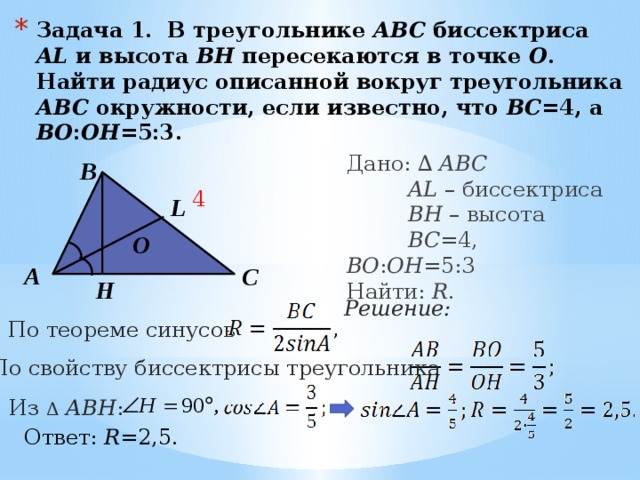
• Задача 1. В треугольнике АВС биссектриса AL и высота ВН пересекаются в точке О . Найти радиус описанной вокруг треугольника АВС окружности, если известно, что ВС =4, а ВО : ОН =5:3.

Дано: ∆ АВС AL – биссектриса ВН – высота ВС =4, BО : ОН =5:3 Найти: R .

В

4

L

О

А

С

Н

Решение:

По теореме синусов

По свойству биссектрисы треугольника

Из Δ АВН :

Ответ: R =2,5.

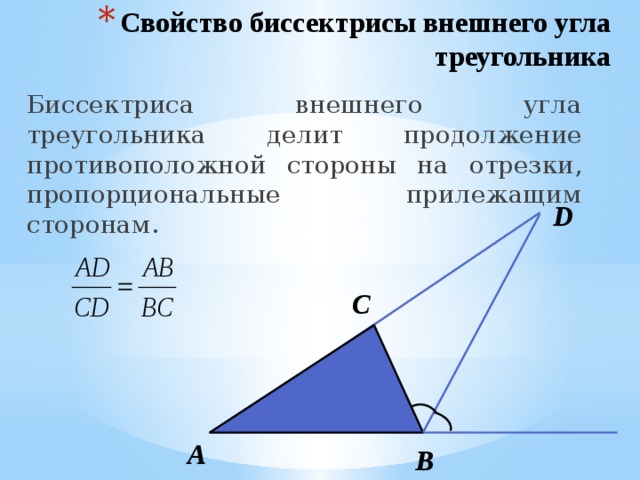
• Свойство биссектрисы внешнего угла треугольника

Биссектриса внешнего угла треугольника делит продолжение противоположной стороны на отрезки, пропорциональные прилежащим сторонам.

D

С

А

В

• Дано: Δ АВС

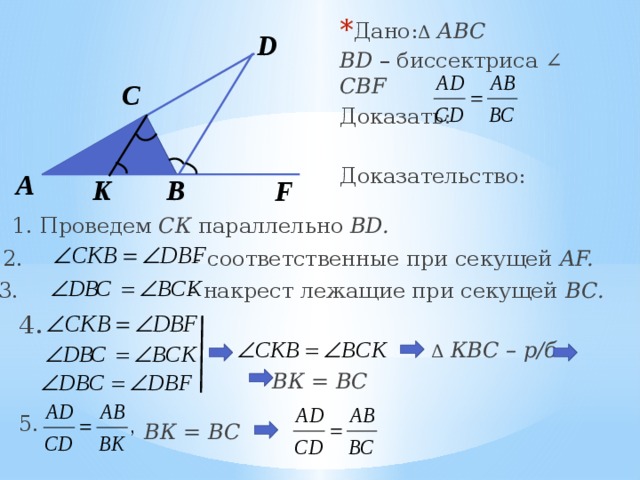
BD – биссектриса ∠ CBF

Доказать:

Доказательство:

D

С

A

K

B

F

1. Проведем СК параллельно BD.

2. - соответственные при секущей AF.

3. - накрест лежащие при секущей ВС.

4.

Δ КВС – р/б

ВК = ВС

5.

ВК = ВС

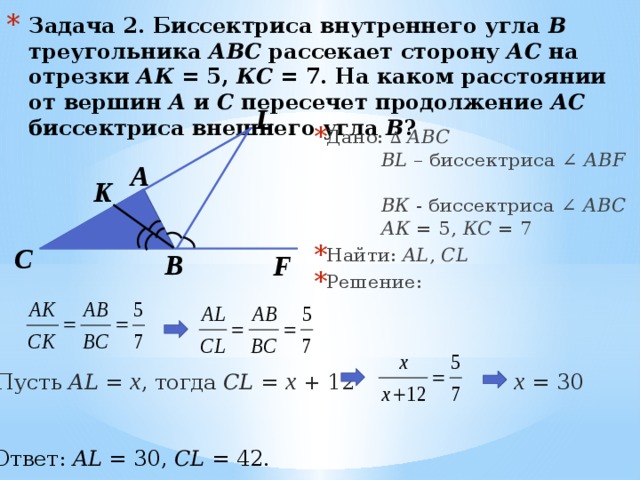
• Задача 2. Биссектриса внутреннего угла В треугольника АВС рассекает сторону АС на отрезки АК = 5, КС = 7. На каком расстоянии от вершин А и С пересечет продолжение АС биссектриса внешнего угла В ?

L

• Дано: ∆ АВС BL – биссектриса ∠ АBF ВК - биссектриса ∠ АBС АК = 5, КС = 7
• Найти: AL , CL
• Решение:

A

K

C

B

F

х = 30

Пусть AL = х , тогда CL = x + 12

Ответ: AL = 30, CL = 42.

11

• Задача 3. Дан Δ АВС , в котором угол В равен 30⁰, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D . Определите площадь треугольника ABD .

В

• Дано: ∆ АВС, ∠ ABC = 30 ⁰ BD – биссектриса АB = 4, BС = 6

Найти: S ABD

Решение:

4

6

А

С

D

3x

2x

• По свойству биссектрисы
• Пусть AD = 2 х ; DC = З х .

S ABD = AB ∙ AD ∙ sin A, S ABD =

S ABC = AB ∙ AC ∙ sin A, S ABC =

S ABC = AB ∙ BC ∙ sin B, S ABC = ∙ 4∙ 6 ∙ sin 30⁰ =6

=

S ABD = S ABC = ∙ 6 = 2,4

Ответ: 2,4

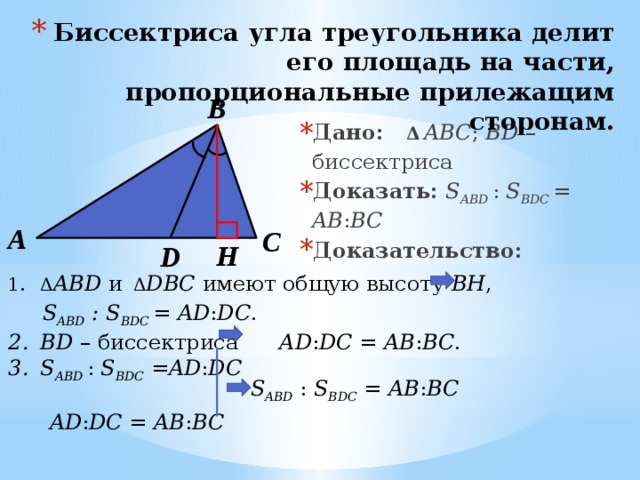
• Биссектриса угла треугольника делит его площадь на части, пропорциональные прилежащим сторонам.

В

• Дано:   Δ ABC ; BD – биссектриса
• Доказать:   S ABD   : S BDC   = AB : BC
• Доказательство:

А

С

H

D

• Δ ABD и  Δ DBC имеют общую высоту BH ,

S ABD  : S BDC   = AD : DC .

• BD – биссектриса AD : DC = AB : BC .
• S ABD   : S BDC  = AD : DC

AD : DC = AB : BC

S ABD  : S BDC  = AB : BC

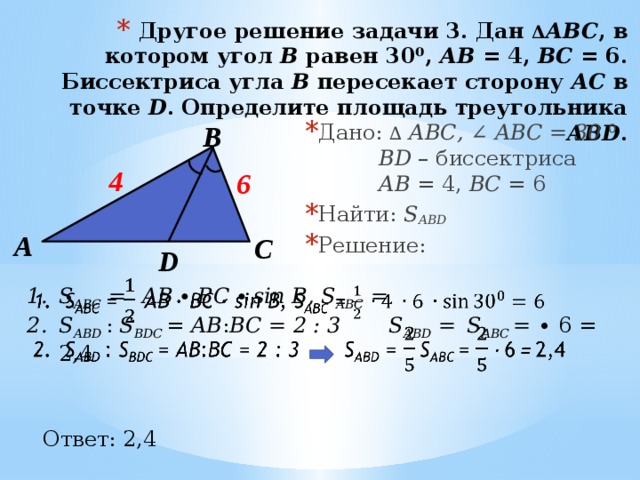
• Другое решение задачи 3. Дан Δ АВС , в котором угол В равен 30⁰, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D . Определите площадь треугольника ABD .

В

• Дано: ∆ АВС, ∠ ABC = 30 ⁰ BD – биссектриса АB = 4, BС = 6
• Найти: S ABD
• Решение:

4

6

А

С

D

• S ABC = AB ∙ BC ∙ sin B, S ABC =

• S ABD   : S BDC   = AВ : ВC = 2 : 3 S ABD = S ABC = ∙ 6 = 2,4

Ответ: 2,4

• Задача 4. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12.

B

Дано: Δ АВС, BD и AL – биссектрисы

BD ∩ AL = O, BО : OD = 3 : 2, АС = 12

Найти: Р АВС

Решение:

K

L

O

1. Из Δ ABD:

C

D

А

2. Из Δ CBD:

3.

+

4.

Ответ: 30

• Малоизвестные свойства биссектрисы треугольника

http:// math4school.ru/treugolniki.html#spr704

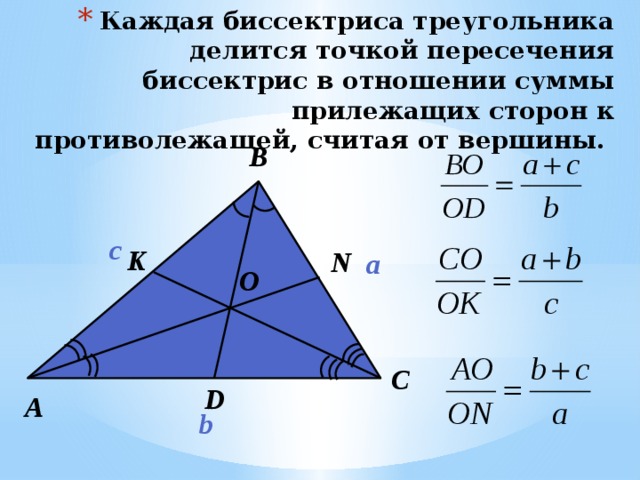
• Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.

B

с

K

N

a

O

C

D

А

b

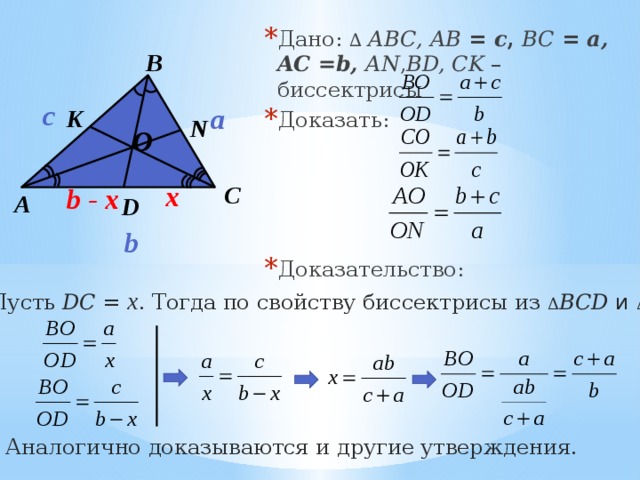
• Дано: ∆ АВС, AB = c , BC = a, AC =b, AN , BD, CK – биссектрисы
• Доказать:

• Доказательство:

B

с

a

K

N

O

x

C

b - x

А

D

b

1. Пусть DC = x . Тогда по свойству биссектрисы из Δ BCD и Δ ABD

2. Аналогично доказываются и другие утверждения.

• Другое решение задачи 4. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12.

B

• Дано: Δ АВС, BD и AL – биссектрисы

BD ∩ AL = O, BО : OD = 3 : 2, АС = 12

Найти: Р АВС

Решение:

L

О

А

С

D

Ответ: 30.

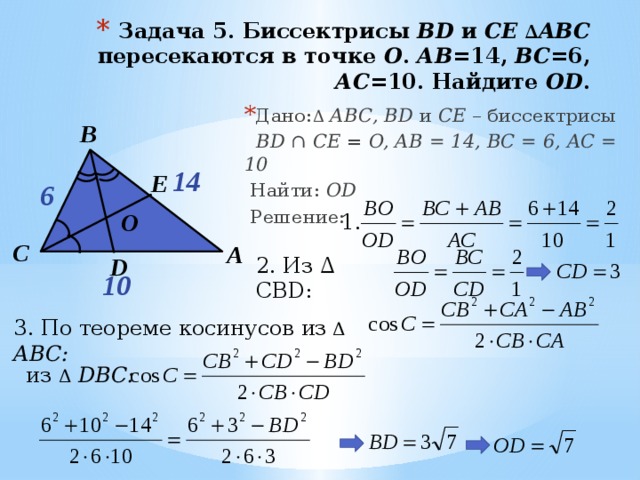
• Задача 5. Биссектрисы BD и CE ∆ ABC пересекаются в точке О . АВ =14, ВС =6, АС =10. Найдите ОD .

• Дано: Δ АВС, BD и CE – биссектрисы

BD ∩ CE = O, АB = 14, BC = 6, AC = 10

Найти: OD

Решение:

B

14

E

6

О

1.

C

A

D

2. Из ∆ CBD:

10

3. По теореме косинусов из Δ АВС:

из Δ DВС:

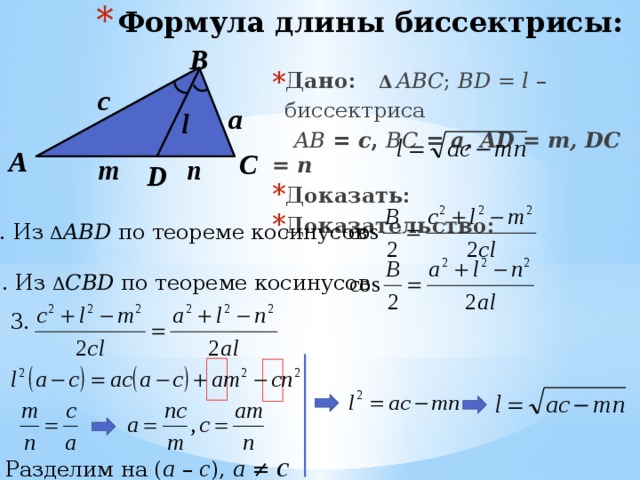
• Формула длины биссектрисы:

В

• Дано:   Δ ABC ; BD = l – биссектриса

AB = c , BC = a, AD = m, DC = n

• Доказать:  
• Доказательство:

с

a

l

А

С

m

n

D

1. Из Δ ABD по теореме косинусов

2. Из Δ СBD по теореме косинусов

3.

Разделим на ( а – с ), а ≠ с

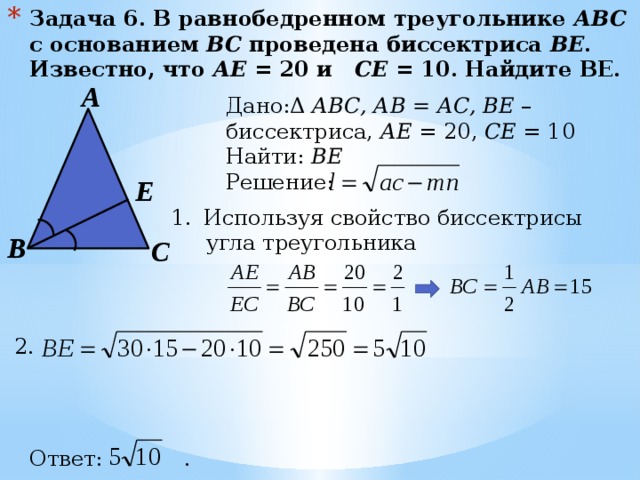
• Задача 6. В равнобедренном треугольнике АBC с основанием BС проведена биссектриса ВE . Известно, что АЕ = 20 и СE = 10. Найдите BE.

А

Дано:Δ АВС, АВ = АС, BE – биссектриса, АЕ = 20, СЕ = 10

Найти: ВЕ

Решение:

Е

• Используя свойство биссектрисы

угла треугольника

В

С

2.

Ответ: .

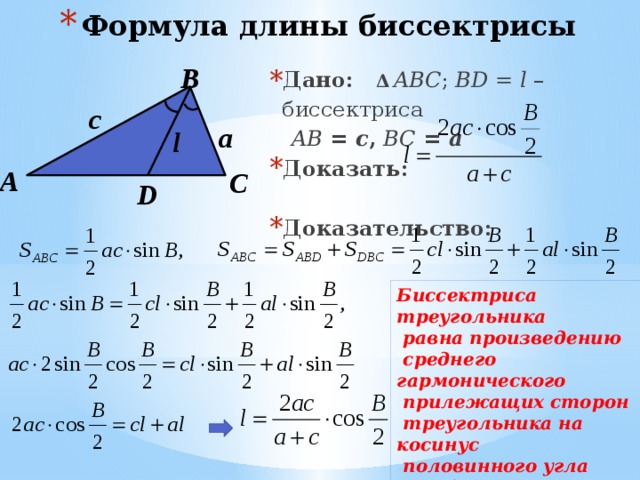
• Формула длины биссектрисы

В

• Дано:   Δ ABC ; BD = l – биссектриса

AB = c , BC = a

• Доказать:  

• Доказательство:

с

a

l

А

С

D

Биссектриса треугольника

равна произведению

среднего гармонического

прилежащих сторон

треугольника на косинус

половинного угла между ними.

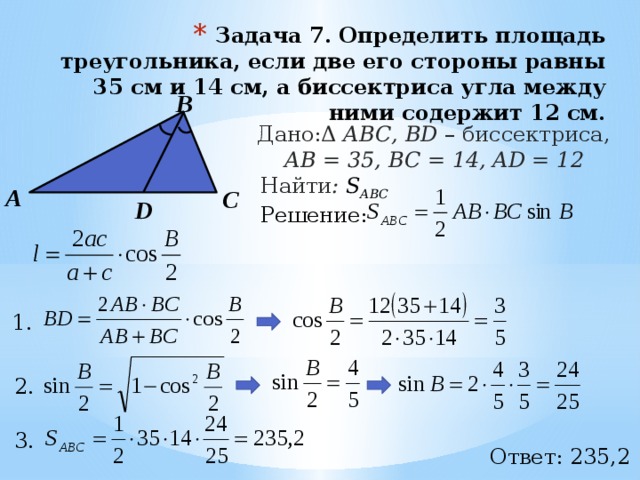
• Задача 7. Определить площадь треугольника, если две его стороны равны 35 см и 14 см, а биссектриса угла между ними содержит 12 см.

В

Дано:Δ АВС, BD – биссектриса, АB = 35, BC = 14, AD = 12

Найти : S АВС

Решение:

А

С

D

1.

2.

3.

Ответ: 235,2

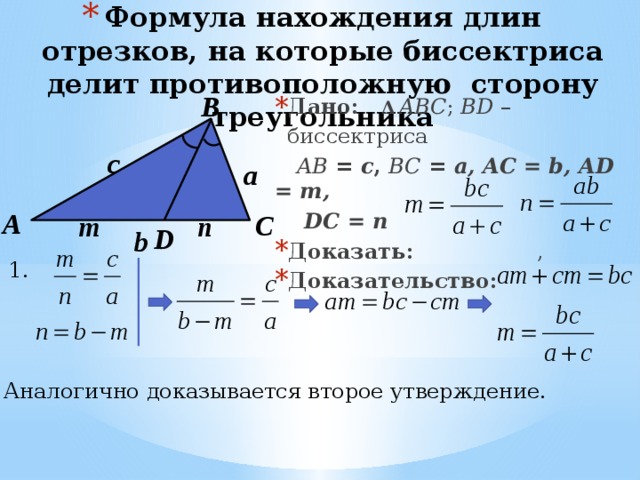
• Формула нахождения длин отрезков, на которые биссектриса делит противоположную сторону треугольника

В

• Дано:   Δ ABC ; BD – биссектриса

AB = c , BC = a, AC = b, AD = m,

DC = n

• Доказать:   ,
• Доказательство:

с

a

А

С

m

n

D

b

1.

2. Аналогично доказывается второе утверждение.

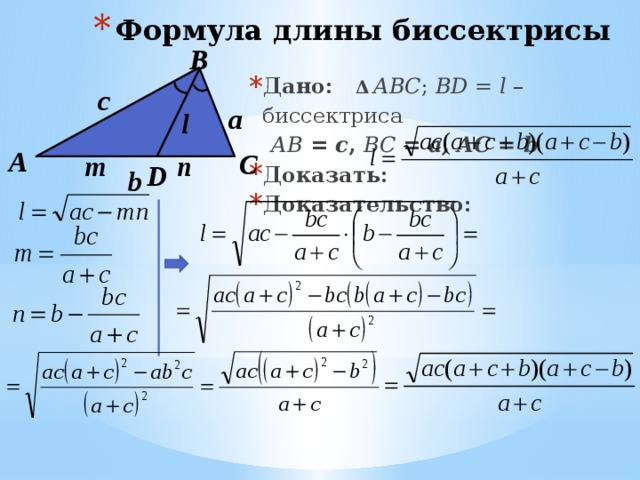
• Формула длины биссектрисы

В

• Дано:   Δ ABC ; BD = l – биссектриса

AB = c , BC = a, AC = b

• Доказать:  
• Доказательство:

с

a

l

А

С

n

m

D

b

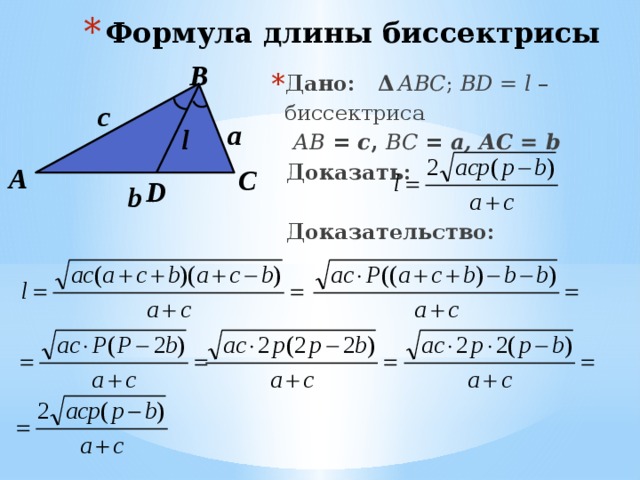
• Формула длины биссектрисы

В

• Дано:  Δ ABC ; BD = l – биссектриса

AB = c , BC = a, AC = b

Доказать:  

Доказательство:

с

a

l

А

С

D

b

• Другое решение задачи 5. Биссектрисы BD и CE ∆ ABC пересекаются в точке О . АВ =14, ВС =6, АС =10. Найдите ОD .

• Дано: Δ АВС, BD и CE – биссектрисы

BD ∩ CE = O, АB = 14, BC = 6, AC = 10

Найти: OD

Решение:

B

14

E

6

О

1.

C

A

2. Воспользуемся формулой

D

10

Ответ: .

• Медиана треугольника

• Что мы знаем о медиане треугольника из школьного учебника?

• Определение

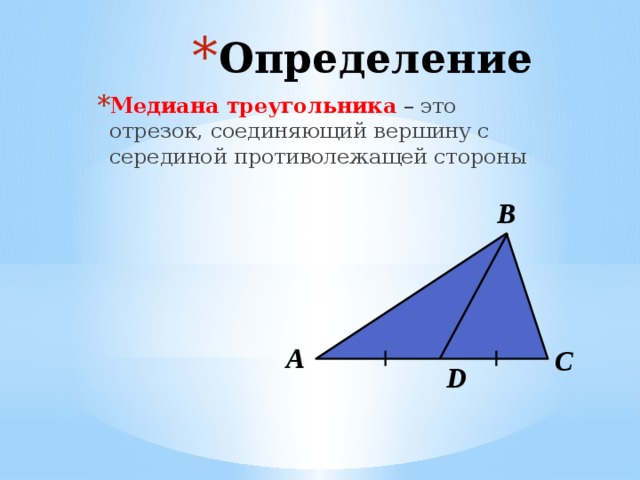
• Медиана треугольника  – это отрезок, соединяющий вершину с серединой противолежащей стороны

В

А

С

D

• Свойства медианы

В

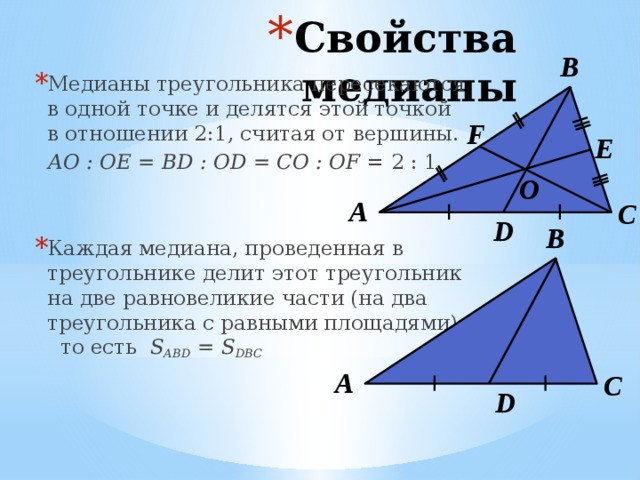
• Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

AO : OE = BD : OD = CO : OF = 2 : 1

• Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями), то есть  S ABD = S DBC

F

E

О

А

С

D

В

А

С

D

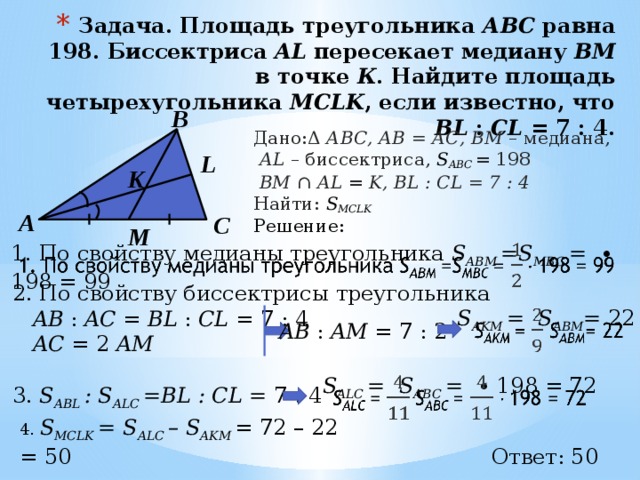
• Задача. Площадь треугольника АВС равна 198. Биссектриса AL пересекает медиану ВМ в точке К . Найдите площадь четырехугольника MCLK , если известно, что BL : CL = 7 : 4.

В

Дано:Δ АВС, АВ = АС, BМ – медиана,

АL – биссектриса, S ABC = 198

BM ∩ AL = K, BL : CL = 7 : 4

Найти: S MCLK

Решение:

L

K

А

С

M

1. По свойству медианы треугольника S ABM =S MBC = ∙ 198 = 99

2. По свойству биссектрисы треугольника

AB : AC = BL : CL = 7 : 4

AC = 2 AM

3. S ABL : S ALC =BL : CL = 7 : 4

S AKM = S ABM = 22

AB : AM = 7 : 2

S ALC = S ABC = ∙ 198 = 72

4. S MCLK = S ALC – S AKM = 72 – 22 = 50

Ответ: 50

• Малоизвестные свойства медианы треугольника

• Треугольник делится тремя медианами на шесть равновеликих треугольников.

В

• Дано: Δ АВС, AE, BD, CF, – медианы

Доказать:

S АOF = S АOD = S BOF = S BOE = S COE = S COD

Доказательство:

F

E

О

О

А

С

1. S АOD = S DOC , т.к. AD = DC и у этих треугольников общая высота, проведенная из вершины О .

D

Аналогично S AOF = S OFB, S BOE = S OEC

2. S АOD = АO ∙ OD ∙ sin AOD =

∙ AE ∙ BD ∙ sin AOD =

= ∙ AE ∙ BD ∙ sin AOD =

OE ∙ OB ∙sin BOE = S BOE

sin BOE

Аналогично получаем S AOF = S COE , S BOF = S COD.

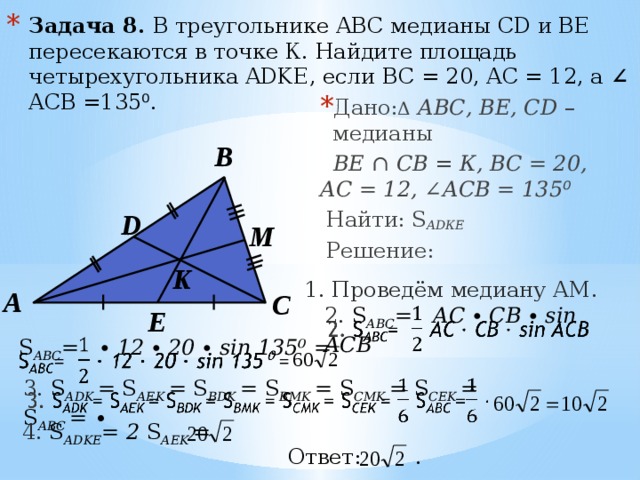
• Задача 8.  В треугольнике ABC медианы CD и BE пересекаются в точке К. Найдите площадь четырехугольника ADKE, если BC = 20, AC = 12, а ∠ ACB =135 ⁰ . 

• Дано: Δ АВС, BE, CD – медианы

BЕ ∩ CВ = К, ВС = 20, АC = 12, ∠ АСВ = 135 ⁰

Найти: S АDКЕ

Решение:

В

D

M

K

1. Проведём медиану АМ.

А

С

2. S АВС = АС ∙ СВ ∙ sin ACB

E

S АВС = ∙ 12 ∙ 20 ∙ sin 135⁰ =

3. S АDK = S АEK = S BDK = S BMK = S CMK = S CEK = S АВС = ∙

4. S АDKE = 2 S АEK =

Ответ: .

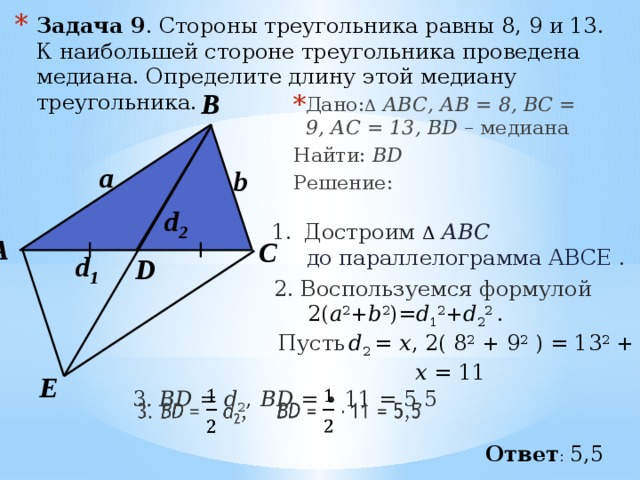
• Задача 9 . Стороны треугольника равны 8, 9 и 13. К наибольшей стороне треугольника проведена медиана. Определите длину этой медиану треугольника. 

В

• Дано: Δ АВС, АВ = 8, ВС = 9, АC = 13, BD – медиана

Найти: BD

Решение:

a

b

d 2

• Достроим Δ АВС

до параллелограмма АВСЕ .

А

С

d 1

D

2. Воспользуемся формулой

2( a 2 + b 2 )= d 1 2 + d 2 2 .

Пусть d 2 = х , 2( 8 2  + 9 2  ) = 13 2  + x 2

х = 11 

Е

BD = ∙ 11 = 5,5

3 . BD = d 2 ,

Ответ : 5,5

• Формула длины медианы через три стороны .

В

• Дано: Δ АВС, AB = c, BC = a, AC = b, BD = m b – медиана

Доказать:

Доказательство:

с

a

m b

π - α

α

А

С

D

• Воспользуемся теоремой косинусов

для Δ DВС и Δ АВD:

2. Сложим полученные равенства:

http:// www.resolventa.ru/spr/planimetry/mediana.htm

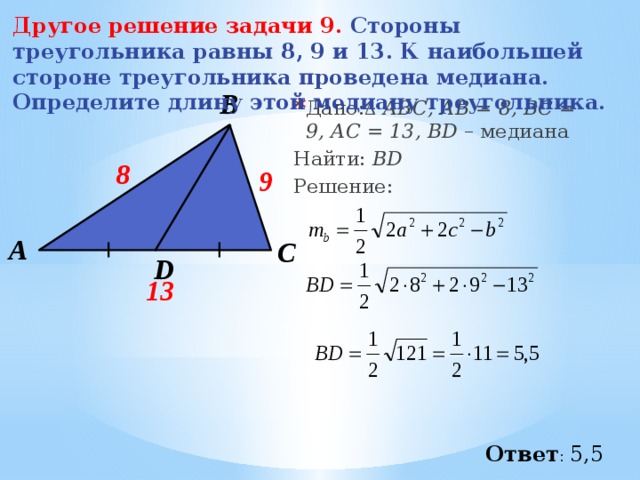
Другое решение задачи 9.  Стороны треугольника равны 8, 9 и 13. К наибольшей стороне треугольника проведена медиана. Определите длину этой медиану треугольника. 

В

• Дано: Δ АВС, АВ = 8, ВС = 9, АC = 13, BD – медиана

Найти: BD

Решение:

8

9

А

С

D

13

Ответ : 5,5

• Следствие. Длины медиан и длины сторон треугольника связаны формулой

В

• Дано: Δ АВС, AB = c, BC = a, AC = b, AM = m a , BE = m b, CD = m c – медианы

Доказать:

Доказательство:

D

M

K

А

С

E

+

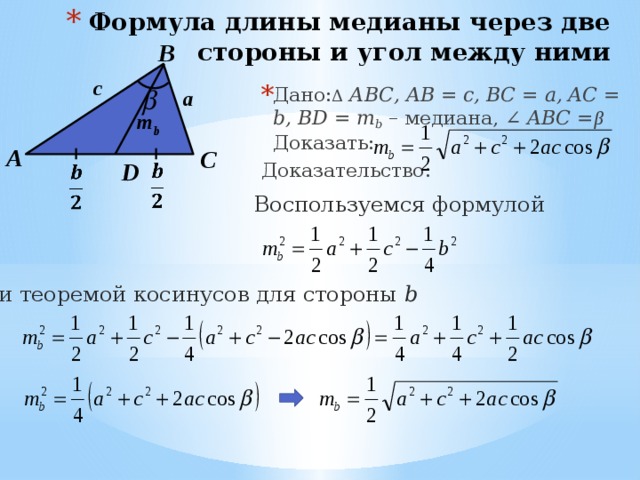
• Формула длины медианы через две стороны и угол между ними

В

с

• Дано: Δ АВС, AB = c, BC = a, AC = b, BD = m b – медиана, ∠ ABC = β Доказать:

Доказательство:

a

m b

А

С

D

Воспользуемся формулой

и теоремой косинусов для стороны b

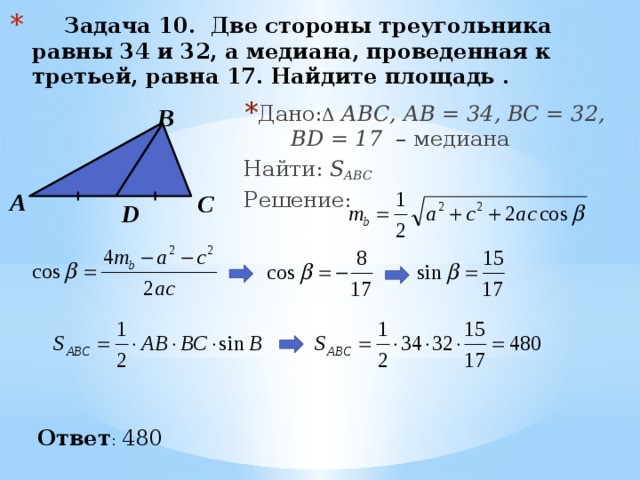
• Задача 10. Две стороны треугольника равны 34 и 32, а медиана, проведенная к третьей, равна 17. Найдите площадь .

• Дано: Δ АВС, АВ = 34, ВС = 32, BD = 17 – медиана

Найти: S ABC

Решение:

В

А

С

D

Ответ : 480

• Две стороны треугольника равны 6 и 8. Медианы, проведенные к серединам этих сторон, пересекаются под прямым углом.  Найти третью сторону треугольника.
• Периметр равнобедренного треугольника равен 16. Медиана, проведенная к боковой стороне, равна √17 . Найти стороны треугольника
• В треугольнике ABC точка K – середина медианы BM. Известно, что AB =7; BC = 5; AK = 6. Найти: CK.