Свойства дерева. Дерево случайного эксперимента

Дерево случайного эксперимента.

Пример 1

Рассмотрим хорошо знакомый нам эксперимент – двукратное броса­ние монеты. Начальное состояние, когда ни один бросок ещё не сделан, изобразим точкой S. При первом броске может выпасть орёл либо решка (смотрим на рисунке первое бросание). Изобразим эти два события точками О и Р и проведём к ним стрелки от точки S вниз влево и вправо. Стрелки будем называть рёбрами дерева. Начальная точка S, промежуточ­ные точки (О и Р) и конечные точки называются вершинами дерева.

Около рёбер напишем вероятности событий: ребро SO имеет вероятность и такую же вероятность имеет ребро SP.

Важно! При построении дерева нужно следить, чтобы сумма вероятностей око­ло всех рёбер, выходящих из одной вершины, была равна единице.

Проверим:

Пример 1 (продолжение)

Предположим сначала, что при первом броске выпал орёл. При втором броске то­же может выпасть орёл, и тогда наступит событие «два орла»: ОО. Вероятность вы­падения двух орлов равна Р(ОО) = . Но если в первый раз уже выпал орёл, то со­бытие ОО наступает с вероятностью – если во второй раз выпадет орёл. То есть условная вероятность двух орлов при условии, что в первый раз выпал орёл, равна Р(ОО|в 1 – й раз выпал орёл) = .

Аналогично для события «первый орел, вторая решка» Р(ОР|в 1 – й раз выпал орёл) = .

Рассмотрим правую ветвь нашего дерева.

Для события «первая решка, второй орел» Р(РО|в 1 – й раз выпала решка) = .

Для события «первая решка, вторая решка» Р(РР|в 1 – й раз выпала решка) = .

Пример 1 (продолжение)

Важно! Около ребер в дереве случайного опыта подписываются условные вероятности.

Если дерево случайного опыта конечное, то элементарные события в дереве случайного опыта изображаются цепями, ведущими из начальной вершины к конечным вершинам дерева.

Найти вероятность элементарного события можно с помощью правила умножения вероятностей: нужно найти произведение условных вероятностей вдоль соответствующей цепи.

Например, чтобы найти вероятность события ОР, нужно умножить вероятности вдоль цепи SOP: Р(ОР) = (на рисунке красная цепочка).

Важно! Чтобы найти вероятность события с помощью дерева, нужно сложить вероятности всех цепочек, ведущих к этому событию от начальной вершины.

Пример 3 (продолжение)

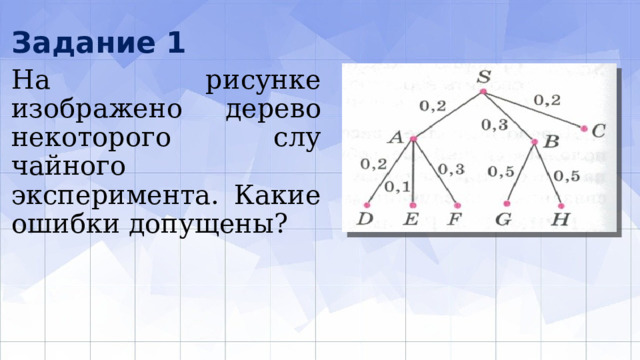
Задание 1

На рисунке изображено дерево некоторого слу­чайного эксперимента. Какие ошибки допущены?

Задание 2

На рисунке изображено дерево некоторого слу­чайного опыта.

а) Перерисуйте дерево в тетрадь и подпишите недо­стающие вероятности около рёбер.

б) Сколько элементарных событий в этом экспери­менте?

в) Пользуясь правилом умножения вероятностей, вычислите вероятности цепочек SAC и SBE.

г) Найдите вероятность события F.

Задание 3

На рисунке изображено дерево некоторого слу­чайного опыта и событие А. Рёбра проведены пунк­тиром. Известно, что из каждой точки возможные переходы к следующим событиям равновероятны.

а) Скопируйте рисунок в тетрадь и подпишите око­ло рёбер соответствующие вероятности.

б) Обведите сплошной линией цепочки, благоприятствующие событию А.

в) Найдите вероятность события А.

В

С

К

М

O

N

P

E

R

Домашнее задание:

1. На рисунке изображено дерево некоторого слу­чайного опыта.

а) Изобразите это дерево в своей тетради и подпи­шите недостающие вероятности около рёбер.

б) Вычислите вероятности цепочек SAC и SAGF.

2. На рисунке изображено дерево некоторого случайного опыта и показаны события А и В. Рёбра проведены пунктиром. Известно, что рёбра, исходящие из одной вершины, равновероятны.

а) Скопируйте рисунок в тетрадь. Обведите сплошной линией цепочки, бла­гоприятствующие событию А. Другим цветом обведите цепочки, благоприят­ствующие событию В

б) Найдите вероятность события А.

в) Найдите вероятность события В.