| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное АВТОНОМНОЕ образовательное учреждение высшего образования «Национальный исследовательский ядерный университет «МИФИ» |
| Московский областной политехнический колледж – филиал федерального государственного автономного образовательного учреждения высшего образования «Национальный исследовательский ядерный университет «МИФИ» (МОПК НИЯУ МИФИ) |
Методическое пособие для студентов
(Краткий курс лекций)
«Свойства тригонометрических функций.
Графики тригонометрических функций и их свойства»
Рассмотрено на заседании ПЦК
физико-математических дисциплин
Протокол № ____ от «____» ____________ 20___ г.
Председатель ЦК Л.А. Кувшинова_____________
Разработал преподаватель математики
Е.Н. Лебедева ______________________________
г. Электросталь 2022 г.
Пояснительная записка
Настоящее пособие предназначено для студентов как дневных, так и заочных отделений колледжа, а также может быть использовано для самостоятельного изучения темы, овладения способами и методами решения задач в объеме действующей программы по математике для средних профессиональных учебных заведений.
Целью и основными задачами данной разработки являются пополнение знаний студентов основами математических знаний, умений и навыков в объеме, необходимом для их повседневной практической деятельности, для дальнейшей учебы и работы по специальности, для усвоения общетехнических и специальных предметов, а также для дальнейшего повышения квалификации путем самообразования, обеспечение выпускнику конкурентоспособности на рынке труда.
Процесс изучения графиков тригонометрических функций и их свойств способствует развитию таких мыслительных операций, как анализ, синтез, обобщение. Знание рациональных приемов построения графиков необходимо будущему специалисту среднего специального звена.
Пособие содержит программный материал. В данном пособии весь теоретический материал изложен кратко и, поэтому доступен для большинства учащихся. Это способствует решению важной педагогической задачи – научить работать с источником.
В работе представлены теоретические сведения, необходимые для усвоения материала и решения задач.
Особенностью представленного пособия является усиление роли самостоятельной работы студентов.
Изучив, данное пособие студент должен уметь обобщать полученные знания, строить графики тригонометрических функций 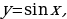
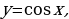
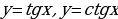 и описывать их свойства.
и описывать их свойства.
Свойства тригонометрических функций
Четность и нечетность функций
Определение. Функция 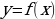 называется чётной, если для всех допустимых значений аргумента выполняется тождество
называется чётной, если для всех допустимых значений аргумента выполняется тождество
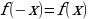
Определение. Функция 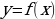 называется нечётной, если для всех допустимых значений аргумента выполняется тождество
называется нечётной, если для всех допустимых значений аргумента выполняется тождество
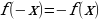
При построении графиков четных и нечетных функций удобно пользоваться следующими свойствами:
-
График четной функции симметричен относительно оси 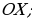
-
График нечетной функции симметричен относительно начала координат, т.е. относительно точки 
Рассмотрим вопрос о чётности и нечётности тригонометрических функций.
П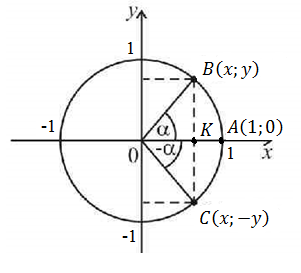 ри повороте на угол
ри повороте на угол  радиуса
радиуса  вокруг точки
вокруг точки 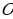 точка
точка 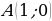 переходит в точку
переходит в точку 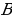 , а на угол
, а на угол 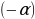 – в точку
– в точку 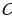 . Соединим точки
. Соединим точки 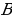 и
и 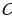 отрезком. Получим равнобедренный треугольник
отрезком. Получим равнобедренный треугольник 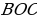 . Тогда
. Тогда 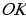 – медиана и, следовательно точки
– медиана и, следовательно точки 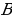 и
и 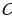 симметричны относительно оси
симметричны относительно оси 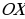 .
.
Если 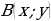 , то
, то 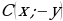 и, следовательно
и, следовательно
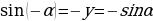
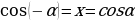
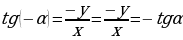
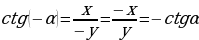
Вывод: Функция 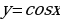 является чётной,
является чётной,
функции 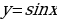 ,
, 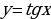 и
и 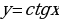 являются нечётными.
являются нечётными.
Периодичность функций
Функция 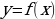 называется периодической с периодом
называется периодической с периодом 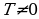 , если для каждой точки
, если для каждой точки 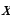 из её области определения точки
из её области определения точки 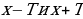 также принадлежат её области определения, и для них выполняется равенство
также принадлежат её области определения, и для них выполняется равенство
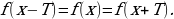
Для периодической функции справедливо также равенство
 где n – любое целое число.
где n – любое целое число.
Для построения периодических функций с периодом 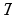 достаточно провести построение на отрезке длинной
достаточно провести построение на отрезке длинной 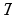 и затем перенести полученный график вдоль оси
и затем перенести полученный график вдоль оси 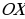 вправо и влево на расстояние
вправо и влево на расстояние 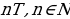 .
.
Все тригонометрические функции являются периодическими.
Теорема .1 Главный (наименьший) период функций 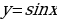 и
и 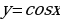 равен
равен 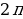 .
.
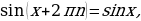
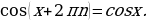
Теорема 2. Главный (наименьший) период функций 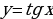 и
и 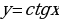 равен
равен 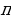 .
.
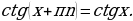
Графики тригонометрических функций и их свойства
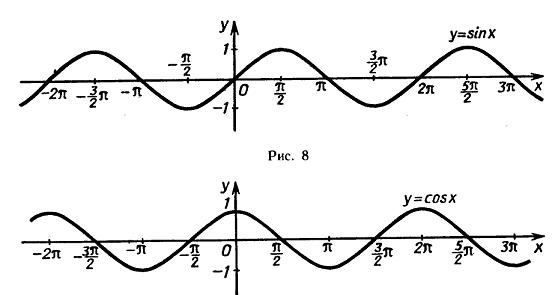
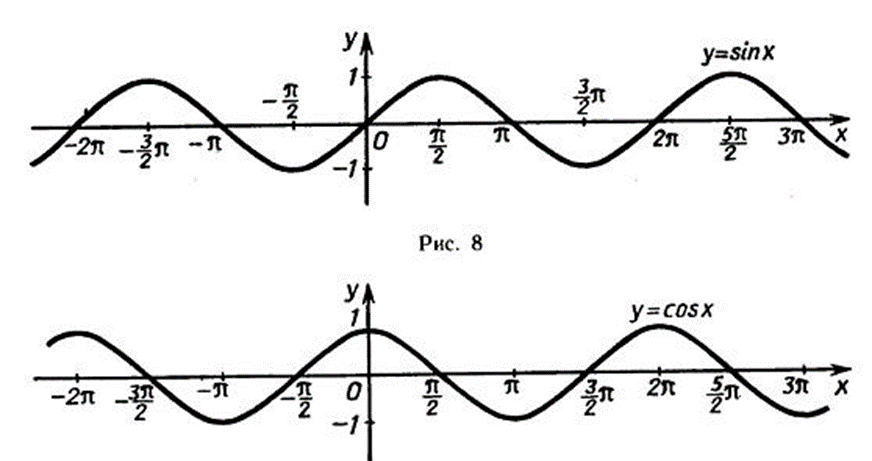
График функции 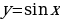
График функции называется синусоидой. Отрезок оси ординат 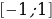 иногда называют линия синусов.
иногда называют линия синусов.
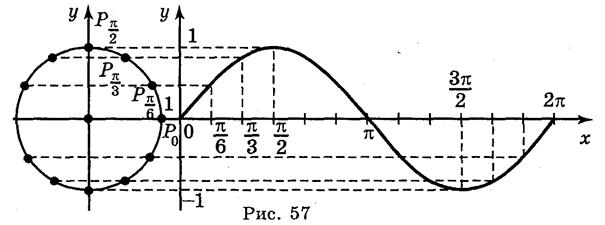
Построим график функции синус на отрезке 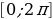 . Отметим на оси ординат точки
. Отметим на оси ординат точки 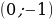 и
и 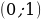 , а на оси абсцисс точку с абсциссой
, а на оси абсцисс точку с абсциссой 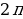 . Слева нарисуем единичную окружность.
. Слева нарисуем единичную окружность.
Теперь разделим единичную окружность и отрезок 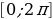 на 16 равных частей и воспользуемся определением синуса для построения ее графика. Отметим точку
на 16 равных частей и воспользуемся определением синуса для построения ее графика. Отметим точку 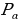 на единичной окружности и проведем через нее линию, параллельную оси абсцисс. Точка пересечения этой линии с прямой
на единичной окружности и проведем через нее линию, параллельную оси абсцисс. Точка пересечения этой линии с прямой 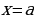 и есть искомая точка графика функции синуса. Ее ордината совпадает с ординатой точки
и есть искомая точка графика функции синуса. Ее ордината совпадает с ординатой точки 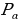 , а функция
, а функция 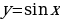 по определению и есть ордината точки
по определению и есть ордината точки  .
.
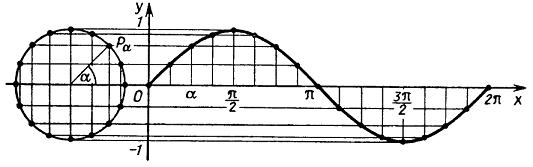
Для продолжения графика по оси  дальше, чем точка
дальше, чем точка  , необходимо воспользоваться свойством периодичности функции
, необходимо воспользоваться свойством периодичности функции 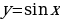 :
: 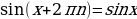 , где
, где 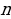 – целое число. Таким образом, график синуса на всей числовой прямой получается путем параллельного переноса его части на отрезке
– целое число. Таким образом, график синуса на всей числовой прямой получается путем параллельного переноса его части на отрезке 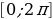 вдоль оси
вдоль оси 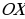 на
на 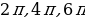 , и т.д.
, и т.д.
Свойства:
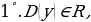
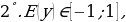
3°. Функция нечётная, т.к. 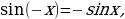 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат,
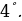 Функция периодическая с
Функция периодическая с 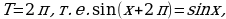
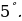 Интервалы монотонности:
Интервалы монотонности:
функция возрастает при 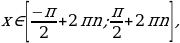
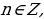
функция убывает при 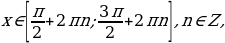
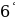 . Промежутки знакопостоянства:
. Промежутки знакопостоянства:
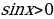 при
при 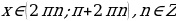
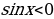 при
при 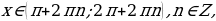
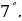 Наибольшее и наименьшее значение функции:
Наибольшее и наименьшее значение функции:
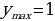 при
при 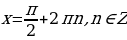 ,
,
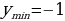 при
при 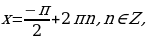
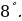 Точки пересечения с осями координат:
Точки пересечения с осями координат:
c осью 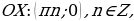
с осью 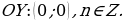
График функции 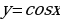
График функции называется косинусоида. Чаще график функции косинуса так же называется синусоидой.
Для построения графика функции 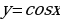 воспользуемся формулой приведения:
воспользуемся формулой приведения: 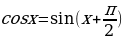 . Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на
. Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на  в отрицательном направлении оси абсцисс.
в отрицательном направлении оси абсцисс.
Свойства:
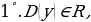
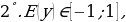
3°. Функция чётная, т.к. 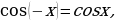 т.е. график симметричен относительно оси
т.е. график симметричен относительно оси 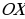 ,
,
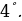 Функция периодическая с
Функция периодическая с 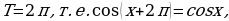
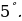 Интервалы монотонности:
Интервалы монотонности:
Функция возрастает при 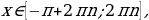
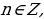
функция убывает при 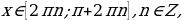
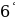 . Промежутки знакопостоянства:
. Промежутки знакопостоянства:
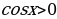 при
при 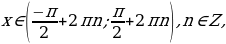
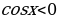 при
при 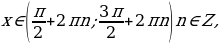
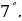 Наибольшее и наименьшее значение функции:
Наибольшее и наименьшее значение функции:
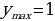 при
при 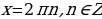 ,
,
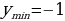 при
при 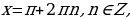
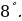 Точки пересечения с осями координат:
Точки пересечения с осями координат:
c осью 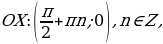
с осью 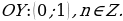
График функции 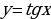
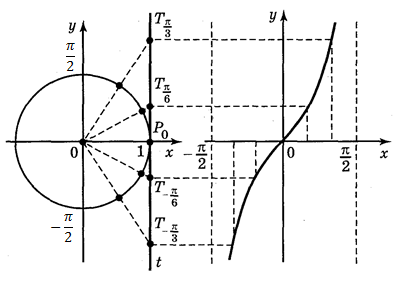
График функции называется тангенсоида.
Построение графика 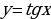 на интервале
на интервале 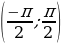 аналогичен построению, описанному в случае синуса. (Значение функции
аналогичен построению, описанному в случае синуса. (Значение функции 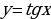 находят с помощью линии тангенса).
находят с помощью линии тангенса).
Из рисунка видно, что в точках 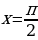 и
и 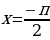 функция
функция 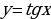 не определена, следовательно в этих точках проходят асимптоты графика.
не определена, следовательно в этих точках проходят асимптоты графика.
Определение. Асимптота – прямая, к которой неограниченно приближается точка некоторой кривой по мере того, как она удаляется в бесконечность.
И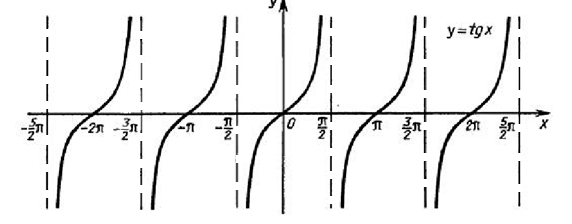 спользуя периодичность, построить график функции
спользуя периодичность, построить график функции 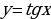 на всей области определения.
на всей области определения.
Свойства:
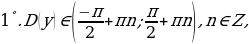
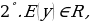
3°. Функция нечётная, т.к. 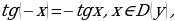 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат,
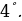 Функция периодическая с
Функция периодическая с 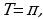 т.е.
т.е. 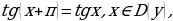
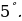 Интервалы монотонности:
Интервалы монотонности:
Функция возрастает при 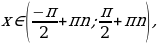
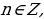
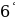 . Промежутки знакопостоянства:
. Промежутки знакопостоянства:
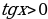 при
при 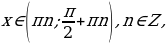
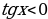 при
при 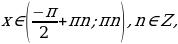
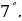 Наибольшего и наименьшего значения функция не имеет,
Наибольшего и наименьшего значения функция не имеет,
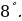 Асимптоты:
Асимптоты: 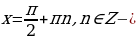 вертикальная асимптота,
вертикальная асимптота,
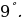 Точки пересечения с осями координат:
Точки пересечения с осями координат:
с осью 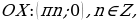
с осью 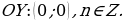
График функции 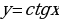
График функции называется котангенсоида.
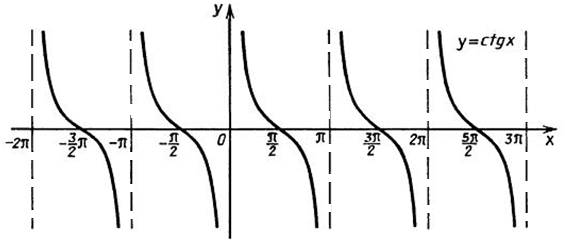
Свойства:
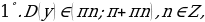
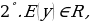
3°. Функция нечётная, т.к. 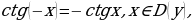 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат,
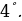 Функция периодическая с
Функция периодическая с 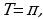 т.е.
т.е. 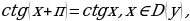
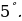 Интервалы монотонности:
Интервалы монотонности:
Функция убывает при 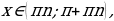
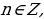
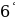 . Промежутки знакопостоянства:
. Промежутки знакопостоянства:
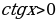 при
при 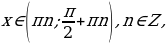
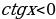 при
при 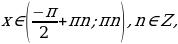
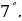 Наибольшего и наименьшего значения функция не имеет,
Наибольшего и наименьшего значения функция не имеет,
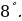 Асимптоты:
Асимптоты: 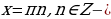 вертикальная асимптота,
вертикальная асимптота,
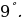 Точки пересечения с осями координат:
Точки пересечения с осями координат:
с осью 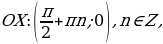
с осью 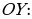 нет.
нет.
Рекомендуемая литература
Богомолов Н.В. Математика: учеб. для ссузов – М.: Дрофа, 2015.
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер. – СПб.: Петроглиф, 2017.







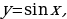
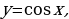
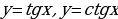 и описывать их свойства.
и описывать их свойства.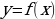 называется чётной, если для всех допустимых значений аргумента выполняется тождество
называется чётной, если для всех допустимых значений аргумента выполняется тождество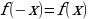
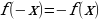
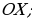
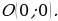
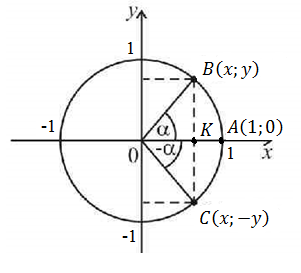 ри повороте на угол
ри повороте на угол 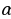 радиуса
радиуса 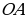 вокруг точки
вокруг точки 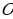 точка
точка 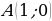 переходит в точку
переходит в точку 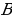 , а на угол
, а на угол 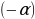 – в точку
– в точку 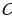 . Соединим точки
. Соединим точки 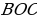 . Тогда
. Тогда 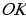 – медиана и, следовательно точки
– медиана и, следовательно точки 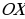 .
.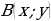 , то
, то 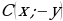 и, следовательно
и, следовательно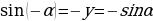
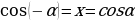
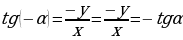
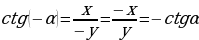
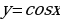 является чётной,
является чётной, 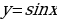 ,
, 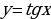 и
и 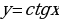 являются нечётными.
являются нечётными.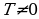 , если для каждой точки
, если для каждой точки 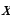 из её области определения точки
из её области определения точки 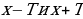 также принадлежат её области определения, и для них выполняется равенство
также принадлежат её области определения, и для них выполняется равенство 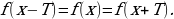
 где n – любое целое число.
где n – любое целое число.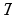 достаточно провести построение на отрезке длинной
достаточно провести построение на отрезке длинной 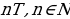 .
.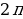 .
.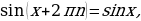
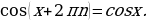
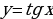 и
и 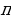 .
.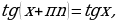
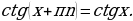
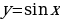
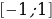 иногда называют линия синусов.
иногда называют линия синусов.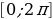 . Отметим на оси ординат точки
. Отметим на оси ординат точки 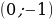 и
и 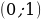 , а на оси абсцисс точку с абсциссой
, а на оси абсцисс точку с абсциссой 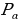 на единичной окружности и проведем через нее линию, параллельную оси абсцисс. Точка пересечения этой линии с прямой
на единичной окружности и проведем через нее линию, параллельную оси абсцисс. Точка пересечения этой линии с прямой 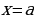 и есть искомая точка графика функции синуса. Ее ордината совпадает с ординатой точки
и есть искомая точка графика функции синуса. Ее ордината совпадает с ординатой точки 
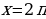 , необходимо воспользоваться свойством периодичности функции
, необходимо воспользоваться свойством периодичности функции 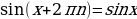 , где
, где 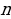 – целое число. Таким образом, график синуса на всей числовой прямой получается путем параллельного переноса его части на отрезке
– целое число. Таким образом, график синуса на всей числовой прямой получается путем параллельного переноса его части на отрезке 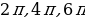 , и т.д.
, и т.д.

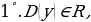
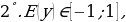
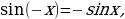 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат, 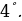 Функция периодическая с
Функция периодическая с 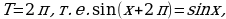
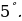 Интервалы монотонности:
Интервалы монотонности: 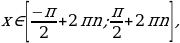
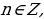
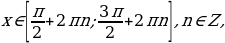
 . Промежутки знакопостоянства:
. Промежутки знакопостоянства: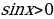 при
при 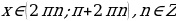
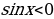 при
при 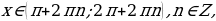
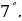 Наибольшее и наименьшее значение функции:
Наибольшее и наименьшее значение функции: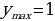 при
при 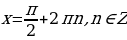 ,
,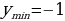 при
при 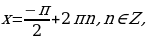
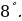 Точки пересечения с осями координат:
Точки пересечения с осями координат: 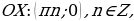
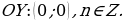
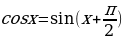 . Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на
. Следовательно, график функции косинуса получается из графика синуса путем его параллельного переноса на  в отрицательном направлении оси абсцисс.
в отрицательном направлении оси абсцисс.
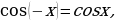 т.е. график симметричен относительно оси
т.е. график симметричен относительно оси 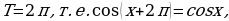
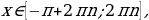
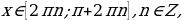
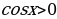 при
при 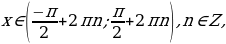
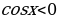 при
при 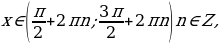
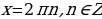 ,
,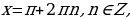
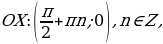
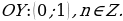
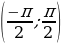 аналогичен построению, описанному в случае синуса. (Значение функции
аналогичен построению, описанному в случае синуса. (Значение функции 
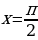 и
и 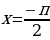 функция
функция  спользуя периодичность, построить график функции
спользуя периодичность, построить график функции 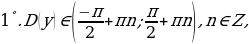
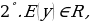
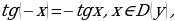 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат, 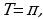 т.е.
т.е. 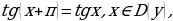
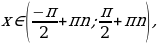
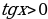 при
при 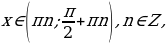
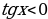 при
при 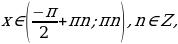
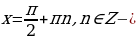 вертикальная асимптота,
вертикальная асимптота,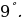 Точки пересечения с осями координат:
Точки пересечения с осями координат: 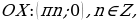

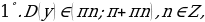
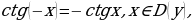 т.е. график симметричен относительно начала координат,
т.е. график симметричен относительно начала координат, 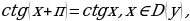
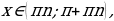
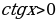 при
при 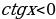 при
при 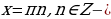 вертикальная асимптота,
вертикальная асимптота,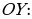 нет.
нет.



















