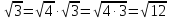Тема урока « Свойства квадратных корней».( 8 класс)
Учитель математики Цомаева Ирина Владимировна.
Тип урока –комбинированный.
Цель:
обобщить и систематизировать умения и навыки учащихся по преобразованию выражений , содержащих квадратные корни.
Задачи:
изучить свойства квадратных корней;
применение свойств корней при нахождении значений выражений, содержащего корень из произведения и частного;
внесение множителя под корень и вынесение множителя из - под корня.
развивать познавательную активность учащихся;
воспроизведение изученной информации.
воспитание культуры математического письма и речи;
воспитание логического мышления, ответственности за получение знаний;
формирование информационной коммуникативности.
Оборудование:
экран, проектор, карточки для самостоятельной работы.
ХОД УРОКА.
1. Организационный момент.
Сообщение темы урока.
Учитель Ребята, сегодня у нас необычный урок, в гостях у нас учителя школы, покажем им свои знания. Девизом нашего урока служит китайская мудрость: « Я слышу- я забываю Я вижу – я запоминаю Я делаю – я усваиваю». Ребята, сегодня мы изучим с вами свойства квадратных корней, а также научимся применять их при преобразованиях выражений, содержащих корни.
На сегодня вам были заданы номера № 260, № 263,№ 302. Возникли ли у вас вопросы по заданным пунктам?
Передайте тетради с домашними заданиями.
2. Актуализация опорных знаний.( мотивация учащихся)
( в ходе устной работы ставится проблема, которая будет решена при изучении новой темы)
Ребята при выполнении заданий домашней работы перед вами ставились задачи . Попробуем выяснить для себя насколько точны ваши действия.
Перед вами задания ( слайды 2 -3):
Ответим на них:
1. Что мы называем квадратным корнем?
Ответ: Квадратным корнем из числа b называется такое число квадрат , которого равен b .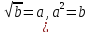 ).
).
2.Найдите квадратные корни числа: 
3.Найдите значение выражения
 .
.
4. Как читается выражение 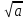 ? При каких значениях переменной a выражение имеет смысл? (« корень квадратный из a » , при a ≥ 0)
? При каких значениях переменной a выражение имеет смысл? (« корень квадратный из a » , при a ≥ 0)
5. При каких значениях а выполняется равенство ( при a ≥0)
( при a ≥0)
6. Сравните : и 5 б) 2
и 5 б) 2 ?
?
Чтобы мы смогли сравнивать числа вида 2 , мы должны изучить свойства квадратных корней.
, мы должны изучить свойства квадратных корней.
3. Изучение новой темы.( слайды 4 -9).
1 Найдите значения выражений : 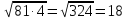 ,
,
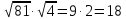 .
.
Вывод: 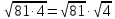 .
.
Запишем в тетрадях алгебраическое равенство, выражающее данное свойство.

Теорема. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Выполним задания на применения данного свойства. К доске выходит ученик( слайд 5)
Вычислите :
1) 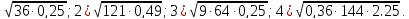
2. Найдите значения выражений: ( слайд 6) 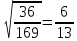 ;
;
 .
.
Вывод :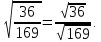
Запишем алгебраическое равенство , выражающее данное свойство.
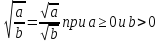
Теорема. Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Выполним задания на закрепление данного свойства. Выходит ученик к доске ( слайд 7)
Вычислите :
1)
Еще я покажу свойство, позволяющее удобно вычислять квадратные корни из степеней, с четными показателями.
Вам хорошо известно свойство  =a при a≥0 ,
=a при a≥0 ,
тогда  .
.
Ученик выходит к доске для закрепления данного свойства
Вычислите и упростите:
1)
Изученные нами сегодня свойства позволяют преобразовывать выражения, содержащие корни.( слайд 8)
Например, ранее считалось , что число  иррациональное, но если число 12 представить в виде произведения 3· 4 , тогда
иррациональное, но если число 12 представить в виде произведения 3· 4 , тогда

Таким образом , мы вынесли множитель из – под корня.
В случаях, когда нам необходимо сравнивать числа вида 2 , нам необходимо внести множитель под знак корня. ( слайд 9)
, нам необходимо внести множитель под знак корня. ( слайд 9)
Например,
2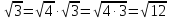
Вносить отрицательное число под знак корня нельзя!
4. Закрепление ( слайд 10 -11)
На доске записаны задания на закрепление.
1. Вынести множитель из – под корня :
1) .
.
2. Внести множитель под знак корня:
1) ; 3)
; 3) .
.
3. Сравните :
1) .
5. Рефлексия.( слайд 12).
Самостоятельная работа в 5 вариантах.
Решения записываются в ячейках.
Дети выделяют для себя пункты , вызывающие у них затруднения; степень усвоения нового материала, осуществляют самоконтроль.
6.Подведение итогов.
Историческая справка.
Мы повторили с вами теоретический материал, а откуда же появился этот необычный знак обозначающий корень квадратный и для этого мы с вами отправимся на планету истории.
О ЗНАКЕ КОРНЯ. Начиная с 13 века итальянские и другие европейские математики обозначали корень латинским словом Radix (корень) или сокращенно Rх. В 15 веке писали R212 вместо  .
.
В 1626 году нидерландский математик А.Ширар ввел близкое к современному обозначение корня V. Если над этим знаком стояла цифра 2, то это означало корень квадратный.
Это обозначение стало вытеснять знак Rх. Однако долгое время писали V а +в с горизонтальной чертой над суммой. Лишь в 1637 году Рене Декарт соединил знак корня с горизонтальной чертой, применив в своей “Геометрии” современный знак корня  . Этот знак вошел во всеобщее употребление лишь в начале 18 века.
. Этот знак вошел во всеобщее употребление лишь в начале 18 века.
Знак корня был введен практической необходимостью, зная площадь людям в 16 веке нужно было вычислять сторону квадрата. Для этого был введен корень квадратный.
7. Задание на дом
стр 81 п.2.6,
№ 321,№ 323, № 336, № 339.
Самостоятельная работа. Тема «Свойства квадратных корней»
| № | 1вариант | 2вариант | 3вариант | 4вариант | 5вариант |
| 1 | 
| 
| 
| 
| 
|
| 2 | 
| 
| 
| 
| 
|
| 3 | 
| 
| 
| 
| 
|
| 4 | 
| 
| 
| 
| 
|
| 5 | 
| 
| 
| 
| 
|
| 6 | 
| 
| 
| 
| 
|
| 7 | 
| 
| 
| 
| 
|
| 8 | 
| 
|  
| 
| 
|
| 9 | 
| 
| 
| 
| 
|
| 10 | 
| 
| 
| 
| 
|
| 11 | 
| 
| 
| 
| 
|
| 12 | 
| 
| 
| 
| 
|
| 13 | 
| 
| 
| 
| 
|
| 14 | 
| 
| 
| 
| 
|
| 15 | 
| 
| 
| 
| 
|
| 16 | 
| 
| 
| 
| 

|
| 17 | 
| 
| 
| 
| 
|
| 18 | 
| 
|  
| 
| 
|
| 19 | 
| 
| 
| 
| 
|
| 20 | 
| 
|  
| 
| 
|







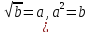 ).
).
 .
.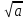 ? При каких значениях переменной a выражение имеет смысл? (« корень квадратный из a » , при a ≥ 0)
? При каких значениях переменной a выражение имеет смысл? (« корень квадратный из a » , при a ≥ 0) ( при a ≥0)
( при a ≥0) и 5 б) 2
и 5 б) 2 ?
?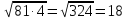 ,
,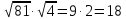 .
.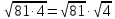 .
.
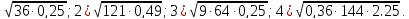
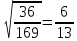 ;
;  .
.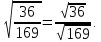
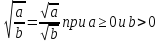

 =a при a≥0 ,
=a при a≥0 , .
.
 иррациональное, но если число 12 представить в виде произведения 3· 4 , тогда
иррациональное, но если число 12 представить в виде произведения 3· 4 , тогда