Свойства серединного перпендикуляра к отрезку

Дата: 02.04.2020

Тема: СВОЙСТВА СЕРЕДИННОГО ПЕРПЕНДИКУЛЯРА К ОТРЕЗКУ

Задачи: ввести понятие серединного перпендикуляра к отрезку; рассмотреть теорему о серединном перпендикуляре и следствия из неё, закрепить полученные знания в ходе решения задач.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Выполните устно предложенные задачи.

У вас должны получиться ответы: 144; CBE; 117; 41.

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Откройте свои тетради и запишите сегодняшнее число и тему. Выполните конспект, приведенный ниже.

Определение. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

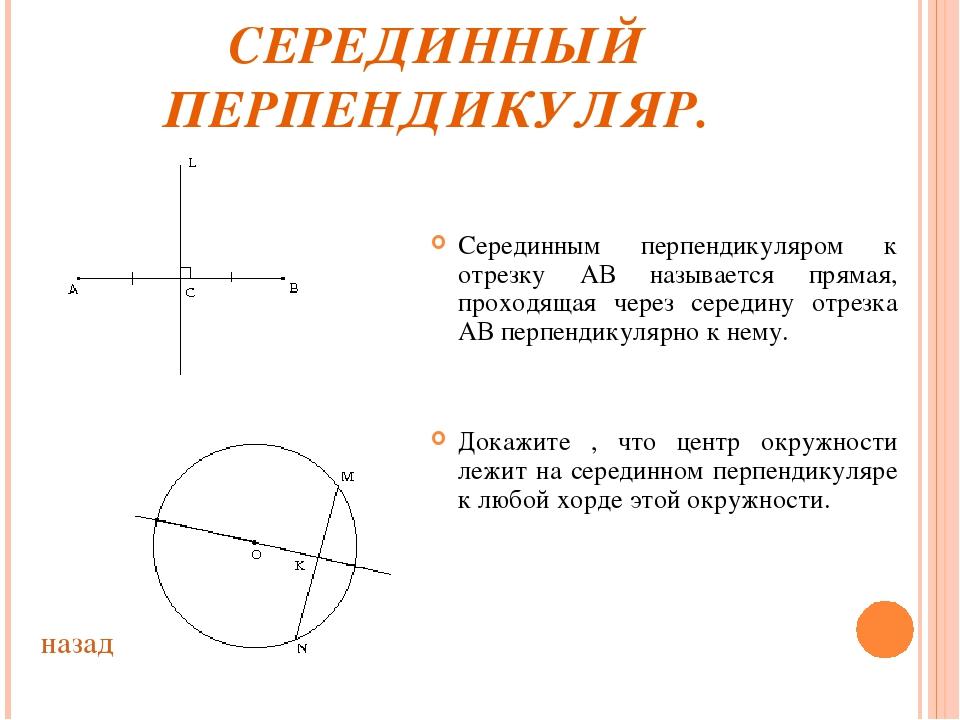
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. (MA=MB)

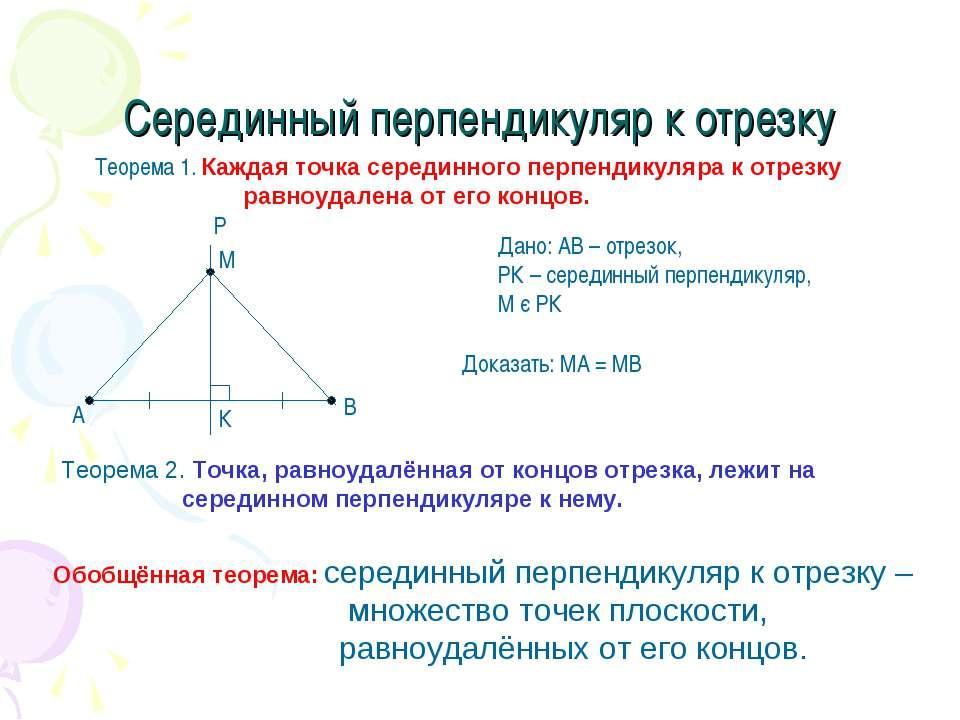
Обратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Следствие 1. Геометрическим местом точек плоскости, равноудаленных от концов отрезка, является серединный перпендикуляр этому отрезку.

Следствие 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Откройте учебники на странице 177 и выполним все вместе № 679. Прочтите внимательно условие задачи. Давайте выполним рисунок и оформим краткую запись к задаче.

№679

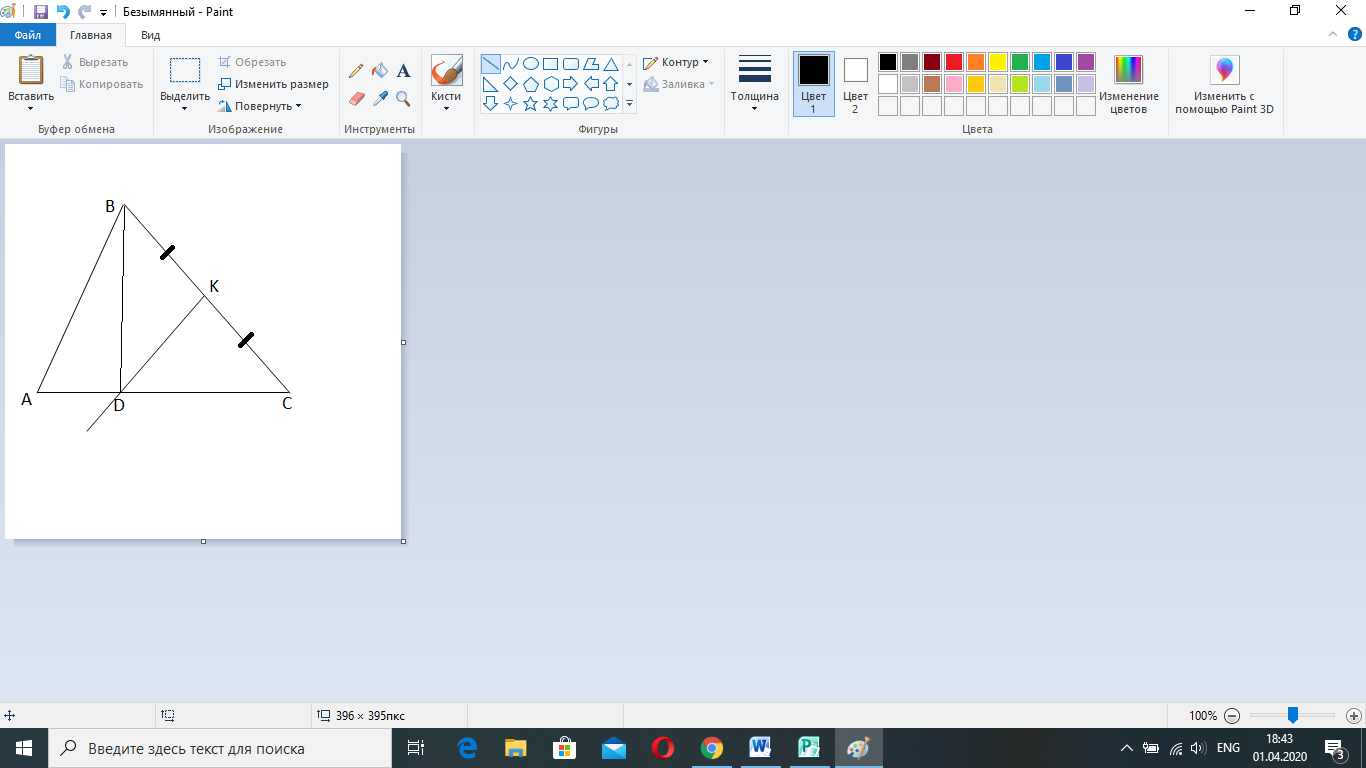
Дано: ∆АВС, DK – серединный перпендикуляр, DK⊥ ВС.

а) BD=5 см, АС=8,5 см;

б) BD=11,4 см, АD=3,2 см.

Найти: а) АD и СD; б) АС.

Решение: Т.к. DK – серединный перпендикуляр, то BD=DC (по теореме).

а) BD=DC=5 см.

АD=АС- DC=8,5-5=3,5 см.

б) BD=DC=11,4 см.

АС= АD+ DC=11,4+3,2=14,6 см.

Ответ: а) 5 см и 3,5 см; б) 14,6 см.

Надеюсь, вы разобрались в решении. Выполните самостоятельно №681. Если возникнут вопросы, я готова ответить и подсказать.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Какую теорему сегодня изучили? Какие следствия из теоремы запомнили?

Д омашнее задание: выучить теорию + задачи.

Задача 1.

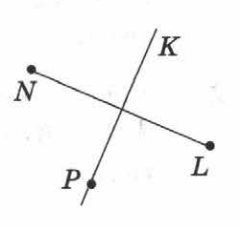
Задача 2.