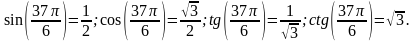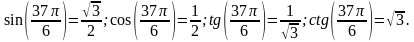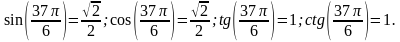Просмотр содержимого документа
«Свойства тригонометрический функций.»
Свойства синуса и косинуса. Свойства тангенса и котангенса.
Подпишите работу
ФИО _______________________________________________________ класс_______________
З адание: Изучите теоретический материал. Разберите приведенные примеры задач по теме. Выполните задание для самостоятельного решения.
адание: Изучите теоретический материал. Разберите приведенные примеры задач по теме. Выполните задание для самостоятельного решения.
Знаки тригонометрических функций по четвертям
|
| I | II | III | IV |
| cos α | + | − | − | + |
| sin α | + | + | − | − |
| tg α | + | − | + | − |
| ctg α | + | − | + | − |
ВАЖНО: Углы ±90°, ±180°, ±270°, ±360 не принадлежат ни одной четверти, так как лежат на координатных осях.
Выучите свойства периодичности и свойства противоположных углов тригонометрических функций.
Свойство (периодичности): При изменении угла на целое число полных оборотов (2π) значения синуса, косинуса, тангенса и котангенса остаются неизменными.
М![]() атематически данное свойство записывается так:
атематически данное свойство записывается так:
sin(α+2π∙z)=sin α
cos(α+2π∙z)=cos α
tg(α+2π∙z)=tg α
ctg(α+2π∙z)=ctg α, где z – целое число.
Свойства (синусов, косинусов, тангенсов и котангенсов противоположных углов):
1. sin (−α) = −sin α
2. cos (−α) = cos α
3. tg (−α) = −tg α
4. ctg (−α) = −ctg α
Тщательно проанализируйте решение приведенной задачи:
Пример 1.
Вычислите значения синуса, косинуса, тангенса и котангенса при 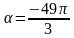 .
.
Решение:
Числам α и (α + 2πk), k – целое число, соответствует одна точка числовой окружности, то:
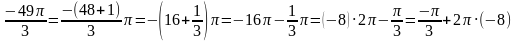
Воспользуемся свойством периодичности тригонометрических функций:
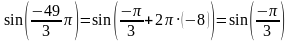
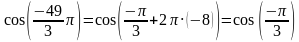
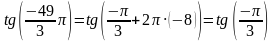
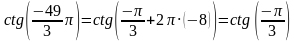
Из таблицы значений тригонометрических функций получаем:
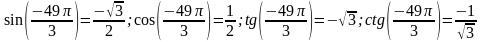
Задание для самостоятельного решения:
На отдельном листочке решите задачу. Обведите в кружок правильный вариант ответа.
Вычислите значения синуса, косинуса, тангенса и котангенса при 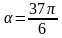 .
.
а) 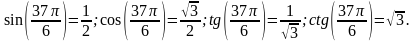
б) 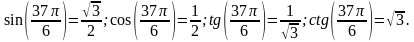
в) 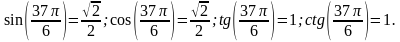
г) 






 адание: Изучите теоретический материал. Разберите приведенные примеры задач по теме. Выполните задание для самостоятельного решения.
адание: Изучите теоретический материал. Разберите приведенные примеры задач по теме. Выполните задание для самостоятельного решения.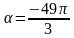 .
.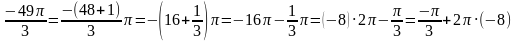
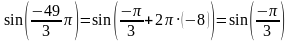
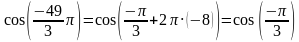
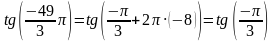
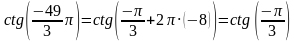
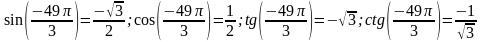
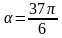 .
.